算法中逐位统计的二进制思想

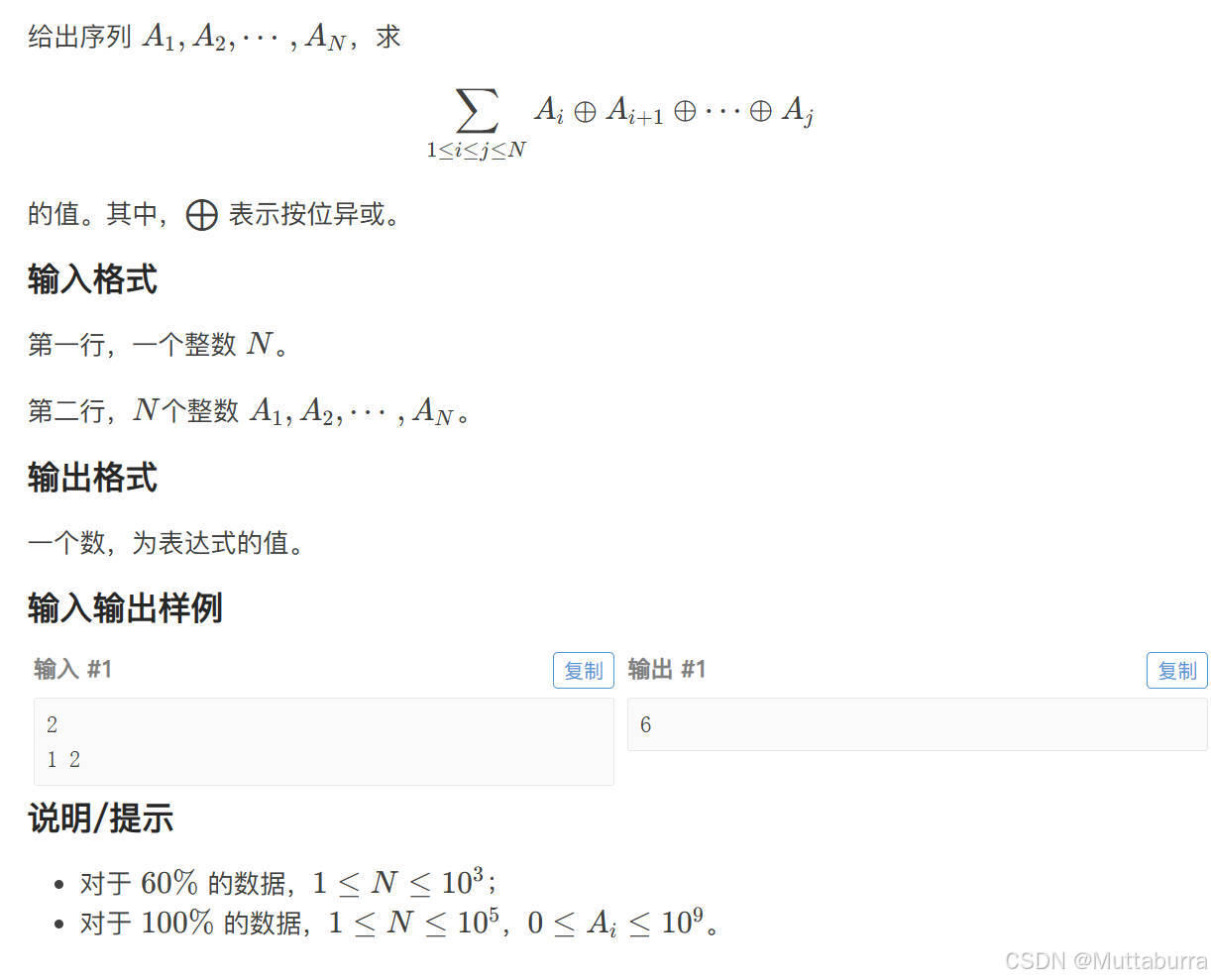
题目：

前置知识：

首先看到区间异或计算，很容易想到我们可以用前缀和优化，因为异或计算具有可逆性，那么我们就可以把复杂度降低到，但是显然对于1e5的数据范围依然过高，那么在这里我们需要用到逐位统计的二进制思想。

从数据范围我们可以看出，异或结果不会爆int，也就是在二进制中不会超过31位数，那么之后我们可以遍历31位，逐位统计该位上异或和为1的子数组数量，最终累加所有位的贡献（其中涉及到位运算，这篇文章不做展开，但是这也是很重要的算法思想）。

#include <bits/stdc++.h>
using namespace std;

signed main()
{
	int n;
	cin >> n;
	long long ans = 0;
	vector<int> a(n + 1, 0);
	vector<vector<int>> cnt(31, vector<int>(2, 0));
	for(int i = 1; i <= n; ++ i) cin >> a[i], a[i] ^= a[i - 1];
	for(auto &x : cnt) x[0] = 1;//最开始异或前各位都为0
	
	for(int i = 1; i <= n; ++ i){
		for(int j = 0; j < 31; ++ j){
			int bit = (a[i] >> j) & 1;//判断此位是否为1
			ans += 1ll * cnt[j][!bit] * (1 << j);//累计贡献
			cnt[j][bit] ++;
		}
	}
	cout << ans << endl;
}