（基础算法）二维差分，前缀和

对于二维前缀和不再过多赘述，直接记根据容斥原理得到的公式或者对列先做前缀和，再对行进行前缀和得到都可以，这里为了和下面二维差分形成对比，简单写一下，由于比较直观，不再画图

for(int i = 1; i <= n; ++ i)
	{
		for(int j = 1; j <= m; ++ j)a[i][j] += a[i][j - 1];
		for(int j = 1; j <= m; ++ j) a[i][j] += a[i - 1][j];
	}

由于差分是前缀和的逆运算，在二维里不容易想象，记公式容易和二维前缀和公式搞混，所以用下面的图和代码表示一种不用死记公式的方式

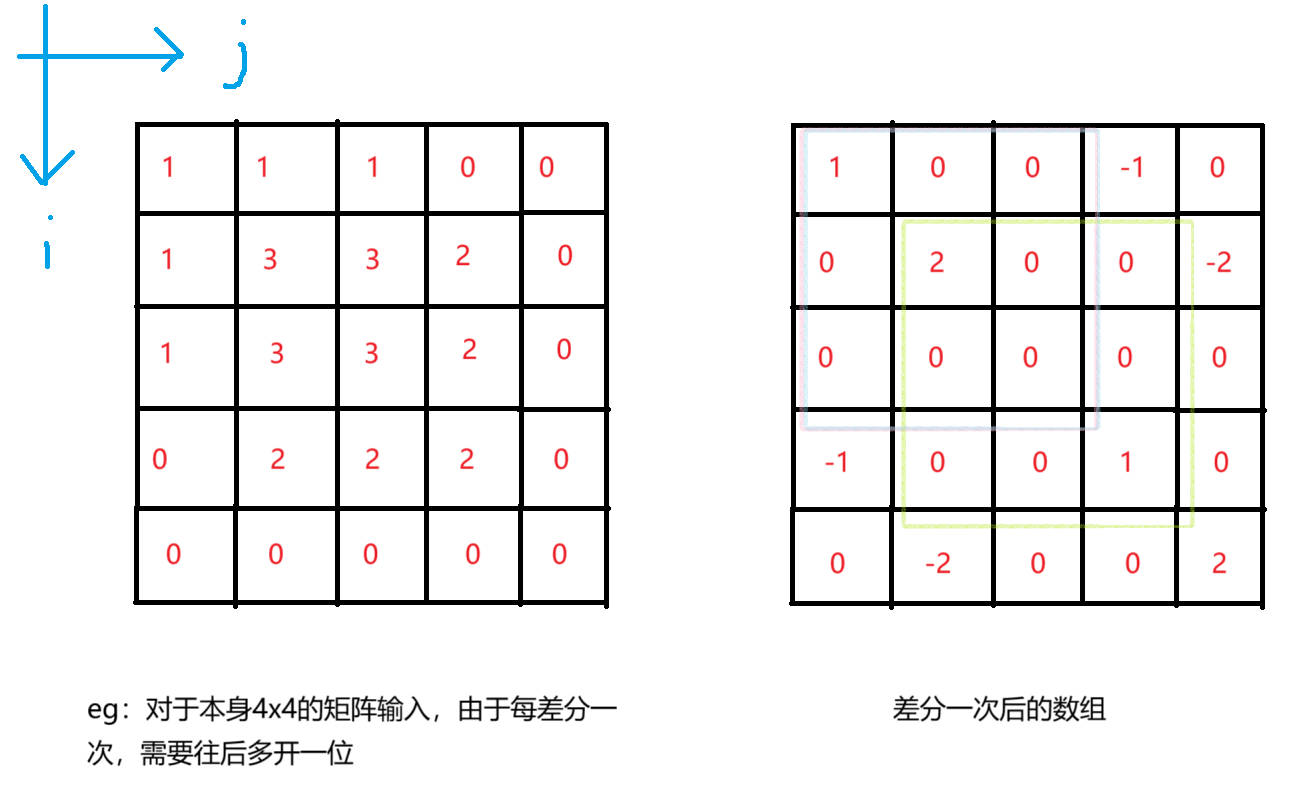
for(int i = n; i >= 0; -- i)
	{
		for(int j = n; j >= 0; -- j)
		{
			if(i) g[i][j] -= g[i - 1][j];//防止越界，行与行差分
		}
		for(int j = n; j >= 0; -- j)  if(j) g[i][j] -= g[i][j - 1];//列与列差分
	}

注意行与列差分的先后顺序，以免多减或者少减

思维扩展：用于贴邮票，铺地砖等类型的算法题