数据结构——树(Java语言描述)

一.树的基本元素

1.元素组成:

1. 树根:rootNode. 树只有一个树根。
2. 节点:Node. 树上的所有节点。
3. 子节点数组:Node[]. 数组代表每个节点的所有子节点
4. 父节点:parentNode. 每个节点只有一个父节点。

2. Node为Tree中的内部类

1. parent ：指向父节点的引用
2. childern: 孩子数组，存储该节点的所有子节点。
3. T 为泛型参数,代表节点应该存储什么类型的数据，是该节点的数据域。
4. size: 该节点所有的孩子数目。(孩子数组中所有元素的数目)

3.Tree类(Tree就是对树进行增删改查的实现类,该类内部维护了一个树根节点。)

1. treeRoot:Tree进行维护的一个树根节点。

2. cur:代表当前节点的引用,用于各种方法中,减少空间复杂度。

3. DEFAULT_SIZE:孩子节点数组的默认大小,数值为10.

4. findNodes():该方法返回当前节点的孩子节点数组。

5. find():该方法实现返回树中节点的引用功能,用于遍历树节点并且提供当前操作节点的功能。

6. add():该方法实现对节点的添加,内部调用了find()与addNode()方法实现父类节点的查找与节点数组的动态扩容。

3.实现思路:

代码1:建立一个Tree类。该类内部维护一个顺序树,对外提供基于树的增删改查的方法.该代码是整个树结构的组成单元。

@SuppressWarnings(value = "all")
public class Tree<T> {
	// 基于数组的树
	
	//孩子数组默认初始大小
	static int DEFAULT_SIZE = 10;
	
	//树根,Tree对象负责维护该对象。
	private Node treeRoot;

	//指向当前叶子的指针
	private Node cur;
	
	//节点内部类,树结构的基本组成单位。
	static class Node<T> {
	
		//孩子数组中元素的个数
		private int size = 0;
		
		//父节点指针
		private Node<T> paraent;

		private Node<T>[] children = new Node[DEFAULT_SIZE];
		
		//叶子数据域
		private T t;

		//叶子名称
		private String name;
		
		//Node对外提供两个构造方法.一个无参构造用于构造树根元素,另外一个负责构造叶子节点元素。
		public Node() {
			this.name = "树根";
		}

		public Node(T t, String name) {
			this.t = t;
			this.name = name;
		}
	}
		//Tree构造器,构造一个TreeRoot
		public Tree() {
			treeRoot = new Node();
		}
}

代码2：add方法的实现

//方法需要传入一个节点指针引用

public void add(Node<T> node){
//调用find()方法找到当前操作节点,然后通过addNode()方法添加到该节点的孩子数组中
		Node parent = find();
		addNode(parent, node);
}

代码3:find()方法的实现:方法实现树的查询操作。
(代码有点长,我写的时候也有点晕了,不过想象成你在操作文件夹理解起来也 许就会轻松很多~)

public Node<T> find(){
		//使当前节点成为树根节点
		Node cur = treeRoot;
		Scanner scanner = new Scanner(System.in);
		
		//标识用户操作的字符串
		String flag = null;
		
		//标识节点在数组中的下标变量
		int index = 0;

		//用于接收当前节点的孩子数组
		Node[] nodes = null;
		
		//需要在循环条件下对节点进行挑选操作
		while(true){		
			System.out.println("当前父节点:"+cur.name);
			System.out.println("当前节点添加或者是否继续遍历子节点?");//
			//(ps:按1遍历当前节点的孩子数组,按2在当前节点插入叶子节点。就相当在当前文件夹添加文件，还是进入子文件夹中)
			flag = scanner.nextLine();
			//如果选择1，则表示遍历当前节点的孩子数组。
			if(flag.equals("1")){
				//通过finjNodes()方法得到当前节点的孩子节点数组
				nodes = findNodes(cur);
				//如果数组中的元素个数为0,则结束本次操作。
				if(cur.size==0){
						System.out.println("无子节点,本次插入操作结束!");
						return null;
				}
				//如果不为零则输出所有不为null的孩子节点
				for (int i = 0; i < nodes.length; i++) {
					if(nodes[i]!=null)
						System.out.print(nodes[i].name+"("+i+")"+" 		");
				}
				//选择一个节点进行操作
				System.out.println("请选中一个节点(ps:选择方式根据括号下标)");
				//操作使用while循环,防止用户输入字符不是数字而跳出try语句块。
				while(true){
					try {
						index = Integer.valueOf(scanner.nextLine());
						cur = nodes[index];
						if(cur==null){
							System.out.println("节点不存在,请重新输入");
							continue;
						}
						break;
					} catch (Exception e) {
						System.out.println("输入下标格式不正确,请重新输入!");
					}
				}
			}
			//不为1,则返回当前节点。
			else{
				/**try {
					
				} finally {
					//System.out.println("关闭流");
					//scanner.close();这里关闭流了,然后下次调用该方法反而会引发异常??
				}
				*/
				System.out.println();
				return cur;
			}
		}
	}

代码4:addNode()方法:

//该方法传入一个父节点与一个子节点指针
public void addNode(Node<T> parent, Node<T> node) {
		//如果父节点不为null	
		if(parent!=null){
			//得到父节点所有孩子的数量
			int size = parent.size;
			//在增加元素之前调用enSureSize()方法,进行是否需要扩容检查.
			enSureSize(size+1, parent);
			//父节点增加一个元素
			parent.children[size] = node;
			parent.size++;
		}
}

代码5: enSureSize()方法。检查是否需要调用gorw()方法实现动态扩容

public void enSureSize(int minCapcity, Node parent) {
		//minCapcity为父节点当前所有孩子的数量,从默认大小和孩子数量之间选择一个较大数
		minCapcity = Math.max(DEFAULT_SIZE, minCapcity);
		//如果孩子数量超过了当前数组的长度,则调用grow()方法
		if (minCapcity - parent.children.length > 0)
			grow(minCapcity, parent);
	}

代码6:grow()方法.。实现0.5倍的数组容量增长,或者整个数组的拷贝。

public void grow(int minCapcity, Node<T> parent) {
		//限制数组的最大长度
		if (minCapcity > Integer.MAX_VALUE - 8) {
			System.out.print("数组长度超过最大长度限制");
			return;
		}
		Node[] arrys = parent.children;
		int oldLength = arrys.length, newLength;
		newLength = oldLength + (int) (0.5 * oldLength);// 0.5倍扩容
		//如果数量大于新的数组长度,则让孩子数量为新的数组长度
		if (minCapcity > newLength)
			newLength = minCapcity;
		//Arrays工具类提供的一个native方法,实现数组的高效拷贝。
		parent.children = Arrays.copyOf(arrys, newLength);
	}

代码7:主函数用for循环实现一个节点数为10的树

public static void main(String[] args) {
		//实例化一个类型为String的Tree	
		Tree<String> tree = new Tree<String>();
		for (int i = 0; i < 10; i++) {
			//生成十个数据域为(0-10)随机数，名称为"Node"+i的叶子
			tree.add(new Node(""+(int)(Math.random()*10), "Node"+i));
		}
	}

4.实验效果图: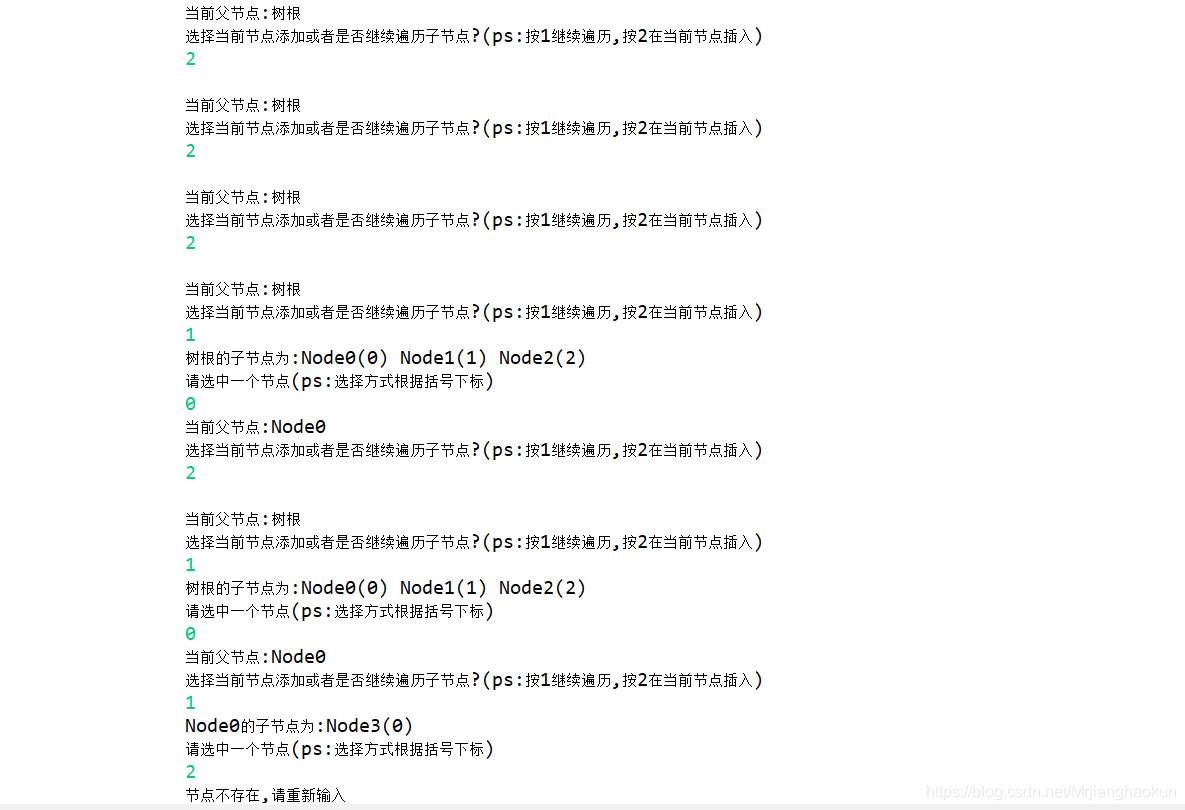

![Alt]
()

5.说明:

因为时间和个人能力有限,这次对于树的操作算法繁琐且有缺陷,因为每次查询就不能再返回父节点的位置,有兴趣的童鞋可以修改下代码~~~~~

6.总结:

此篇文章是以自己的角度来想象树应该是有怎么样的一个结构,通过怎么样的方法可以对它进行一系列的操作.其实通过文件系统我们可以更加理解树的构造和基本操作，例如windows下磁盘驱动器就好比如树的根节点,其子文件就相当于树的一片片叶子。在驱动器的基础上我们可以建立许多的文件夹,文件夹又可以放入许多的文件夹…虽然只提供了查询和增加节点的操作,但是相信伙伴们能在find()方法的基础上对节点实现删除和更新操作.(后续继续二叉树和平衡二叉树的总结)

第一次写文章有很多不足的地方，可能很多汉字没打对,或者代码整洁度和代码性能都非常一般但是也算是自己的一次进步了~还是那句话!完成该完成的事情！