递归实现指数型枚举

最新推荐文章于 2024-04-06 23:03:43 发布

原创最新推荐文章于 2024-04-06 23:03:43 发布 · 173 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++

准备蓝桥杯专栏收录该内容

35 篇文章

订阅专栏

本文介绍了一种使用递归搜索解决从1到n整数中选取任意多个数的所有可能组合的方法。通过构建递归搜索树，文章详细解释了如何通过选择和不选择每个数的策略来遍历所有可能性，最终实现输出所有方案的目标。

题目： 从 1~n 这 n 个整数中随机选取任意多个，输出所有可能的选择方案。

输入格式
输入一个整数n。

输出格式
每行输出一种方案。
同一行内的数必须升序排列，相邻两个数用恰好1个空格隔开。
对于没有选任何数的方案，输出空行。
本题有自定义校验器（SPJ），各行（不同方案）之间的顺序任意。

输入样例：

输出样例：

//空行（不会打出来，写字代替一下）
3
2
2 3
1
1 3
1 2
1 2 3

要想一个办法来搜索全部的结果，画出一个递归的搜索树来辅助写代码
下面来说明一下这个图的意思，用n=3来举例，三个位置则分别代表1,2,3这三个数，到最后有几就输出几
每一个位置我们都有两种选择，就是选择用这个数和不选用这个数即两个分支，直到三个位置都确定了之后开始进行输出（边界判断）

搜索树

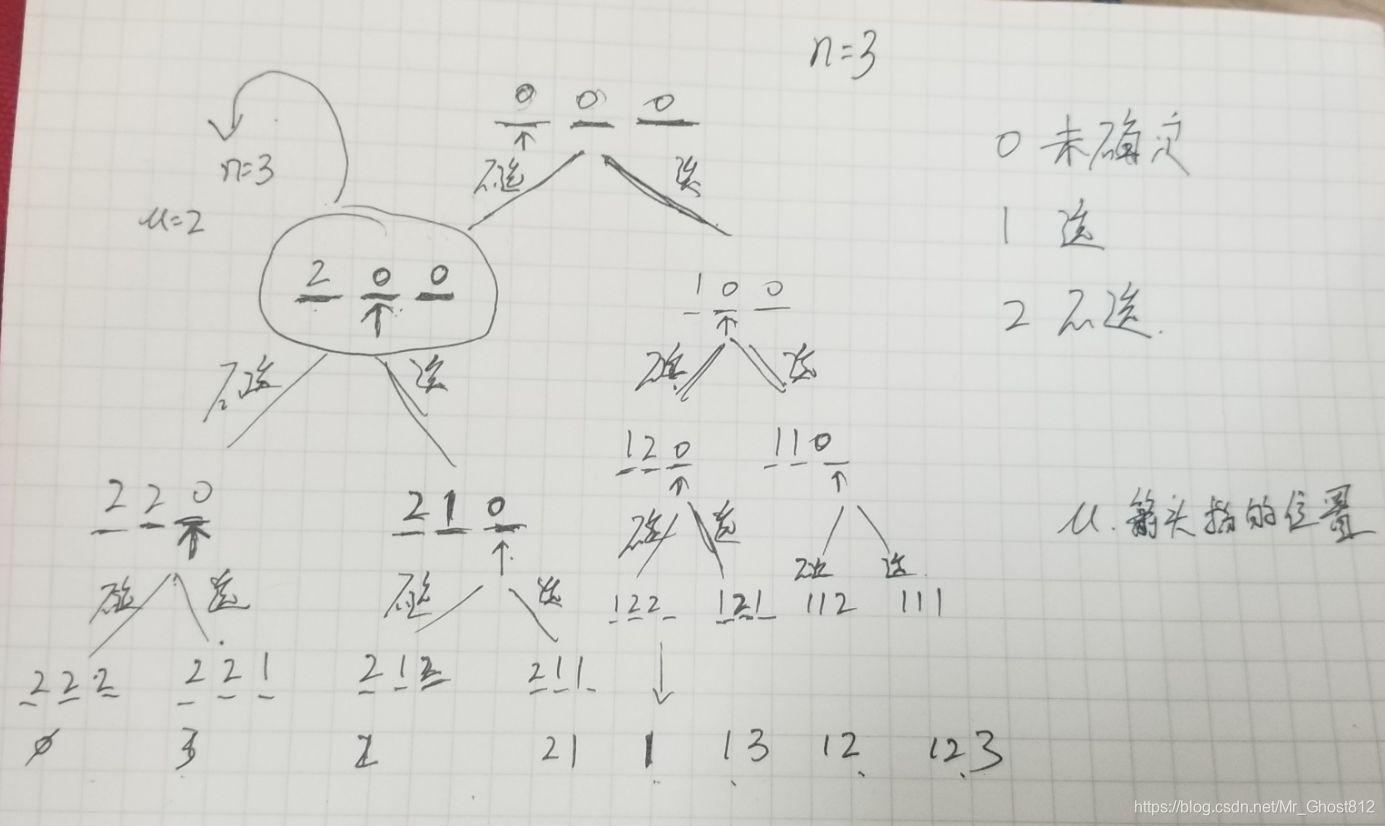
代码如下

#include<iostream>
#include<cstdio>
#include<string>
#include<algorithm>

using namespace std;

const int N = 16;

int n;
int st[N];

void dfs(int u)
{
    if(u == n)  //判断是否到了最后一个，u代表下标，用3举例，如果下标等于三了，则表示到了第四个位置，那么就到了该判断输出的时候了
    {
        for(int i = 0 ; i < n ; i++)
            if(st[i] == 1)
                printf("%d ", i+1);
        puts("");
        return;
    }
    
    st[u] = 2;   //2代表不选择这个数，即走不选的分支
    dfs(u + 1);  //走不选的分支，走一遍dfs
                    //走完之后走另一个分支的时候应该恢复现场，但是下面的操作会直接覆盖，省略掉
    
    st[u] = 1;    //1代表选择这个数，即走选择的分支
    dfs(u + 1);    //走选择的分支
    st[u] = 0;    //恢复现场
}

int main()
{
    cin >> n;
    dfs(0);    //0代表开始选择的位置，即图中箭头指向的位置，这里遵循数组的下标开始，并没从1开始
    return 0;
}