HNU人工智能导论作业2

人工智能导论清览第2次作业

1.请用真值表的方法证明下列语句是有效的，可满足的，还是不可满足的？

2.考虑下列的一阶逻辑表达式：

其中x,y,z,w,s,t是变量，a,b,c是常数。

a)讲1,2,3式子转换为CNF形式

b)从上述知识库(KB)中使用归结算法证明结论equal(c,a)

Answer：

3.把下列表达式转换为CNF形式

Answer：

4.考虑从一副标准的52张纸牌（不含大小王）中分发每手5张牌的扑克牌域。假设发牌人是公平的。

a)在联合概率分布中共有多少个原子事件（即，共有多少种5张手牌的组合）？(5分)

b)每个原子事件的概率是多少？(5分)

c)拿到大同花顺（即同花的A、K、Q、J、10）的概率是多少？(5分)

d)四同张（4张相同的牌，分别为4种花色）的概率是多少？(5分)

Answer：

5.贝叶斯网络

参考下图中的贝叶斯网络，其中布尔变量I=聪明(intelligence) ，H=诚实(Honest)， P=受欢迎的(Popular) ，L=大量的竞选资金 ，E=竞选成功

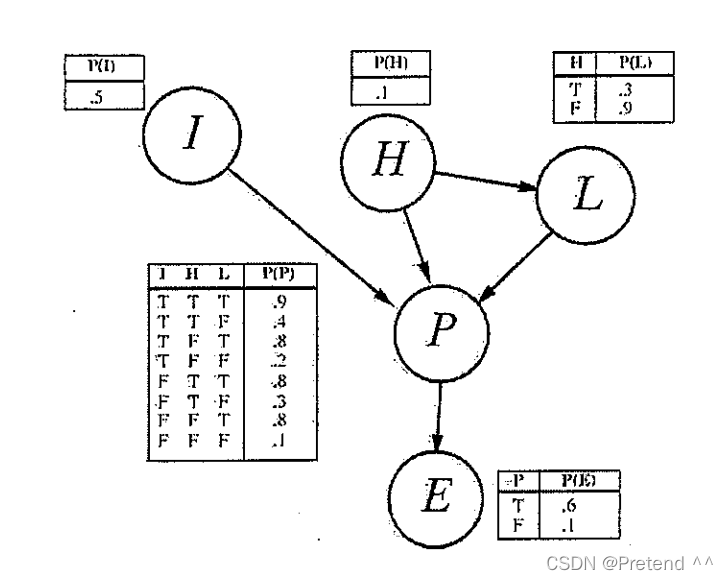
(a) 根据该网络结构，是否可以得到P(I,L,H)=P(I)P(L)P(H),如果不是，请给出正确的表达式；

(b)根据该网络结构计算P(i,h,¬l,p,¬e)的值，只有答案没有步骤不得分

(c )假设已知某个人是诚实的，没有大量的竞选资金但是竞选成功了，那么他是聪明的概率是多少？只有答案没有过程不得分。

Answer：