hdoj 1007 Quoit Design【分治法+平面最近点对】

最新推荐文章于 2023-04-15 17:15:52 发布

原创最新推荐文章于 2023-04-15 17:15:52 发布 · 329 阅读

0 ·

CC 4.0 BY-SA版权

基础题目专栏收录该内容

22 篇文章

订阅专栏

该博客讨论了如何利用分治法解决一个在Cyberground游戏中找到最大半径环以包围所有玩具的问题。内容涉及到平面最近点对的计算，指出当两个玩具坐标相同时，环的半径为0。博客提供了一个样例输入和输出，并提到在合并分治结果时的特殊情况，即左半部分的一个点与右半部分的点之间的距离小于当前最小距离时，右半部分可能最多只有6个点。尽管存在证明，但博主没有在代码中使用这一特性，而是参照了其他解决方案。

Problem Description

Have you ever played quoit in a playground? Quoit is a game in which flat rings are pitched at some toys, with all the toys encircled awarded.
In the field of Cyberground, the position of each toy is fixed, and the ring is carefully designed so it can only encircle one toy at a time. On the other hand, to make the game look more attractive, the ring is designed to have the largest radius. Given a configuration of the field, you are supposed to find the radius of such a ring.

Assume that all the toys are points on a plane. A point is encircled by the ring if the distance between the point and the center of the ring is strictly less than the radius of the ring. If two toys are placed at the same point, the radius of the ring is considered to be 0.

Input

The input consists of several test cases. For each case, the first line contains an integer N (2 <= N <= 100,000), the total number of toys in the field. Then N lines follow, each contains a pair of (x, y) which are the coordinates of a toy. The input is terminated by N = 0.

Output

For each test case, print in one line the radius of the ring required by the Cyberground manager, accurate up to 2 decimal places.

Sample Input

0 0

1 1

-1.5 0

0 0

0 1.5

Sample Output

0.71

0.00

0.75

题意：求平面上最近点对。

题解：我们可以采用分治法，核心就是在合并的时候需要注意一下。

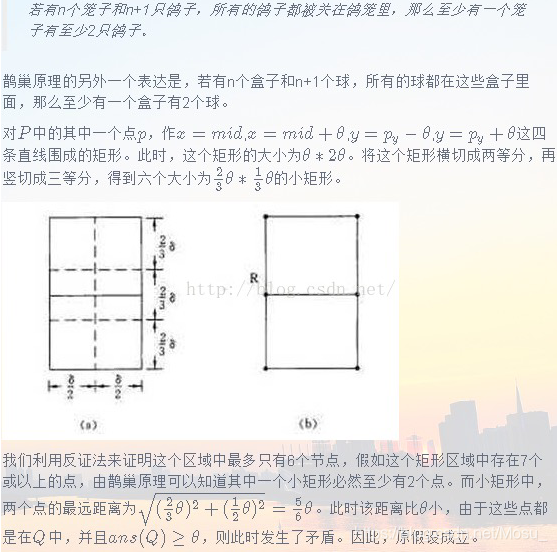
参考网上的一些题解，关于分治之后，左半面一个点和右半面的点距离小于最小距离，在右半面只可能存在最多六个点。由于代码直接过掉了，就没有用这个去写，只是看了相关证明。

关于证明采用鸽巢原理的思想。

#include<bits/stdc++.h>
using namespace std;

const int MAXN = 0x7f7f7f7f;
struct Node{
    double x, y;
}s[100009];
int t[100009];

bool cmp1(Node a, Node b){
    if(a.x == b.x)
        return a.y < b.y;
    return a.x < b.x;
}
bool cmp2(int a, int b){
    return s[a].y < s[b].y;
}
double dict(Node a, Node b){
    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
double solution(int l, int r){
    if(l == r)
        return MAXN;
    if(l + 1 == r)
        return dict(s[l], s[r]);
    int mid = (l + r) >> 1;
    double lmin = solution(l, mid);
    double rmin = solution(mid + 1, r);
    double Min = min(lmin, rmin);
    int k = 0;
    for(int i = l; i <= r; i++)
        if(fabs(s[i].x - s[mid].x) < Min)
            t[k++] = i;
    sort(t, t + k, cmp2);
    for(int i = 0; i < k - 1; i++)
        for(int j = i + 1; j < k && fabs(s[t[i]].y - s[t[j]].y) < Min; j++){
            double newd = dict(s[t[i]], s[t[j]]);
            if(newd < Min)
                Min = newd;
        }
    return Min;
}
int main(){
    int n;
    while(scanf("%d", &n) != EOF){
        if(n == 0)
            break;
        for(int i = 0; i < n; i++){
            scanf("%lf%lf", &s[i].x, &s[i].y);
            //cin >> s[i].x >> s[i].y;
        }
        sort(s, s + n, cmp1);
        printf("%.2lf\n", solution(0, n - 1) / 2);
    }
    return 0;
}