二叉树的相关操作

最新推荐文章于 2022-07-06 16:49:23 发布
原创 最新推荐文章于 2022-07-06 16:49:23 发布 · 235 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

1.定义二叉树的结构体

#pragma once 

#include 

typedef char TreeNodeType; 

typedef struct TreeNode { 
 TreeNodeType data; 
 struct TreeNode* lchild; //左孩子指针
 struct TreeNode* rchild; //右孩子指针
} TreeNode;

2.初始化二叉树

void TreeInit(TreeNode** root){
    if(root==NULL){
        return;
    }   
    *root=NULL;
}

3.创建二叉树的节点

开辟动态内存空间来保存节点信息。

TreeNode* CreateTreeNode(TreeNodeType value){
    TreeNode* new_node=(TreeNode*)malloc(sizeof(TreeNode));
    new_node->data=value;
}

4.通过递归的方法来前序遍历访问二叉树

前序遍历：先访问根结点，再访问左子树，最后访问右子树

void PreOrder(TreeNode* root){
    if(root==NULL){
        printf("#");
        return;
    }
    printf("%c",root->data);
    PreOrder(root->lchild);
    PreOrder(root->rchild);
}

5，通过递归的方法来中序遍历访问二叉树

中序遍历：先访问左子树，再访问根结点，最后访问右子树

void InOrder(TreeNode* root){
    if(root==NULL){
        return; 
    }
    InOrder(root->lchild);
    printf("%c ",root->data);
    InOrder(root->rchild);
}

6，通过递归的方法来后续遍历二叉树

后序遍历：先访问左子树，再访问右子树，最后访问根节点

void PostOrder(TreeNode* root){
    if(root==NULL){
        return;
    }
    PostOrder(root->lchild);                                                    
    PostOrder(root->rchild);
    printf("%c ",root->data);

}

7.层序遍历二叉树

层序遍历思想：利用队列


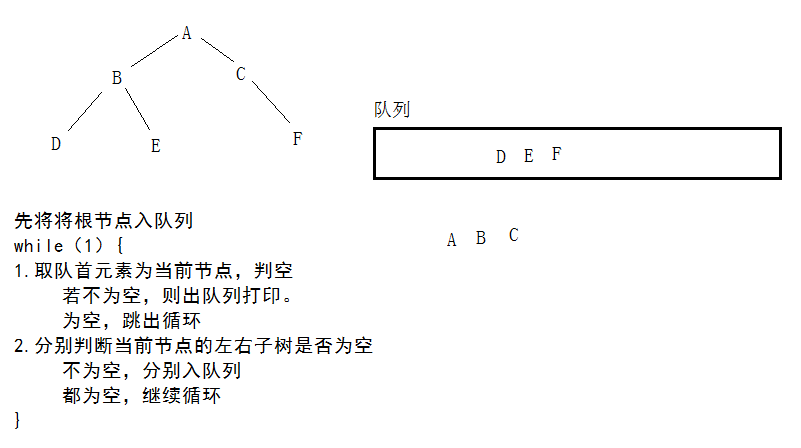
void LevelOrder(TreeNode* root){
    seqqueue q;
    seqqueuePush(&q,root);                                                      
    //2.循环的取队首元素
    TreeNode* cur=NULL;
    while(seqqueueTop(&q,&cur)){
    //3.访问队首元素并出队列
        printf("%c ",cur);
        seqqueuePop(&q);
        if(cur->lchild!=NULL){
            seqqueuePush(&q,cur->lchild);
        }
        if(cur->rchild!=NULL){
            seqqueuePush(&q,cur->rchild);
        }
    //4.将队首元素的左子树节点和右子树节点都依次入队列
    //5.进入下一次循环，直到队列为空，说明遍历完了
    }
}

8.通过给定的前序遍历的字符串数组来创建二叉树

前提：前序遍历的节点里若左右子树不存在则用‘#’代替

TreeNode* _TreeCreate(TreeNodeType array[],size_t size,size_t* index,TreeNodeType null_node){
    if(index==NULL){
        return NULL;
    }                                                                                
    if(*index>=size){
        return NULL;
    }
    if(array[*index]==null_node){
        return NULL;
    }
    TreeNode* new_node=CreateTreeNode(array[*index]);
    ++(*index);
    new_node->lchild=_TreeCreate(array,size,index,null_node);
    ++(*index);
    new_node->rchild=_TreeCreate(array,size,index,null_node);
    return new_node;
}
TreeNode* TreeCreate(TreeNodeType array[],size_t size,TreeNodeType null_node){
      size_t index=0;
      return _TreeCreate(array,size,&index,null_node);
    
}

测试代码

void TestCreateTree(){
    TestHeader;
    TreeNode* root;
    TreeNodeType array[]="abd##e##c#f##";//前序遍历的结果
    root=TreeCreate(array,strlen(array),'#');
    printf("前序遍历为：");
    PreOrder(root);
    printf("\n");
    printf("中序遍历为：");
    InOrder(root);
    printf("\n");

    printf("后序遍历为：");
    PostOrder(root);                                                                 
    printf("\n");

}

9.销毁二叉树

void TreeDestroy(TreeNode** root){
    if(root==NULL){
        return ;
    }
    if(*root==NULL){
        return;
    }
    TreeNode* to_delete=*root;
    TreeDestroy(&to_delete->lchild);
    TreeDestroy(&to_delete->rchild);                                                 
    Destroy(to_delete);
}

10.克隆二叉树

TreeNode* TreeClone(TreeNode* root){                                                 
    if(root==NULL){
        return NULL;
    }
    TreeNode* new_node=CreateTreeNode(root->data);//创建新的二叉树根结点
    new_node->lchild=TreeClone(root->lchild);
    new_node->rchild=TreeClone(root->rchild);
    return new_node;
}

11.求一棵树中节点的个数

思想：节点的个数=根结点+根结点所有的左子树节点个数+根结点所有的右子树节点个数

size_t TreeSize(TreeNode* root){
    if(root==NULL){
        return 0;
    }
    return 1+TreeSize(root->lchild)+TreeSize(root->rchild);
}

12.求第K层节点的个数

思想：向下递归，每递归一次K-1，当K=1时即为当前要找的K层

size_t TreeKLevelSize(TreeNode* root, int k){
    if(root==NULL||k<1){
        return 0;
    }
    if(k==1){
        return 1;
    }
    return TreeKLevelSize(root->lchild,k-1)+TreeKLevelSize(root->rchild,k-1);        
}

13.求二叉树的高度

size_t TreeHeight(TreeNode* root){
    if(root==NULL){
        return 0;
    }
   size_t m=TreeHeight(root->lchild) ;
   size_t n=TreeHeight(root->rchild);
   return 1+(m>n?m:n);
}

14.查找节点

TreeNode* TreeFind(TreeNode* root, TreeNodeType to_find){
    if(root==NULL){
        return NULL;
    }
    if(root->data==to_find){
        return root;
    }
    TreeFind(root->lchild,to_find);
    TreeFind(root->rchild,to_find);
}

15.查找所给节点的左子树，右子树，父节点

TreeNode* LChild(TreeNode* node){
    if(node==NULL){
        return NULL;
    }
    return node->lchild;
}                                                                                    
TreeNode* RChild(TreeNode* node){
    if(node==NULL){
        return NULL;
    }
    return node->rchild;
}

TreeNode* Parent(TreeNode* root, TreeNode* node){
    if(node==NULL||root==NULL){
        return NULL;
    }
    if(root->lchild==node||root->rchild==node){
        return root;
    }
    TreeNode* lret=Parent(root->lchild,node);
    TreeNode* rret=Parent(root->rchild,node);
    return lret!=NULL?lret:rret;
}

16.非递归前序遍历二叉树



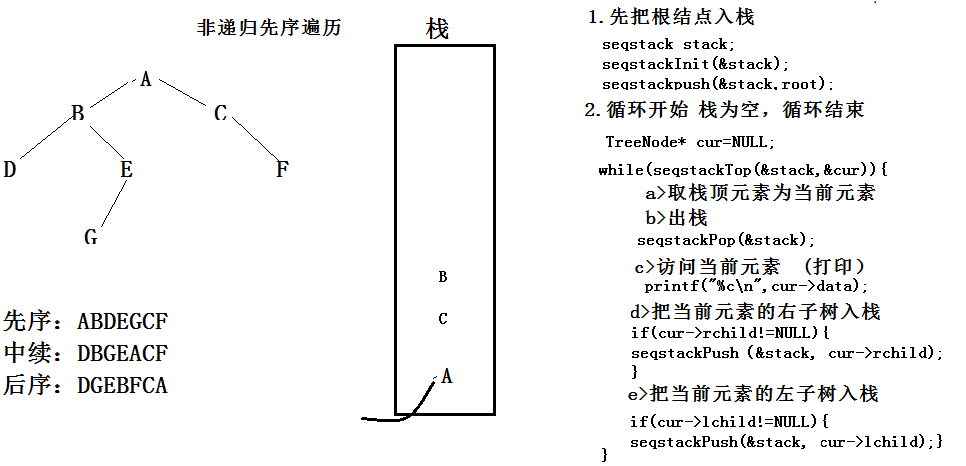
void PreOrderByLoop(TreeNode* root){
    if(root==NULL){
        return;
    }
   seqStack stack;
   seqStackInit(&stack);
   seqStackPush(&stack,root);
   TreeNode* cur=NULL;
   while(seqStackFront(&stack,&cur)){
        printf("%c ",cur);
        seqStackPop(&stack);
        if(cur->lchild!=NULL){
           seqStackPush(&stack,cur->lchild) ;
        }
        if(cur->rchild){                                                             
            seqStackPush(&stack,cur->rchild);
        }
   }
}

17.非递归中序遍历二叉树


void InOrderByLoop(TreeNode* root){
    if(root==NULL){
        return;
    }
    seqStack stack;
    seqStackInit(&stack);
    TreeNode* cur=root;
    while(1){
        while(cur!=NULL){
            cur=cur->lchild;
            seqStackPush(&stack,&cur);
        }
        TreeNode* top=NULL;
        int ret=seqStackFront(&stack,&top);
        if(ret==0){
            return;
        }
        seqStackPop(&stack);
        cur=top->rchild;                                                             
    }
    return;
}

18.非递归后序遍历二叉树


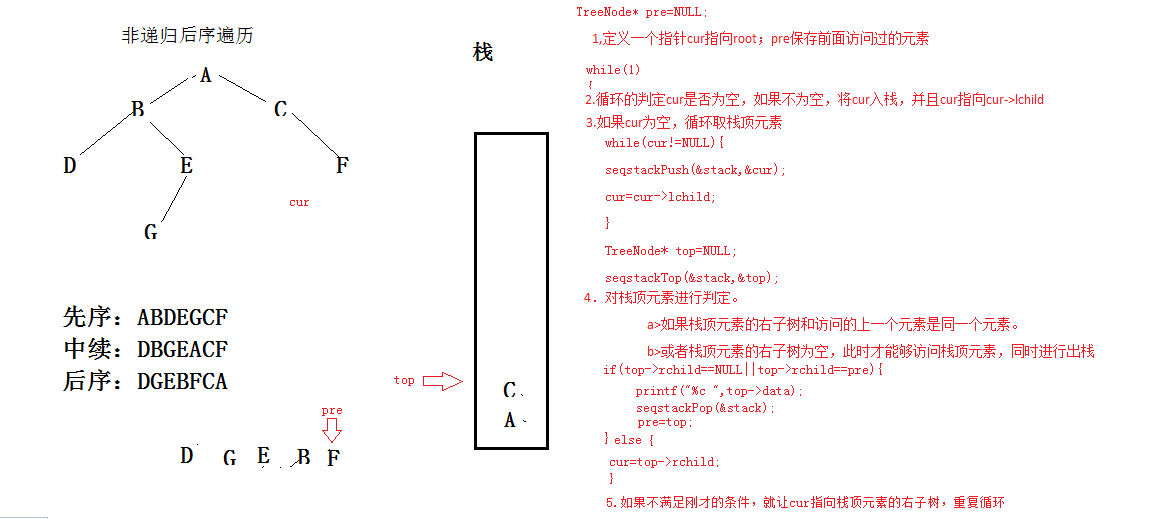
void PostOrderByLoop(TreeNode* root){
    if(root==NULL){
        return;
    }
    seqStack stack;
    seqStackInit(&stack);
    TreeNode* cur=root;//cur保存当前节点
    TreeNode* pre=NULL;//pre保存前一个访问过的节点
    while(cur!=NULL){
        seqStackPush(&stack,&cur);
        cur=cur->lchild;
    }
    TreeNode* top=NULL;
    seqStackFront(&stack,&top);
    if(top->rchild==NULL||top->rchild==pre){
        printf("%c ",top);
        seqStackPop(&stack);
        pre=top;                                                                     
    }else{
        cur=top->rchild;
    }
}

19.镜像二叉树


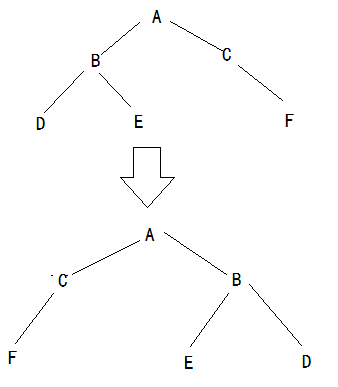
//递归版本
void swap(TreeNode** lnode,TreeNode** rnode){
    TreeNode* tmp=*lnode;
    *lnode=*rnode;
    *rnode=tmp;
    return;
}
void TreeMirror(TreeNode* root){
    if(root==NULL){
        return;
    }
    //访问动作就是交换左右子树
    swap(&root->lchild,&root->rchild);
    TreeMirror(root->lchild);
    TreeMirror(root->rchild);
}
//非递归版本
void TreeMirrorByLoop(TreeNode* root){
    if(root==NULL){
        return;
    }                                                                                
    seqqueue q;
    seqqueueInit(&q);
    seqqueuePush(&q,root);
    TreeNode* cur=NULL;
    while(seqqueueTop(&q,&cur)){
        swap(&cur->lchild,&cur->lchild);
        seqqueuePop(&q);
        if(cur->lchild!=NULL){
            seqqueuePush(&q,cur->lchild);
        }
        if(cur->rchild!=NULL){
            seqqueuePush(&q,cur->rchild);
        }
    }
    return;
}

20.判断二叉树是否为完全二叉树

思想：
阶段一：任何一个节点同时具备左右子树，一旦发现某个节点不是同时具备
a>当前节点只有右子树，一定不是完全二叉树
b>如果当前节点只有左子树，进入阶段二
c>如果当前节点没有子树，也进入阶段二


阶段二：任何一个节点都必须没有子树

当遍历结束之后，所有的条件都满足，说明这个树是二叉树，否则，不是。

int IsCompleteTree(TreeNode* root){
    if(root==NULL){
        return 0;
    }
    int if_start_step_two_flag=0;
    seqqueue q;
    seqqueueInit(&q);
    seqqueuePush(&q,root);
    TreeNode* cur=NULL;
    while(seqqueueFront(&q,&cur)){
        seqqueuePop(&q);
        if(if_start_step_two_flag==0){
            if(cur->lchild!=NULL&&cur->rchild!=NULL){
                seqqueuePush(&q,cur->lchild);
                seqqueuePush(&q,cur->rchild);
            }else if(cur->lchild==NULL&&cur->rchild!=NULL){
                return 0;
            }else if(cur->lchild!=NULL&&cur->rchild==NULL){
                if_start_step_two_flag=1;                                            
                seqqueuePush(&q,cur->lchild);
            }else{
                if_start_step_two_flag=1;
            }
        }else{
            if(cur->lchild==NULL&&cur->rchild==NULL) {
                ;
            }else{
                return 0;
            }
        }
    }
}

Moralin_
关注
编程题——二叉树后序遍历 python
Gillian_cc的博客
07-12 384
输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果，如果是返回true，否则返回false。假设输入的数组的任意两个数字互不相同。 二叉搜索树性质：左子树上的节点值<根节点值<右子树上的节点值，左右子树也为二叉搜索树 后序遍历性质：数组中最后一个元素为根节点，前面n-1个元素可分为左子树节点值、右子树节点值两部分 思路：确定数组最后一个元素为根节点，找出分界点，将前n-1个元素分为两部分，其中前半部分为左子树节点值，它们的值都比跟根节点值小；后半部分为右子树节点值，他们的值.
二叉树相关操作
01-04
二叉树基本操作：定义、建立、输入、输出等操作以及各种遍历，交换using namespace std; //二叉树定义 typedef char ElementType; typedef struct BiTreeNode { ElementType data; struct BiTreeNode* lchild; ...
数据结构之二叉树
weixin_30776273的博客
02-26 137
二叉树是一种简单的树形结构，其每个节点的分支节点数有0,1或2个。如下图T1,T2和T3是三棵二叉树。显然二叉树是一种递归的结构。 不包含任何节点的二叉树为空树，只有一个节点的二叉树称为单点树，一个节点的子节点的个数称为该节点的度。如果每个分支节点的度都为2，则称之为满二叉树。T4,T5就是两棵满二叉树。 如果一棵二叉树，除最后一层外，其它层的节点都是满的，而最后一层节...
二叉树(2.二叉树的遍历和实现)
水澹澹兮生烟
06-06 875
##2.5二叉树的遍历 什么是遍历?按照某种特性规则，对二叉树中的结点进行某种相应的操作，并且每个结点只操作一次。 ###2.5.1前序遍历 又称先根遍历，访问根结点的操作发生在遍历其左右子树之前。 //前序遍历 void preorder(node* root){ if(root){ printf("%d" ,root->data); preorder(root->left); preorder(root->right); } } ###2.5.2中序遍历 又称中根遍
二叉树的基本操作及面试题
xiaoxiaoyu
08-03 310
typedef int DataType; typedef struct BinaryTreeNode { struct BinaryTreeNode* _left; struct BinaryTreeNode* _right; BTDataType _data; }BTNode; BTNode* BuyBTNode(BTDataType x)//创建新结点 ...
二叉树：root==NULL和*root==NULL的区别
行步至春深
08-08 768
root == NULL 通常为查找的递归边界，说明当前结点不存在。 *root == NULL 表明当且结点存在，但是内容不存在。是创建一棵二叉树时的初始化操作。 前者常用得多。
二叉树相关操作---纯代码实现详解
热门推荐
weixin_64067830的博客
07-06 6万+
二叉树相关操作---纯代码实现详解，快来看看吧！
二叉树相关操作的实现
m0_52387040的博客
05-10 515
实 验 报 告 实验名称 二叉树相关操作的实现 一、实验目的和要求 1.理解二叉树二叉链表的存储结构。 2.以二叉树二叉链表的存储结构，实现二叉树的基本操作。 3.掌握二叉树二叉链表存储结构下，相关递归算法的实现。 二、实验内容: （一）完成二叉树二叉链表结构的定义 （二）实现二叉链表创建二叉树，并实现先序、中序和后序遍历算法。 （三）实现二叉树求结点个数，求树的高度，求叶子结点数、交换二叉树左右子树的算法。 三、实验环境(实验设备) Visual Studio等 Visual Studio 2019 实
数据结构实验——二叉树相关操作
05-13
本人本科期间数据结构二叉树的实验 1、建立二叉树的存储结构 2、先序、中序、后序遍历二叉树（要求任选某一种用非递归算法完成） 3、查询二叉树中某个结点 4、统计二叉树中叶子结点的个数 5、求二叉树的深度 6、要求...
二叉树相关操作java实现
04-22
1:构造一个二叉树 2:二叉树前序遍历(递归) 3:二叉树中序遍历(递归) 4:二叉树后续遍历(递归) 5:二叉树前序遍历(非递归) 6:二叉树中序遍历(非递归) 7:二叉树后序遍历(非递归)
二叉树相关操作代码
05-08
根据给定文件的信息，我们可以详细地探讨一下二叉树数据结构以及如何通过...以上就是对给定文件中所涉及的二叉树相关操作的详细解析。通过对这些操作的理解和实现，可以帮助我们更好地掌握二叉树这一重要的数据结构。
数据结构——二叉树有关操作程序
12-17
二)二叉树的一些基本操作 (1)返回二叉树的根； (2)返回树中某个结点的左孩子，若无则返回“空”； (3)返回树中某个结点的双亲，如果是根结点，则返回“空”； 三) 在（二）的基础上，求二叉树的深度+结点数 (1)求...
supervisor-4.2.2-1.el8.tar.gz
最新发布
08-16
# 适用操作系统：Centos8 #Step1、解压 tar -zxvf xxx.el8.tar.gz #Step2、进入解压后的目录，执行安装 sudo rpm -ivh *.rpm
运用强化学习技术实现自动驾驶智能车在简化世界有限时间内高效抵达目的地
08-16
资源下载链接为： https://pan.quark.cn/s/1aee9b26d465 运用强化学习技术实现自动驾驶智能车在简化世界有限时间内高效抵达目的地（最新、最全版本！打开链接下载即可用！）
stc8时间片轮询模板
08-16
stc8工程,stc8时间片轮询模板
【增强现实技术】基于ARKit和SceneKit的iOS AR应用开发：实现平面检测与3D物体交互功能
08-16
内容概要：本文档提供了一个基于iOS平台的增强现实（AR）应用程序示例，该应用利用了ARKit和SceneKit框架。程序的主要功能是在检测到的水平平面上放置3D物体（如球体），并且可以通过点击屏幕来触发物体的放置。程序中详细展示了如何配置AR会话、处理平面检测、响应用户交互以及管理AR会话的状态变化（如会话失败、中断等）。此外，还介绍了自定义平面节点的创建方法，包括设置平面的可视化效果和物理属性，确保放置的物体能够在平面上正确显示和互动。; 适合人群：对iOS开发有一定了解，尤其是对ARKit和SceneKit有初步认识的开发者。; 使用场景及目标：①学习如何在iOS平台上使用ARKit和SceneKit创建基本的AR应用；②掌握平面检测、物体放置、用户交互处理等核心功能的实现；③理解AR会话的管理和状态变化处理机制。; 其他说明：此示例代码为初学者提供了完整的项目结构和功能实现，建议开发者在实际开发中根据需求进行扩展和优化。同时，注意结合官方文档深入理解各个API的具体用法。
JAVA语言考试系统的设计与实现(论文+源代码+文献综述+外文翻译+开题报告)
08-16
java
机动车驾驶员网络学习平台自动刷在线学时
08-16
资源下载链接为： https://pan.quark.cn/s/0bf65096976f 机动车驾驶员网络学习平台自动刷在线学时（最新、最全版本！打开链接下载即可用！）
二叉树操作与算法实现详解
下面详细讲解标题中提到的二叉树基本操作及其相关知识点。 一、二叉树结点的结构 在数据结构中，二叉树的每个节点由数据域和两个指向其左右子树的指针域组成。数据域可以是整数、字符或其他数据类型，左右指针域则...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值