Task03：栈与递归

最新推荐文章于 2025-07-22 09:45:43 发布

原创最新推荐文章于 2025-07-22 09:45:43 发布 · 392 阅读

3 ·

CC 4.0 BY-SA版权

本文介绍了栈的基本概念，包括定义、操作和Python实现。接着详细阐述了递归的概念，以汉诺塔问题为例，展示了递归的使用。最后，提出了车辆重排序问题，探讨如何通过类似汉诺塔的策略来解决火车车厢的重新排列问题。

1. 栈的定义与操作

1.1 栈的定义

插入（入栈）和删除（出栈）操作只能在一端（栈顶）进行的线性表。即先进后出（First In Last Out）的线性表。
顺序表模拟入栈、出栈单链表模拟入栈、出栈

1.2 栈的操作

入栈操作：将数据元素值插入栈顶。
出栈操作：移除栈顶的数据元素。
是否为空：判断栈中是否包含数据元素。
得到栈深：获取栈中实际包含数据元素的个数。
清空操作：移除栈中的所有数据元素。
获取栈顶元素。

1.3 栈的实现（python）

class Stack:
  """模拟栈"""
  def __init__(self):
    self.items = []
     
  def isEmpty(self):
    return len(self.items)==0
   
  def push(self, item):
    self.items.append(item)
   
  def pop(self):
    return self.items.pop()
   
  def peek(self):
    if not self.isEmpty():
      return self.items[len(self.items)-1]
     
  def size(self):
    return len(self.items)
s=Stack()
print(s.isEmpty())
s.push(4)
s.push('dog')
print(s.peek())
s.push(True)
print(s.size())
print(s.isEmpty())
s.push(8.4)
print(s.pop())
print(s.pop())
print(s.size())

2. 递归

如果一个函数在内部调用自身本身，这个函数就是递归函数。

汉诺塔问题

我们可以先假设除 a 柱最下面的盘子之外，已经成功地将 a 柱上面的 63个盘子移到了 b 柱，这时我们只要再将最下面的盘子由 a 柱移动到 c 柱即可。

当我们将最大的盘子由 a 柱移到 c 柱后，b 柱上便是余下的 63 个盘子，a 柱为空。因此现在的目标就变成了将这 63 个盘子由 b 柱移到 c 柱。这个问题和原来的问题完全一样，只是由 a 柱换为了 b 柱，规模由 64 变为了 63。因此可以采用相同的方法，先将上面的 62 个盘子由 b 柱移到 a 柱，再将最下面的盘子移到 c 柱。

以此内推，再以 b 柱为缓冲，将 a 柱上面的 62 个圆盘最上面的 61 个圆盘移动到 b 柱，并将最后一块圆盘移到 c 柱。

我们已经发现规律，我们每次都是以 a 或 b 中一根柱子为缓冲，然后先将除了最下面的圆盘之外的其它圆盘移动到辅助柱子上，再将最底下的圆盘移到 c 柱子上，不断重复此过程。

这个反复移动圆盘的过程就是递归，例如我们每次想解决 n 个圆盘的移动问题，就要先解决（n-1）个盘子进行同样操作的问题。

于是可以编写一个函数，move(n, a, b, c)。可以这样理解：move(盘子数量, 起点, 缓冲, 终点)。
1. a 上只有一个盘子的情况，直接搬到 c，代码如下:

if n == 1:
    print(a, '-->', c)

2. a 上不止有一个盘子的情况:

首先，需要把 n-1 个盘子搬到 b 柱子缓冲。打印出的效果是：a --> b。

move(n - 1, a, c, b)

再把最大的盘子搬到 c 柱子，也是最大尺寸的一个。打印出：a–>c。

move(1, a, b, c)

最后，把剩下 b 柱的 n-1 个盘子搬到 c 上，此时缓冲变成了起点，起点变成了缓冲。

move(n - 1, b, a, c)

利用 Python 实现汉诺塔问题

i = 0


def move(n, a, b, c):
    global i
    if (n == 1):
        i += 1
        print('移动第 {0} 次 {1} --> {2}'.format(i, a, c))
        return
    move(n - 1, a, c, b)
    move(1, a, b, c)
    move(n - 1, b, a, c)


move(3, "a", "b", "c")  

# 移动第 1 次 a --> c
# 移动第 2 次 a --> b
# 移动第 3 次 c --> b
# 移动第 4 次 a --> c
# 移动第 5 次 b --> a
# 移动第 6 次 b --> c
# 移动第 7 次 a --> c

3.练习-车辆重排序

假设一列货运列车共有n节车厢，每节车厢将停放在不同的车站。假定n个车站的编号分别为1至n，货运列车按照第n站至第1站的次序经过这些车站。车厢的编号与它们的目的地相同。为了便于从列车上卸掉相应的车厢，必须重新排列车厢，使各车厢从前至后按编号1至n的次序排列。当所有的车厢都按照这种次序排列时，在每个车站只需卸掉最后一节车厢即可。

我们在一个转轨站里完成车厢的重排工作，在转轨站中有一个入轨、一个出轨和k个缓冲铁轨（位于入轨和出轨之间）。图（a）给出一个转轨站，其中有k个（k=3）缓冲铁轨H1，H2 和H3。开始时，n节车厢的货车从入轨处进入转轨站，转轨结束时各车厢从右到左按照编号1至n的次序离开转轨站（通过出轨处）。在图（a）中，n=9，车厢从后至前的初始次序为5，8，1，7，4，2，9，6，3。图（b）给出了按所要求的次序重新排列后的结果。

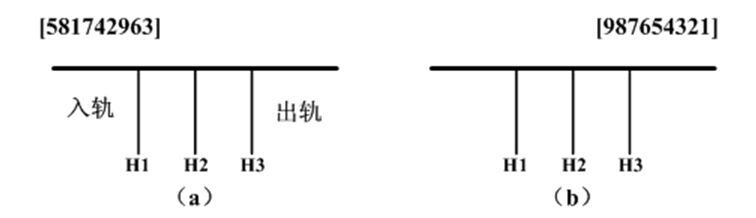
具有三个缓冲区铁轨的转轨站

编写算法实现火车车厢的重排，模拟具有n节车厢的火车“入轨”和“出轨”过程。

def output(stacks, n):
    global minVal, minStack
    stacks[minStack].pop()
    print('移动车厢 %d 从缓冲铁轨 %d 到出轨。' % (minVal, minStack))
    minVal = n + 2
    minStack = -1
    for index, stack in enumerate(stacks):
        if((not stack.isempty()) and (stack.top() < minVal)):
            minVal = stack.top()
            minStack = index

def inputStack(i, stacks, n):
    global minVal, minStack
    beskStack = -1  # 最小车厢索引值所在的缓冲铁轨编号
    bestTop = n + 1  # 缓冲铁轨中的最小车厢编号
    for index, stack in enumerate(stacks):
        if not stack.isempty():  # 若缓冲铁轨不为空
            # 若缓冲铁轨的栈顶元素大于要放入缓冲铁轨的元素，并且其栈顶元素小于当前缓冲铁轨中的最小编号
            a = stack.top()
            # print('stack.top()的类型是', a)
            if (a > i and bestTop > a):
                bestTop = stack.top()
                beskStack = index
        else:  # 若缓冲铁轨为空
            if beskStack == -1:
                beskStack = index
                break
    if beskStack == -1:
        return False
    stacks[beskStack].push(i)
    print('移动车厢 %d 从入轨到缓冲铁轨 %d。' % (i, beskStack))
    if i < minVal:
        minVal = i
        minStack = beskStack
    return True

def rail_road(list, k):
    global minVal, minStack
    stacks = []
    for i in range(k):
        stack = stack1.ArrayStack()
        stacks.append(stack)
    nowNeed = 1
    n = len(list)
    minVal = n + 1
    minStack = -1
    for i in list:
        if i == nowNeed:
            print('移动车厢 %d 从入轨到出轨。' % i)
            nowNeed += 1
            # print("minVal", minVal)
            while (minVal == nowNeed):
                output(stacks, n)  # 在缓冲栈中查找是否有需求值
                nowNeed += 1
        else:
            if(inputStack(i, stacks, n) == False):
                return False
    return True

if __name__ == "__main__":
    list = [3, 6, 9, 2, 4, 7, 1, 8, 5]
    k = 3
    minVal = len(list) + 1
    minStack = -1
    result = rail_road(list, k)
    while(result == False):
        print('需要更多的缓冲轨道，请输入需要添加的缓冲轨道数量。')
        k = k + int(input())
        result = rail_road(list, k)