数据结构——栈

保研C9！

已于 2024-12-03 16:40:49 修改

阅读量964

点赞数 37

分类专栏：数据结构文章标签：数据结构

于 2024-12-03 16:37:14 首次发布

本文链接：https://blog.youkuaiyun.com/MissedID_/article/details/144172584

版权

数据结构专栏收录该内容

9 篇文章

订阅专栏

一、栈

栈（stack）又称堆栈，是一种运算受限的线性表。栈的限制是仅允许在表的一端进行插入和删除操作，被允许操作的一端被称为栈顶，另一端则被称为栈底，如图下图所示。向一个栈中插入新元素又称入栈或压栈，它把新元素放到栈顶元素的上面，使之成为新的栈顶元素。从一个中删除元素又称出栈或退栈，它把栈顶元素删除，使其相邻的元素成为新的栈顶元素。由于堆栈只允许在一端进行操作，所以遵循后进先出（Last In First Out，LIFO）的操作原则。

栈的特点：后进先出

栈的操作：

        void init_stack(pStack stack); 初始化栈
        void push(pStack stack,int val); 入栈
        void pop(pStack stack); 出栈
        ElemType top(pStack stack); 返回栈顶元素（但不弹出）
        int isEmpty(pStack stack); 判断栈是否为空
        int stack_size(pStack stack); 栈的大小

注：“栈”这个名词，源自于英文单词“stack”，其字面意思是“堆叠”或“堆放”。由于这种像堆叠物品的方式或手枪弹夹装弹发射以及LIFO的特性，因而这个数据结构被称为“栈”。

（一）顺序栈

顺序栈，即栈的顺序存储结构是利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素，同时附设指针 top 指示栈顶元素在顺序栈中的位置。

1.1 第一种存储结构（从堆中获取连续空间）

一种通常的习惯做法是以 top=0 表示空栈，鉴于C语言中数组的下标约定从0开始，则当以C作描述语言时，如此设定会带来很大不便；另一方面，由于栈在使用过程中所需最大空间的大小很难估计，因此，一般来说，在初始化设空栈时不应限定栈的最大容量。一个较合理的做法是：先为栈分配一个基本容量，然后在应用过程中，当栈的空间不够使用时再逐段扩大。为此，可设定两个常量：STACK_INIT_SIZE（存储空间初始分配量）和 STACKINCREMENT （存储空间分配增量）。

存储结构：

  #define  STACK_INIT_SIZE  100; 
  #define  STACKINCREMENT   10;  
  typedef int SElemType;
  typedef struct 
  {
    SElemType  *base;  // 栈底指针
    SElemType  *top;   // 栈顶指针
    int  stacksize;    // 栈的当前可使用的最大容量
  } SqStack,*pSqStack;

base ：栈底指针，它始终指向栈底的位置，若 base 的值为 NULL,则表明栈结构不存在。

top：栈顶指针，其初值指向栈底，即 top= base 可作为栈空的标记。每当插入新的栈顶元素时，指针 top 增 1;删除栈顶元素时，指针 top 减 1。因此，非空栈中的栈顶指针始终在栈顶元素的下一个位置上。

栈的操作：

初始化栈：

void init_stack(pSqStack S)
{
    S->base=(SElemType*)malloc(STACK_INIT_SIZE*sizeof(SElemType));
    if(!S->base)
    {
        printf("存储空间分配失败");
        return;
    }
    S->top=S->base;
    S->stacksize=STACK_INIT_SIZE;
    printf("初始化成功");
    return;
}

入栈：

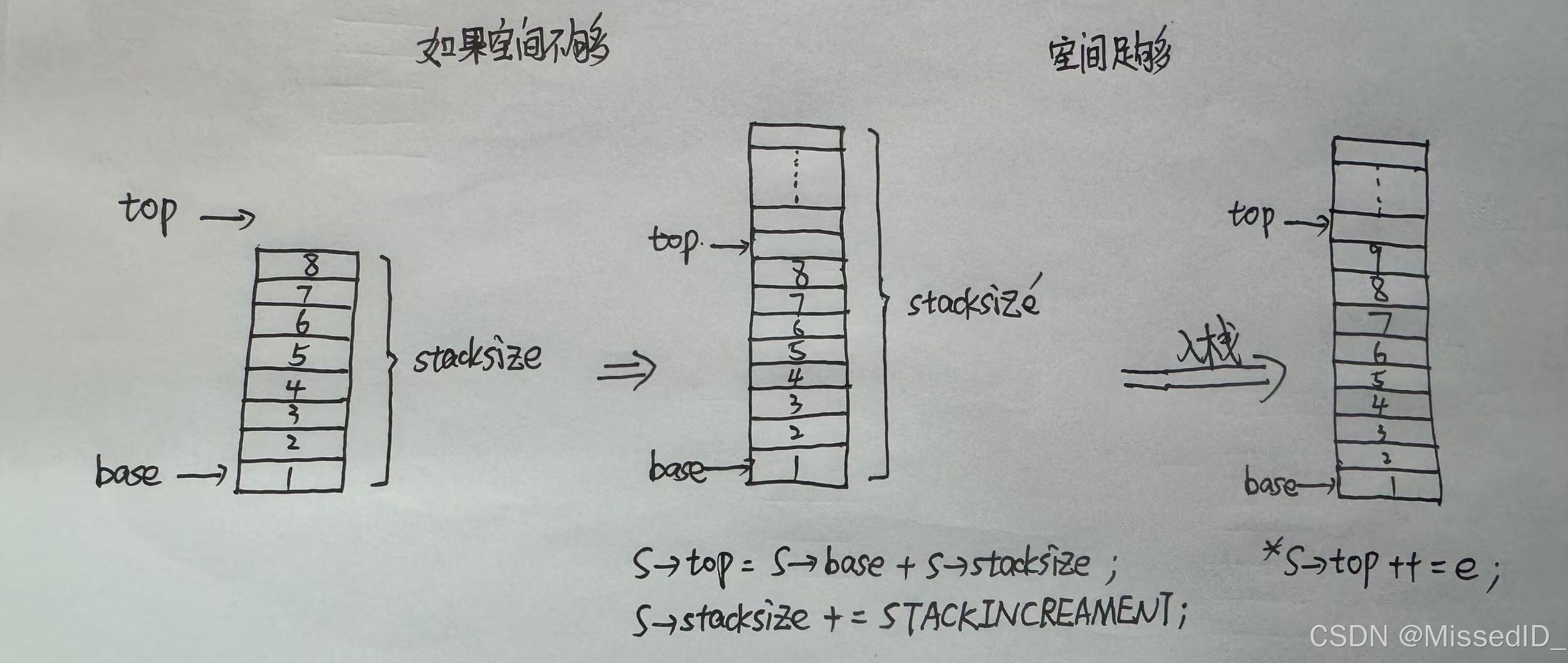
void push(pSqStaCk S,SElemType e)
{    
    if(S->top-S->base>=S->stacksize)
    {
        S->base=(SElemType)realloc(S->base,(S>stacksize+STACKINCREMENT)*sizeof(SElemType));
        if(!S->base)
        {
            printf("存储分配失败");
            return;
        }
        S->top=S->base+S->stacksize;
        S->stacksize+=STACKINCREAMENT;
    }
    *S->top++=e;
    return;
}

出栈：

SElemType pop(qSqStack S)
{    
    if(S->top=S->base)
    {
        printf("当前栈为空栈");
        return -1;
    }
    return *--S->top;
}

1.2 第二种存储结构（从栈中获取连续空间）

另一种常用的方法是采用数组实现栈，我们通过一个数组来存储栈的元素，并使用一个整型变量来指示栈顶元素的位置。这里给出一种典型的存储结构：

存储结构：

typedef int ElemType;
typedef struct Stack
{
    int data[STACK_SIZE]; // 用于存储栈元素的数组
    int top;            // 栈顶指针，指向当前栈顶元素的索引
                        // 对于空栈，top的值设置为-1
} Stack,*pStack;

栈的操作：

初始化栈:

void init_stack(pStack stack)
{
    stack->top=-1;
}

入栈:

void push(pStack stack, ElemType value)
{
    // 先判断栈是否已满，避免上溢
    if (isFull(stack))
    {
        printf("栈已满");
        return;
    }
    stack->data[++stack->top] = value;//前缀递增：先将变量++，再将变化后的变量放入整段表达式运算
                                      //后缀递增：先将整段表达式运算后再将变量++
    printf("已入栈:%d\n",value);
}

出栈:

ElemType pop(pStack stack)
{
    // 先检查栈是否为空，避免下溢
    if (isEmpty(stack))
    {
        printf("栈已空，不能弹出");
        return -1;
    }
    return stack->data[stack->top--];
}

返回栈顶元素:

ElemType top(pStack stack)
{
    // 先检查栈是否为空
    if (isEmpty(stack))
    {
        printf("栈为空");
        return -1;
    }
    return stack->data[stack->top];
}

判断栈是否为空:

int isEmpty(pStack stack)
{
    return (stack->top==-1)?1:0;
}

判断栈是否已满：

int isFull(pStack stack)
{
    return(stack->top == STACK_SIZE - 1) ? 1 : 0;
}

栈的大小:

int stack_size(pStack stack) 
{
    if (stack == NULL) 
    {
        return -1; // 返回 -1 表示栈指针无效
    }
    return stack->top + 1; // 栈中的元素个数是 top + 1
}

清空栈：

void clear(pStack stack)
{
    stack->top=-1;
}

输出栈的内容：

void printStack(pStack stack)
{
    if (isEmpty(stack))
    {
        printf("当前是个空栈！\n");
        return;
    }
    printf("当前栈中的内容如下：\n");
    for (int i = stack->top; i > -1; i--)
    {
        printf("[%d]:%d\n", i, stack->data[i]);
    }
    printf("========END========");
}

（二）链栈

这里用链表来实现栈。前面介绍了链表的增删查改，这里采用链表的头部插入法（头插法）、头部删除法来实现先进后出的效果。数据结构包括逻辑结构、存储结构和对数据的运算。栈的逻辑结构前面已经介绍，由于采用链表实现，所以具体的存储结构如下例所示。

存储结构：

typedef int ElemType;
// 定义栈的结点
typedef struct Node
{
    ElemType data;
    struct Node *next;
}Node,*pNode;

// 定义栈
typedef struct Stack
{
    pNode phead; // 栈顶指针
    int size; // 栈中的元素个数
}Stack,*pStack;

栈的操作：

初始化栈：

void init_stack(pStack stack)
{
    memset(stack, 0, sizeof(Stack));
}

入栈：

void push(pStack stack, ElemType val)
{
    pNode pnew = (pNode)calloc(1, sizeof(Node));
    pnew->data = val;

    if (!stack->phead)//栈为空
    {
        stack->phead = pnew;
    }

    else
    {
        pnew->next = stack->phead;
        stack->phead = pnew;
        stack->size++;
    }
}

出栈:

void pop(pStack stack)
{    
     pNode pcur=stack->phead;
    // 判断栈是否为空
    if(!stack->size)
    {
        printf("stack是空的！\n");
        return;
    }
    // 如果不为空
    stack->phead=pcur->next;
    stack->size--;
}

返回栈顶元素：

ElemType top(pStack stack)
{
   return stack->phead->data;
}

判断栈是否为空：

int isEmpty(pStack stack)
{
    return stack->size==0;
}

栈的大小:

int stack_size(pStack stack)
{
    return stack->size;
}

二、栈的应用

（一）数制转换

十进制数N和其他d进制数的转换原理： $N = (N \div d) \times d + N\mod d$

其中：div为整除运算，mod为求余运算

例如： $(1348)_{10}=(2504)_{8}$

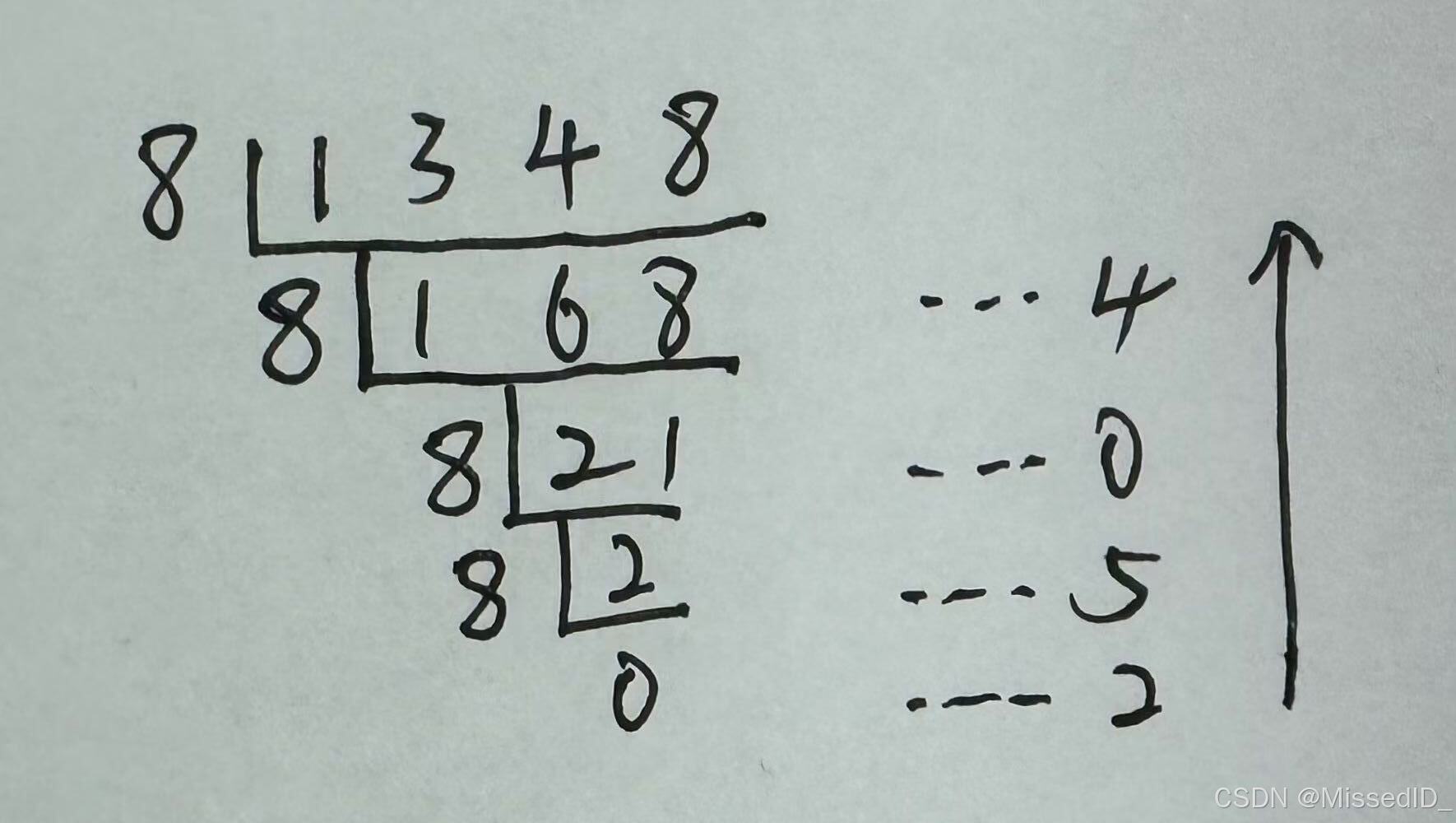
void conversion () 
{
// 对千输人的任意一个非负十进制整数，打印输出与其等值的八进制数   
     InitStack(S); 
     scanf ("%d",N);
     while (N) 
     {
          Push(S, N % 8);
          N = N/8;
     }
     while (!StackEmpty(S)) 
     {
          Pop(S,e);
          printf ( "%d", e );
     }
}

（二）括号匹配的检验

算法思想：

1）凡出现左括弧，则进栈；

2）凡出现右括弧，首先检查栈是否空

若栈空，则表明该“右括弧”多余，

否则和栈顶元素比较，

若相匹配，则“左括弧出栈” ，

否则表明不匹配。

3）表达式检验结束时，

若栈空，则表明表达式中匹配正确，

否则表明“左括弧”有余。

// 括号匹配检查
int check_parentheses(const char* expression) 
{
    Stack stack;
    init_stack(&stack);
    
    for (int i = 0; expression[i] != '\0'; i++) 
    {
        char current_char = expression[i];
        // 如果是左括号，入栈
        if (current_char == '(' || current_char == '{' || current_char == '[') 
        {
            push(&stack, current_char);
        }
        // 如果是右括号
        else if (current_char == ')' || current_char == '}' || current_char == ']') 
        {
            if (isEmpty(&stack)) 
            {
                return 0; // 右括号多余
            }
            char top_char = pop(&stack);
            // 检查是否匹配
            if ((top_char == '(' && current_char != ')') ||
                (top_char == '{' && current_char != '}') ||
                (top_char == '[' && current_char != ']')) 
            {
                return 0; // 括号不匹配
            }
        }
    }
    
    return isEmpty(&stack) ? 1 : 0; // 1表示匹配正确，0表示不匹配
}

（三）行编辑程序问题

当用户发现刚刚键入的一个字符是错的时，可补进一个退格符"#'，以表示前一个字符无效；如果发现当前键入的行内差错较多或难以补救，则可以键入一个退行符＂＠“，以表示当前行中的字符均无效。

为此，可设这个输入缓冲区为一个栈结构，每当从终端接受了一个字符之后先作如下判别：如果它既不是退格符也不是退行符，则将该字符压入栈顶；如果是一个退格符，则从栈顶删去一个字符；如果它是一个退行符，则将字符栈清为空栈。

while(ch != EOF) 
{ // EOF为全文结束符
    while (ch != EOF && ch != '\n') 
    {
        switch (ch) 
        {
        case '#': Pop(S, c); break;
        case '@': ClearStack(S); break; // 重置S为空栈
        default: Push(S, ch);  break;
        }
        ch = getchar();  // 从终端接收下一个字符
    }
    // 将从栈底到栈顶的字符传送至调用过程的数据区；
    ClearStack(S);      // 重置S为空栈
    if (ch != EOF)  ch = getchar();
}

（四）迷宫求解

求迷宫中从入口到出口的所有路径是一个经典的程序设计问题。由于计算机解迷宫时通常用的是＂穷举求解＂的方法，即从入口出发，顺某一方向向前探索，若能走通，则继续往前走；否则沿原路退回，换一个方向再继续探索，直至所有可能的通路都探索到为止。为了保证在任何位置上都能沿原路退回，显然需要用一个后进先出的结构来保存从入口到当前位置的路径。因此，在求迷宫通路的算法中应用“栈" 也就是自然而然的事了。

注意：所求路径必须是简单路径，即在求得的路径上不能重复出现同一通道块。

求迷宫中一条路径的算法的基本思想是：若当前位置“可通”，则纳入“当前路径”，并继续朝“下一位置”探索，即切换“下一位置”为“当前位置”，如此重复直至到达出口；若当前位置“不可通”，则应顺着“来向”退回到“前一通道块”，然后朝着除“来向”之外的其他方向继续探索；若该通道块的四周4个方块均“不可通”则应从“当前路径”上删除该通道块。假设以栈S记录“当前路径”，则栈顶中存放的是“当前路径上最后一个通道块”。由此，“纳入路径”的操作即为“当前位置入栈”；“从当前路径上删除前一通道块”的操作即为“出栈”。

注意：

1.当前位置，指的是在搜索过程中某一时刻所在图中某个方块位置。

2.下一位置，指的是“当前位置”四周4个方向（东、南、西、北）上相邻的方块。

3.当前位置可通，指的是未曾走到过的通道块，即要求该方块位置不仅是通道块，而且既不在当前路径上（否则所求路径就不是简单路径），也不是曾经纳入过路径的通道块（否则只能在死胡同内转圈）。

typedef struct {
	int ord;		// 通道块在路径上的＂序号” 
	PosType seat;   // 通道块在迷宫中的“坐标位置”
	int di;			// 从此通道块走向下一通道块的“方向”（可以表示东南西北）
}SElemType;			// 栈的元素类型

Status MazePa七h(MazeType maze, PosType start， PosType end)
{
	// Pass(curpos) : 检查当前位置是否可以通行。
	// FootFrint(curpos):记录走过的路径。
	// MarkPrint(e.seat):标记当前位置并打印出该位置的状态
	// 若迷宫 maze 中存在从入口 start 到出口 end 的通道，则求得一条存放在栈中（从栈底到栈顶），并返回 TRUE; 否则返回 FALSE
		
		InitStack(S); 
		curpos = start; // 设定“当前位置”为“入口位置”
		curstep = 1;	// 探索第一步
		do {
				if (Pass(curpos))  // 当前位置可以通过，即是未曾走到过的通道块
				{ 
					FootFrint(curpos); // 留下足迹
					e = (curstep, curpos, 1); // 将当前步数、坐标和方向初始化
					Push(S, e);		  //  将当前位置加入路径
					if (curpos == end) return (TRUE）; // 到达终点（出口）
					curpos = NextPos(curpos, 1); // 下一位置是当前位置的东邻
					curstep++; // 探索下一步
				} // if
				else  // 当前位置不能通过
				{
					if (!StackEmpty(S)) 
					{
						Pop(S,e);
						while(e.di == 4 && !StackEmpty(S))
						{
							MarkPrint(e.seat）; 
							Pop(S, e);
						} // while
						if (e.di < 4) 
						{
							e.di++; 
							Push(S,e);
							curpos = NextPos(e.seat,e.di);
						} // if
					}// if
				} //else
		} while (!StackEmpty(S));
		return (FALSE);
}

（五）表达式求值

限于二元运算符的表达式定义:

表达式 = (操作数) + (运算符) + (操作数)

操作数 = 简单变量 | 表达式

简单变量 = 标识符 | 无符号整数

表达式的三种标识方法：

设 Exp = S1 + OP + S2

OP + S1 + S2 为前缀表示法

S1 + OP + S2 为中缀表示法

S1 + S2 + OP 为后缀表示法

结论

（1）操作数之间的相对次序不变，运算符的相对次序不同;

（2）前缀式的运算规则为: 连续出现的两个操作数和在它们之前且紧靠它们的运算符构成一个最小表达式;

（3）中缀式丢失了括弧信息，致使运算的次序不确定;

（4）后缀式的运算规则为: 运算符在式中出现的顺序恰为表达式的运算顺序;每个运算符和在它之前出现且紧靠它的两个操作数构成一个最小表达式。

重点1：从后缀式求值->先找运算符，再找操作数

重点2：从原表达式求得后缀式

从原表达式求得后缀式的规律为：
1）设立运算符栈;
2）设表达式的结束符为“#”，预设运算符栈的栈底为“#”;
3）若当前字符是操作数，则直接发送给后缀式;
4）若当前运算符的优先数高于栈顶运算符，则进栈;
5）否则，退出栈顶运算符发送给后缀式；
6）“(”对它之前后的运算符起隔离作用，“)”可视为自相应左括弧开始的表达式的结束符。