《LeetCode之每日一题》:156.环形链表

最新推荐文章于 2025-08-24 13:00:45 发布

原创最新推荐文章于 2025-08-24 13:00:45 发布 · 116 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#链表 #leetcode #c++

LeetCode 专栏收录该内容

288 篇文章

订阅专栏

本文介绍四种检测链表中是否存在环的方法：利用数据范围漏洞、原地标记、哈希表及快慢指针法，并分析了每种方法的时间与空间复杂度。

环形链表

有关题目
- 题解

题目链接：环形链表

有关题目

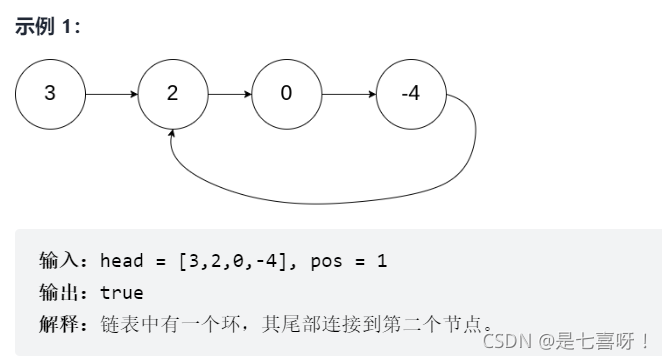
给定一个链表，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。
为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 
如果 pos 是 -1，则在该链表中没有环。
注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。 否则，返回 false 。

进阶：

你能用 O(1)（即，常量）内存解决此问题吗？

在这里插入图片描述

提示：

链表中节点的数目范围是 [0, 10^4]
-10^5 <= Node.val <= 10^5
pos 为 -1 或者链表中的一个 有效索引 。

题解

Tips
map,unordered_map,set和unordered_set的用法和区别

注意本题用unordered_map参数太少了，我们只需要存储节点，故使用unordered_set就可以了

法一：利用题目数据范围漏洞
参考官方题解评论区下arttnba3

思路：无环的链表节点数最多为10000，而有环的链表则，则可以循环1w 次以上

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if (head == nullptr || head->next == nullptr) return false;
        int n = 0;
        while(head != nullptr){
            head = head->next;
            ++n;
            if (n > 10000) return true;
        }
        return false;
    }
};

时间复杂度：O(n), n 为链表的长度
空间复杂度：O(1)
法二：原地标记
参考官方题解评论区下Lam

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
    const int flag = 1e5 + 1;
public:
    bool hasCycle(ListNode *head) {
        if (head == nullptr || head->next == nullptr) return false;
        while(head != nullptr){
            if (head->val == flag) return true;
            head->val = flag;
            head = head->next;
        }
        return false;
    }
};

时间复杂度：O(n)，n 为链表长度
空间复杂度：O(1)，不破坏链表则需要拷贝,空间复杂度仍为O(n)
法三：哈希表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        unordered_set<ListNode*> mp;
        while(head != nullptr){
            if (mp.count(head)){
                return true;
            }
            mp.insert(head);
            head = head->next;
        }
        return false;
    }
};

在这里插入图片描述
法四：快慢指针
参考官方题解

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if (head == nullptr || head->next == nullptr) return false;
        ListNode* fast = head->next, *slow = head;
        while(fast != slow){
            if (fast == nullptr || fast->next == nullptr) return false;
            fast = fast->next->next;
            slow = slow->next;
        }
        return true;
    }
};