《LeetCode之每日一题》:12. 搜索二维矩阵

题目链接： 搜索二维矩阵

有关题目

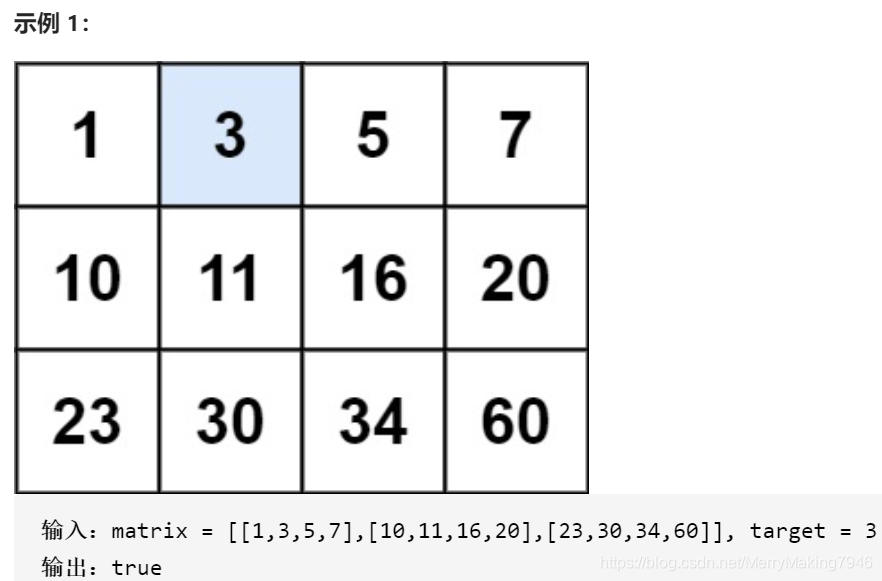
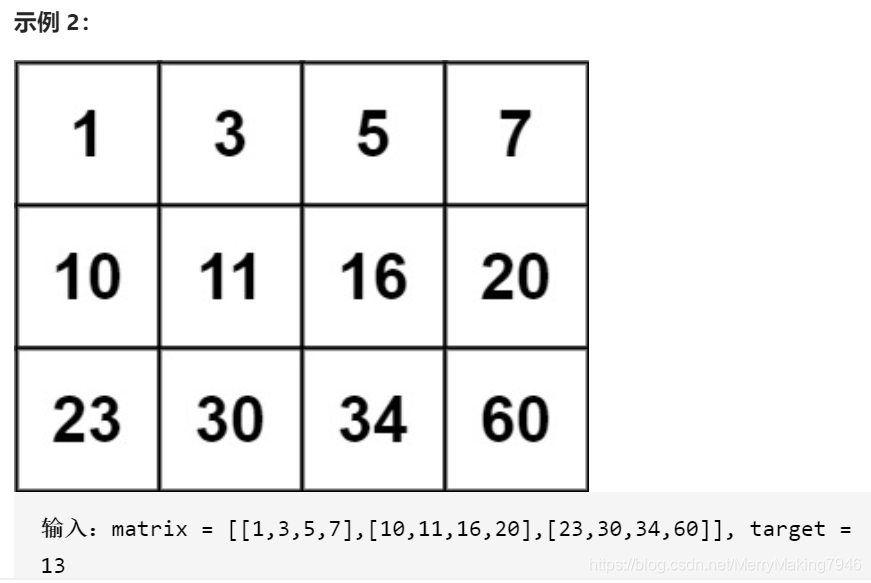
编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。
该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

提示：
m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-10^4 <= matrix[i][j], target <= 10^4

题解

1、暴力法

bool searchMatrix(int** matrix, int matrixSize, int* matrixColSize, int target)
{
	int x,y;
	for (x = 0; x < matrixSize; x++)
	{
		for ( y = 0 ; y < * matrixColSize; y++)
		{
			if (matrix[x][y] == target)
				return true;
		}
	}
	//
	return false;
}

时间复杂度： O(M * N)
空间复杂度：O(1)
2、查找所在行1

bool searchMatrix(int** matrix, int matrixSize, int* matrixColSize, int target){
   int i,j;
   for (i = 0; i < matrixSize; i++)
   {
       for(j = *matrixColSize - 1; j >= 0; j--)
       {
           if (matrix[i][j] < target)
                break;
            if (matrix[i][j] == target)
                return true;
       }
   }
        return false;
}

时间复杂度：O(M * N)
空间复杂度：O(1)

3、寻找到所在行2

bool searchMatrix(int** matrix, int matrixSize, int* matrixColSize, int target){
    int y = *matrixColSize - 1;
    for (int i = 0; i < matrixSize; i++)
        {
            if (matrix[i][y] < target)
                continue;
            else if (matrix[i][y] == target)
                return true;
            else
                {
                    for (int j = y - 1; j >= 0; j--)
                    {
                        if (matrix[i][j] == target)
                            return true;
                    }
                }
                //行内使用二分查找
			//int right = y - 1;
            //        int left = 0;
            //        while(right >= left)
            //            {
             //               int mid = (left + right) / 2;
             //               if (matrix[i][mid] > target)
             //                   right = mid - 1;
             //               else if (matrix[i][mid] < target)
               //                 left = mid + 1;
              //              else
               //                 return true;
              //          }
        }
        return false;
}

时间复杂度： 在行中遍历查找的时间复杂度是： O(M + N)；如果在行中进行二分查找的时间复杂度是则 O(M + log(N))
空间复杂度：O(1)

4、跟搜索二维矩阵 II相类似

bool searchMatrix(int** matrix, int matrixSize, int* matrixColSize, int target){
    int x = 0;
    int y = *matrixColSize - 1;
    while(y >= 0 && x < matrixSize )
    {
        if (matrix[x][y] > target)
            y--;
        else if (matrix[x][y] < target)
            x++;
        else
            return true;
    }
        return false;
}

时间复杂度：O(M + N)
空间复杂度：O(1)

5、
两次二分查找

bool searchMatrix(int** matrix, int matrixSize, int* matrixColSize, int target){
    int m = matrixSize;
    int n = *matrixColSize;
    //先查找行
    int l = 0;
    int r = m - 1;
    while(l < r)
    {
        int mid = l + r + 1 >> 1;
        if (matrix[mid][0] <= target)
            l = mid;
        if (matrix[mid][0] > target)
            r = mid - 1;
    }
    //出来判断
    if (matrix[r][0] == target) return true;
    if (matrix[r][0] > target) return false;
    int row = r;
    //比较列
    l = 0;
    r = n - 1;
    while(l < r)
    {
        int mid = l + r + 1 >> 1;
        if (matrix[row][mid] <= target)
            l = mid;
        if (matrix[row][mid] > target)
            r = mid - 1;
    }   
    int col = r;
    return matrix[row][col] == target;
}

时间复杂度：O(logM + logN)
空间复杂度：O(1)

6、全局查找的二分查找

bool searchMatrix(int** matrix, int matrixSize, int* matrixColSize, int target){
    int m = matrixSize;
    int n = *matrixColSize;
    int l = 0;
    int r = m * n - 1;
    //这边其实也包含了
    //[1]
    //查找1这种情况，因为根本就进不去循环
    while(l < r)
    {
        int mid = l + r + 1 >> 1;
        if (matrix[mid / n][mid % n] <= target)
            l = mid;
        if (matrix[mid / n][mid % n] > target)
            r = mid - 1;
    }
     return matrix[r / n][r % n] == target;
}

时间复杂度：O(log(M * N)
空间复杂度：O(1)