Open Cascade 8.0.0 新增模块：TKHelix 螺旋线工具

模块功能

2025年7月29日 Open CASCADE 在 8.0.0 RC 候选发布版本中新增了 TKHelix 模块，用于生成由解析式定义的圆柱螺旋线、带锥度的圆锥螺旋线，主要功能有：

构造螺旋曲线适配器 Adaptor3d_Curve。这里有个疑问——OCC开发者为什么不像定义椭圆、圆曲线那样，将螺旋线定义为 Geom_Curve链接，而是将其定义为适配器曲线？稍后再来讨论该问题。
构造螺旋线拓扑模型；
将螺旋线拟合为 B 样条曲线。

圆柱螺旋定义

螺旋线可理解为一点绕回转轴做匀速旋转运动、沿轴线方向做平移运动这两个运动的合成运动轨迹，参数化方程为：
$\mathbf C(t)=(x(t), y(t), z(t)), \begin{cases} x(t)= r(t) \cdot cos(t) \\ y(t) = r(t) \cdot sin(t) \cdot directionSign \\ z(t) = pitch \cdot \frac t {2\pi} \end{cases}$
其中，

$r(t)=rStart+taperFactor\cdot t$
$t$ 为曲线参数，几何含义为绕旋转轴旋转的角度；
$t a p er F a c t or$ 为锥度因子，每旋转一圈半径的变化量。若设圆锥顶角为 $\alpha$ ，可得： $tan(\frac \alpha 2)\cdot pitch=taperFactor \cdot 2\pi$ ，如下图所示。注意，OCC中使用半锥角，而且两处实现分别使用锥度因子和半锥角，不知道为什么要这么麻烦的处理。
$r (t)$ 表示生成螺旋线轨迹的旋转半径，它随着旋转角度的变化而变化；当因子 $t a p er F a c t or$ 为 0 时， $r (t)$ 为固定值，此时曲线 $\mathbf C(t)$ 表示为圆柱螺旋；
$d i rec t i o n S i g n$ 表示螺旋的方向，默认逆时针旋转；
$p i t c h$ 表示螺距， $r St a r t$ 初始螺旋半径。
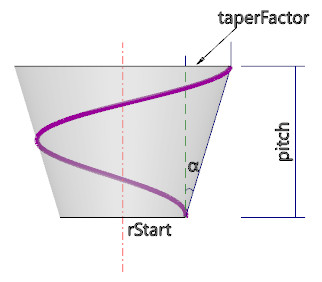
这就是 TKHelix 螺旋线的定义方式。

运行效果

① $rStart=10，pitch=5，tapperFactor=0，directionSign=逆时针，t\in[0, 6\pi]$
在这里插入图片描述
② $rStart=10，pitch=12，tapperFactor=0，directionSign=逆时针，t\in[0, 6\pi]$

③ $rStart=10，pitch=12，tapperFactor=1，directionSign=逆时针，t\in[0, 6\pi]$
在这里插入图片描述

④ $rStart=20，pitch=12，tapperFactor=5，directionSign=逆时针，t\in[0, 6\pi]$
在这里插入图片描述

OCC 实现

模块业务逻辑

模块主要对外接口是HelixGeom_Tools、HelixGeom_BuilderHelix、HelixBRep_BuilderHelix，分别得到几何模型、拓扑模型，如下图所示：

螺旋线的其他实现1——Geom_HelixCurve方法

对于这种螺旋，还有另一种更为直接、简单的方法，如下图所示：

这种方式我在几年前曾实现过[源代码]，仅支持构造圆柱螺旋，当然也可扩展支持锥度。Geom_HelixCurve所定义的圆柱螺旋线可适用于OCC所有的几何、拓扑算法。

螺旋线的其他实现2——BRep_CurveOnSurface方法

圆柱螺旋、圆锥螺旋或位于其他回转面上的螺旋线，可以看作位于曲面上的一条面上曲线，即构造 BRep_CurveOnSurface，如下图所示：
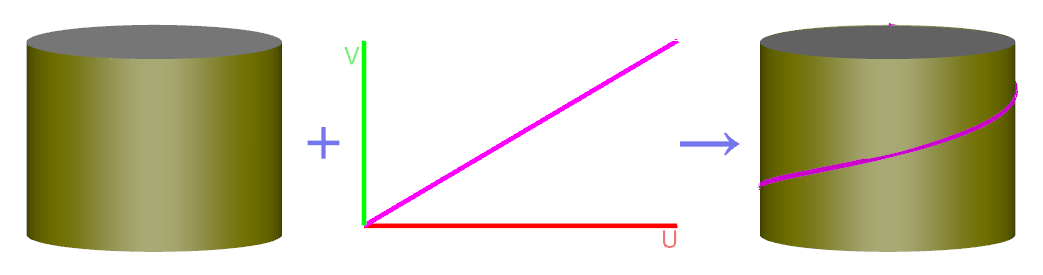
在这里插入图片描述
详细可参考 eryar 的博客。

不同实现对比

OCC为什么不采用这种简单的方式? 当我第一次看到 OCC 官方实现的圆柱螺旋算法时，第一印象便是疑惑、感到复杂，也就是本文开头所讲的，OCC开发者为什么不像定义椭圆、圆曲线那样，将螺旋线派生自 Geom_Curve，而是将其定义为适配器曲线？通过对比自己的实现和OCC的实现，似乎能找到一些原因。

① 对于空间任意位置的螺旋线，我实现的版本在每次获取曲线属性（如D0, D1, D2等）时，都必须执行一次变换（成员变量 lcs），这种处理在一些数值算法迭代求解过程中可能消耗更多的时间。而将其转换为 B 样条曲线之后，则不存在这样的问题。

② 将曲线派生自 Adaptor3d_Curve而不是 Geom_Curve可以在一定程度上避免被滥用，因为通常情况下，相比于Adaptor3d_Curve开发者更倾向于使用 Geom_Curve，一旦出现 Geom_HelixCurve开发者可能会优先使用。

③ OCC中的算法一般情况下，虽然可同时接收 Adaptor3d_Curve和 Geom_Curve作为输入，而当 HelixGeom_HelixCurve仅支持绕 OZ 轴的螺旋线时，受制于这样的场景限制，开发者可能被迫选择使用HelixGeom_BuilderHelix，即得到一条的 B 样条曲线而非参数化定义的螺旋线，避免因使用不当而低效。

④ 派生自 Geom_Curve的一些二次曲线，OCC中是否转换成了 B样条曲线？如果同样使用类似HelixGeom_HelixCurve的方式做处理，又是否会提高一些算法的效率？这里挖个坑，之后再专门研究。

当然，以上仅仅是我的一些猜测，欢迎提出质疑。

接下来针对以上不同实现，测试对比性能。

性能对比

在线-线距离、线-面求交两个场景下对比以上三种方法的性能，测试时三种方法按随机顺序执行N次，取平均值。

场景\耗时(ms)	OCC 方法	Geom_HelixCurve 方法	BRep_CurveOnSurface 方法
线-线距离	24.4094	22.2883	27.113
线-面求交	1.68902	1.48758	1.86857

从以上测试可以看出，HelixGeom_BuilderHelix、Geom_HelixCurve和BRep_CurveOnSurface三种方法效率没有明显差异。由于HelixGeom_BuilderHelix中bug的存在（参考下边的 Bug 章节），测试结果仅供参考，实际的性能表现还需要在具体场景中具体分析。

对于二次曲面或其他参数化曲面，如果同样将其拟合为B样条曲面，一些算法的效率是否会得到提升？这里挖一个坑，后续填上。

Bug

B样条拟合问题

在进行测试时，由HelixGeom_BuilderHelix得到的曲线不是螺旋线，而HelixGeom_HelixCurve是可以正确表达一个螺旋线的。如下图所示，使用同一组参数( $t\in[0, 2\pi], pitch=5, rStart=10, taperFactor=0)$ 构造螺旋线，洋红色是HelixGeom_HelixCurve曲线上采样点连接而成的多边形，浅灰色是HelixGeom_BuilderHelix得到的B样条曲线，可以看出后者的明显错误。这个问题可能因为B样条拟合时出错导致，或许之后需要详细调试一下。
在这里插入图片描述

顺逆时针标志代码错误

查看HelixGeom_HelixCurve源码如下：

gp_Pnt HelixGeom_HelixCurve::Value(const Standard_Real aT) const
{
  Standard_Real aST, aCT, aX, aY, aZ, a1;
  // Calculate trigonometric values and radius
  aCT = cos(aT);
  aST = sin(aT);
  a1  = myRStart + myC1 * myTgBeta * aT;
  // Calculate Cartesian coordinates
  aX = a1 * aCT;
  aY = a1 * aST;
  if (!myIsClockWise)
  {
    aY = -aY;
  }
  aZ = myC1 * aT;
  return gp_Pnt(aX, aY, aZ);
}

其中aX = a1 * aCT; aY = a1 * aST; 为逆时针旋转aT角度后的坐标值，而if (!myIsClockWise) { aY = -aY; }表示顺时针时、Y坐标值应反向。因此myIsClockWise的取值应是逆时针为true、顺时针为false。即变量应重命名为 myIsCounterClockWise。

实现不完整

HelixGeom_HelixCurve派生自Adaptor3d_Curve，但其中一个如下的虚函数（非纯虚）未实现，一些以Adaptor3d_Curve为输入、按曲线类型分情况处理的算法，不能接收螺旋线HelixGeom_HelixCurve，例如，求曲线长度方法GCPnts_AbscissaPoint::Length。

  //! Returns  the  type of the   curve  in the  current
  //! interval :   Line,   Circle,   Ellipse, Hyperbola,
  //! Parabola, BezierCurve, BSplineCurve, OtherCurve.
  Standard_EXPORT virtual GeomAbs_CurveType GetType() const;

当然，这或许也复合该模块的设计初衷——HelixGeom_HelixCurve不对外使用，只不过缺少一些防错处理。

以上这些问题后续找时间反馈给开源社区。