数据结构-C语言描述（树）

概述

我们先回顾一下常见的物理结构，包括：集合结构、线性结构、树状结构和图结构。而从树状结构开始数据元素之间的关系就不是简单的一对一了，变成了一对多或者多对多，简而言之就是元素之间关系变得更加复杂了。而我们今天要学习的就是典型的一种一对多的物理结构——树状结构。

首先我们通过一棵生活中常见的树来建立一个树的整体概念：

我们来观察一下， 从树根开始慢慢往上，发现逐渐由新的分支出现，而且分支上还可能会有分支。此时我们思考一下生活中有怎样的数据与树的结构相同？

例如图书馆中书籍的分类：

我们先想一下我们如何在图书馆中找到我们需要的那本书？

• 首先要知道它在几楼
• 然后明确它在某楼的几号阅览室
• 在知道它在某号阅览室的几排书架
• 然后是该书架的第几排
• 这排的第几本

我们将这个步骤与树状结构联系起来：一个分叉点会有多个分支，相对应的，一楼会有多个阅览室、一个阅览室会有多排书架……

由此可见，树状结构的物理结构在生活中的应用还是比较广泛的。

1.树的相关概念

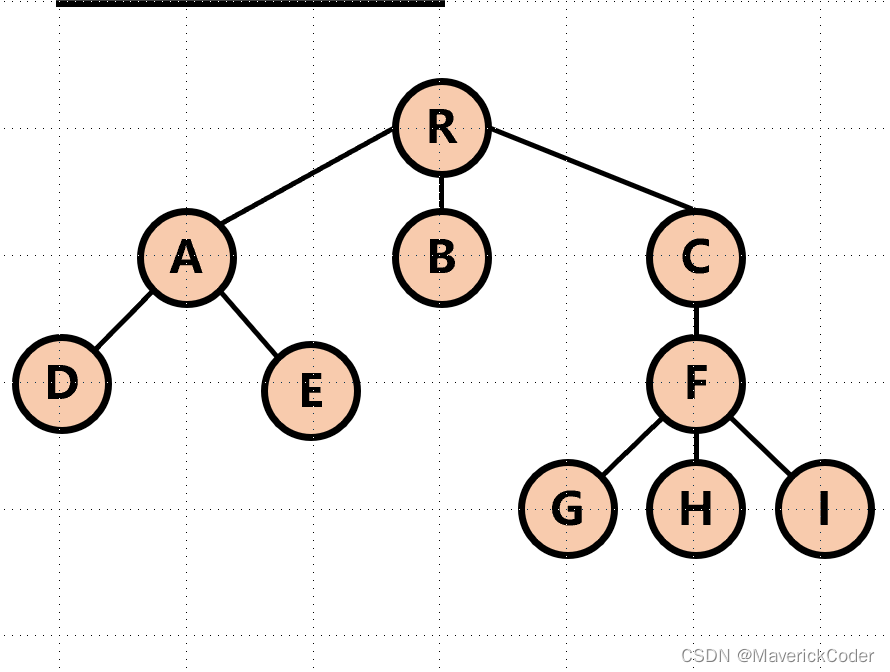
树的度数

 看图我们发现，图中的这棵树很规律的分为了四层，我们称这棵树的度数为4。

结点

我们如果通过关系将结点分类的话，可分为两类（parentNode和childNode）。

以这张图为例，下结点是有直接联系的上层结点的子结点（A、B、C都是R的子结点；D、E都是A的子结点）。又有，同一结点的子结点互为兄弟结点（G、H、I互为兄弟结点）。 

如果根据度数分类的话，可分为三类根结点root（该图中R）、叶子结点leafNode（无子结点的结点D、E、I）、普通结点（A、B、C、F）。

2.链表结点的创建

首先先将头文件和宏文件写好：

#include <stdio.h>
#include <stdlib.h>
#define eletype char

 这里我们使用链表来连接相关结点，所以我们定义一个结构体ListNode：

struct TreeNode;  //因为在定义ListNode的时候要用到TreeNode，所以在这先定义一下
typedef struct ListNode {
    struct TreeNode* data;  //ListNode是一个记录TreeNode的链表，*data用来记录树结点的数据
    struct ListNode *next;  //*next用来指向下一个记录TreeNode链表
} ListNode;

3.树结点的创建

树结点应该包括数据域data和该结点下的子结点链表*childNode

typedef struct TreeNode {
    eletype data;            //数据域data用来记录树结点中的数据
    ListNode *childrenHead;  //*childHead用来记录该结点下的子结点链表
} TreeNode;

4.添加树边

因为树结点间的特殊关系，我们通常要将两个树结点（一般是结点与它的子结点）之间建立联系（称之为添加树边）。而要完成这一步我们首先要将参数传入，包括parentNode和childNode：

void AddTreeChild (TreeNode* parent,TreeNode* child) {
    ListNode *childNode=(ListNode*)malloc(sizeof(ListNode));
    childNode->data=child;     //新定义一个结点childNode来接收child
    childNode->next=NULL;      //然后将其*next置空
    if(parent->childrenHead==NULL){      //先判断母结点的孩子结点链表是否为空
        parent->childrenHead=childNode;  //若为空，则直接将childNode作为子链表头指针
    } else {
        childNode->next=parent->childrenHead; //注意这里用的都是头插法
        parent->childrenHead=childNode;
    }
}

5.树结构体的定义

然后我们需要整棵树的框架（即用类型为TreeNode的一个数组nodes来记下每个树结点）：

typedef struct Tree {
    TreeNode *nodes;   //用来储存树结点
    TreeNode *root;
} Tree;

6.树的创建

我们先要清楚创建树时，需要初始化的仅有在Tree中定义的*node和*root，我们之前定义的结构是会包括在*node里的：

void TreeCreat (Tree* t,int size) {
    t->nodes=(TreeNode*)malloc(sizeof(TreeNode)*size);   //先让*node指向空
    t->root=NULL;   //*root也指向空
}

7.树的销毁

void TreeDestroy (Tree* t) {
    free(t->nodes);  //将*node树的空间释放掉
    t->nodes=NULL;  //然后将两个指针置空
    t->root;
}

8.获取树结点

TreeNode* GetTreeNode (Tree* t,int ID) {
    return &t->nodes[ID];
}

9.给树结点添加边

这一步只需要将要添加的两结点传入，并且调用AddTreeChild函数添加：、

void TreeAddChild (Tree* t,int parentId,int childId) {
    TreeNode* parentNode=GetTreeNode(t,parentId);
    TreeNode* childNode=GetTreeNode(t,childId);
    AddTreeChild(parentNode,childNode);
}

10.设置根结点

void TreeAssignRoot (Tree* t,int Id) {
    t->root=GetTreeNode(t,Id);    //调用TreeGetNode函数找到目标结点
}                                 //然后将该结点赋给*root

11.设置结点值

先要将结点值传入，然后找到要赋值的结点：

void TreeAssignData (Tree* t,int Id,eletype value) {
    GetTreeNode(t,Id)->data=value;
}

12.深度优先遍历（简化篇）

深度优先遍历是一种常见的遍历方法，举个例子，

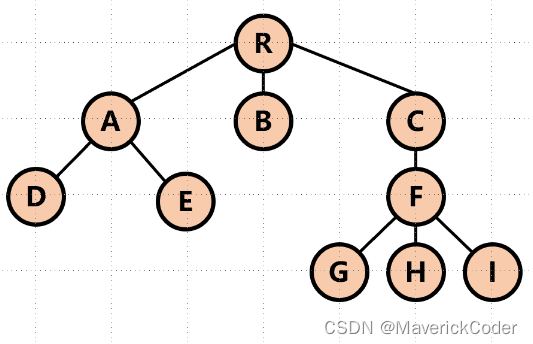
 若以根结点R为起点，进行深度优先遍历，其路径为R->A->D。即在搜索的过程中，查找下一个节点的原则是往树的更深处查找。如果想深入了解深度优先遍历的过程可以参考离散数学图的遍历。

void TreePrint (Tree* t,TreeNode* node) {
    if(node=NULL){
        node=t->root;
    } 
    printf("%c",node->data);
    ListNode* tmp=node->childrenHead;
    while(tmp){
        TreePrint(t,tmp->data);
        tmp=tmp->next;
    }
    
}

完整源码

#include <stdio.h>
#include <stdlib.h>

#define eletype char

struct TreeNode;

typedef struct ListNode {
	struct TreeNode* data;
	struct ListNode* next;
} ListNode;

typedef struct TreeNode {
	eletype data;
	ListNode *childrenHead;
} TreeNode;

void AddTreeChild(TreeNode *parent,TreeNode *child){
	ListNode* childNode=(ListNode*)malloc(sizeof(ListNode));
	childNode->next=NULL;
	childNode->data=child;
	if(parent->childrenHead==NULL){
		parent->childrenHead=childNode;
	} else {
		childNode->next=parent->childrenHead;
		parent->childrenHead=childNode;
	}
}

typedef struct Tree{
	TreeNode *nodes;
	TreeNode *root;
} Tree;

void TreeCreat (Tree *t,int size){
	t->nodes=(TreeNode*)malloc(sizeof(TreeNode)*size);
	t->root=NULL;
}

void TreeDestroy (Tree *t){
	free(t->nodes);
	t->nodes=NULL;
	t->root=NULL; 
}

TreeNode* TreeGetNode(Tree *t,int id){
	return &t->nodes[id];
}

void TreeSetRoot (Tree* t,int id){
	t->root=TreeGetNode(t,id);
}

void TreeAddChild(Tree* t,int parentID,int childID){
	TreeNode* parentNode=TreeGetNode(t,parentID);
	TreeNode* childNode=TreeGetNode(t,childID);
	AddTreeChild(parentNode,childNode);
}

void TreeAssignData(Tree* t,int id,eletype data){
	TreeGetNode(t,id)->data=data;
}

void TreePrint(Tree* t,TreeNode *node){
	if(node==NULL){
		node=t->root; 
	} 
	printf("%c",node->data);
	ListNode *tmp=node->childrenHead;
	while(tmp){
		TreePrint(t,tmp->data);
		tmp=tmp->next;
	}
}

int main(){
	Tree T;
	TreeCreat(&T,9);
	TreeSetRoot(&T,0);

	TreeAssignData(&T,0,'a');
	TreeAssignData(&T,1,'b');
	TreeAssignData(&T,2,'c');
	TreeAssignData(&T,3,'d');
	TreeAssignData(&T,4,'e');
	TreeAssignData(&T,5,'f');
	TreeAssignData(&T,6,'g');
	TreeAssignData(&T,7,'h');
	TreeAssignData(&T,8,'i');
	
	TreeAddChild(&T,0,2);
	TreeAddChild(&T,0,1);
	TreeAddChild(&T,1,3);
	TreeAddChild(&T,2,5);
	TreeAddChild(&T,2,4);
	TreeAddChild(&T,3,8);
	TreeAddChild(&T,3,7);
	TreeAddChild(&T,3,6);
	
	TreePrint(&T,T.root);
	return 0; 
	
	
}

 后记

分布解析的代码好像有点小问题（思路没有问题），应该是有个小的细节错误，但是调试的时候没有找到。后面的完整源码是我重新敲得，没有问题，放心食用。那个小问题后面找到了，会将博客更新的。