1 简介
NSGA(非支配排序遗传算法)、NSGAII(带精英策略的非支配排序的遗传算法),都是基于遗传算法的多目标优化算法,都是基于pareto最优解讨论的多目标优化.







2 部分代码
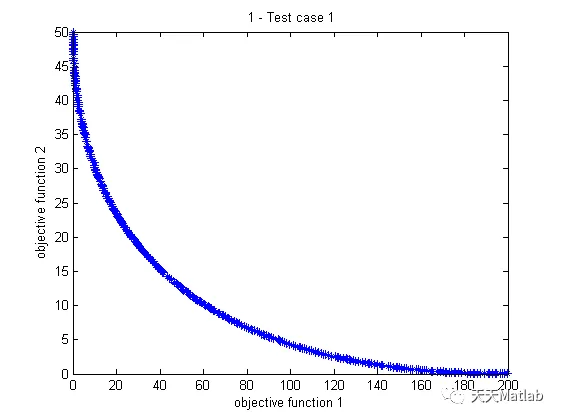
3 仿真结果
4 参考文献
[1]徐慧英等. "改进NSGA Ⅱ算法在车辆路径多目标优化问题中的应用." 计算机工程与科学 32.10(2010):117-121.

NSGA(非支配排序遗传算法)、NSGAII(带精英策略的非支配排序的遗传算法),都是基于遗传算法的多目标优化算法,都是基于pareto最优解讨论的多目标优化.








[1]徐慧英等. "改进NSGA Ⅱ算法在车辆路径多目标优化问题中的应用." 计算机工程与科学 32.10(2010):117-121.


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


