🔥 内容介绍
小波变换可用于脉搏信号去噪的目的。脉搏信号是一种包含大量噪声的生物信号,而小波变换可以通过将信号分解成不同频率的细节和近似部分来分析和处理信号。通过对细节部分进行阈值处理或滤波操作,可以去除噪声并保留有用的信号信息。
在小波变换中,信号首先与一组特定的小波基函数进行卷积,然后通过缩放和平移来表示不同频率的分量。通过选择适当的小波基函数和设置合适的阈值,可以消除脉搏信号中的噪声。
常用于脉搏信号去噪的小波基函数有以下几种:
-
Daubechies小波函数 (dbN):Daubechies小波函数是最常用的小波基函数之一。它具有紧凑的支持和快速衰减的特性,适用于信号的细节提取和去噪。
-
Symlet小波函数 (symN):Symlet小波函数是一种对称的小波基函数,类似于Daubechies小波函数。它在保持Daubechies小波函数特性的同时,具有更好的低频部分近似能力。
-
Coiflet小波函数 (coifN):Coiflet小波函数是一种具有紧凑支持和快速衰减特性的小波基函数。与Daubechies和Symlet小波函数相比,Coiflet小波函数更适用于信号中存在突变的情况。
-
Haar小波函数:Haar小波函数是最简单的小波基函数,它是一种非常紧凑的小波基函数。虽然它在信号细节提取方面效果较差,但在某些情况下仍然被用于脉搏信号去噪。
选择合适的小波基函数进行脉搏信号去噪需要考虑以下几个因素:
-
信号特性:首先要了解脉搏信号的频率范围、幅度范围以及信号的稳定性。不同的小波基函数适用于不同频率范围的信号。
-
小波基函数的性质:不同的小波基函数具有不同的时域和频域特性。有些小波基函数适合处理非平稳信号,而有些适合处理平稳信号。需要选择适合脉搏信号的非平稳或平稳小波基函数。
-
噪声类型:了解脉搏信号中可能存在的噪声类型,如高频噪声、低频噪声等。选择合适的小波基函数可以更好地抑制特定类型的噪声。
-
实际应用需求:考虑到实际应用需求,如去噪后信号的保真度、计算复杂度等。一些小波基函数在去噪效果上可能更好,但计算复杂度较高。
综上所述,选择合适的小波基函数需要综合考虑信号特性、小波基函数的性质、噪声类型和实际应用需求。
📣 部分代码
function data=Xnoise(d)d1=d(1:4000);[swa,swd]=swt(d1,5,'coif4');%计算等级N的信号X的平稳小波分解,使用'coif4'小波基。[thr,sorh]=ddencmp('den','wv',d1);dswd=wthresh(swd,sorh,thr);data=iswt(swa,dswd,'coif4');
⛳️ 运行结果
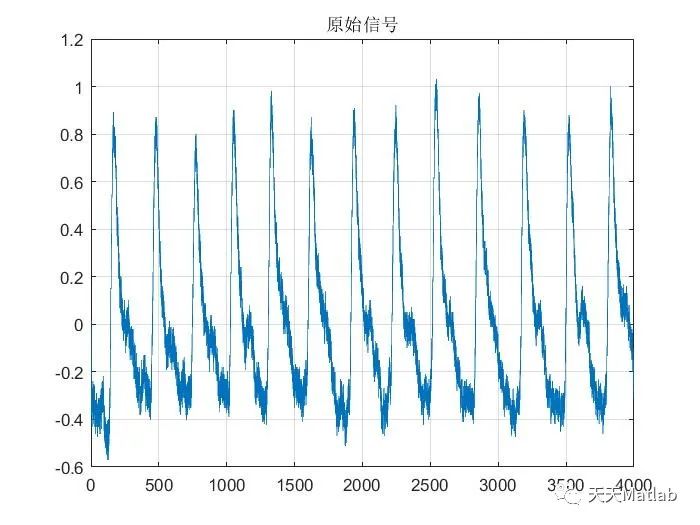

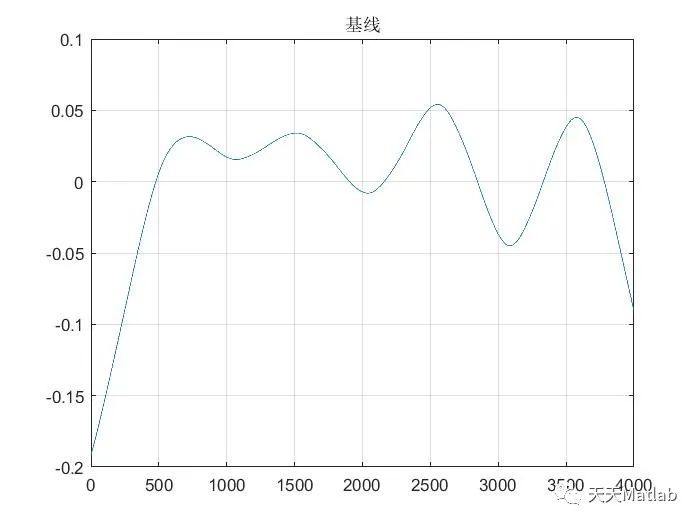
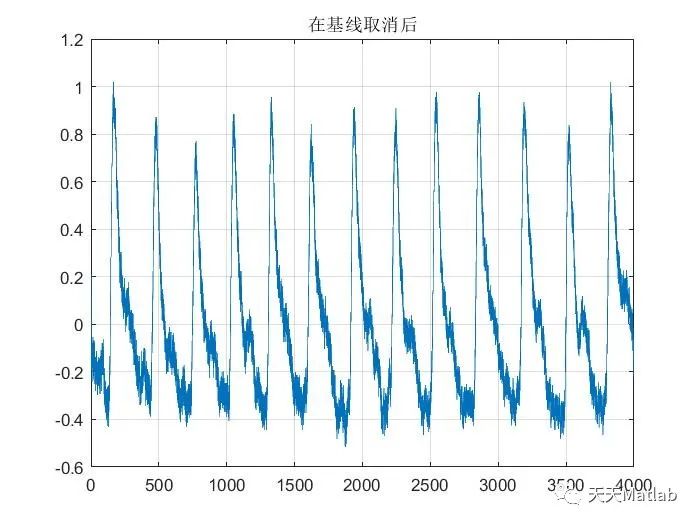
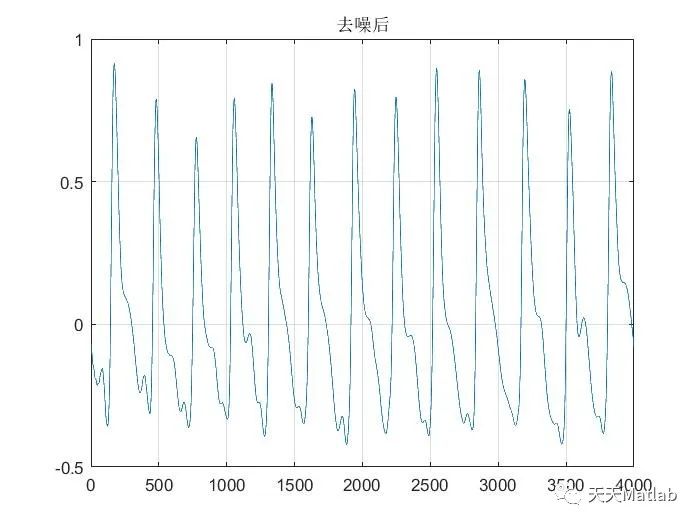
🔗 参考文献
[1]张丽琼,王炳和.基于小波变换的人体脉搏信号去噪处理[J].陕西师范大学学报:自然科学版, 2004(S1):3.DOI:CNKI:SUN:SXSZ.0.2004-S1-027.




 本文介绍了小波变换如何通过分解和处理脉搏信号中的不同频率成分来去除噪声。重点讨论了Daubechies、Symlet、Coiflet和Haar等多种小波基函数的选择原则,包括信号特性、小波性质、噪声类型和实际应用需求。
本文介绍了小波变换如何通过分解和处理脉搏信号中的不同频率成分来去除噪声。重点讨论了Daubechies、Symlet、Coiflet和Haar等多种小波基函数的选择原则,包括信号特性、小波性质、噪声类型和实际应用需求。
















 1143
1143

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








