【下垂控制与虚拟同步机】下垂控制与虚拟同步机两种并网型（grid-forming）控制策略的性能研究（Simulink仿真实现）

   💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文内容如下：🎁🎁🎁

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥第一部分——内容介绍

下垂控制与虚拟同步机两种并网型控制策略的性能研究

摘要

随着可再生能源大规模接入电网，并网型变流器（grid-forming converter）的动态特性对系统稳定性影响显著。本文基于5 MW变流器模型，通过MATLAB/Simulink仿真对比下垂控制（Droop Control）与虚拟同步机（Virtual Synchronous Machine, VSM）在功率阶跃响应、电网扰动下的暂态性能及稳态功率分配能力。结果表明：下垂控制响应速度快但存在稳态偏差，且缺乏惯性支撑；VSM通过引入转子运动方程，可模拟同步机惯性，显著提升系统抗扰能力，但需优化参数以避免过阻尼。研究为高比例新能源电网的并网控制策略选择提供理论依据。

关键词

下垂控制；虚拟同步机；并网型变流器；功率分配；惯性支撑

1 引言

传统同步发电机因转动惯量（H）和阻尼特性，在电网频率波动时通过释放动能维持稳定。然而，随着光伏、风电等新能源通过变流器大规模并网，电网惯性持续下降，频率稳定性面临挑战。并网型变流器需具备自主构建电压和频率的能力，其控制策略分为下垂控制与虚拟同步机两类：

• 下垂控制：模拟同步发电机一次调频特性，通过有功-频率（P-f）和无功-电压（Q-V）下垂曲线实现功率分配，无需通信，但本质为有差调节，缺乏惯性支撑。
• 虚拟同步机：在控制算法中嵌入转子运动方程，使变流器外特性等效于同步机，可提供虚拟惯性（J）和阻尼（D），增强系统抗扰能力。

本文基于5 MW变流器模型，对比两种策略在功率阶跃、电网扰动下的性能差异，分析其适用场景及优化方向。

2 模型与方法

2.1 仿真模型配置

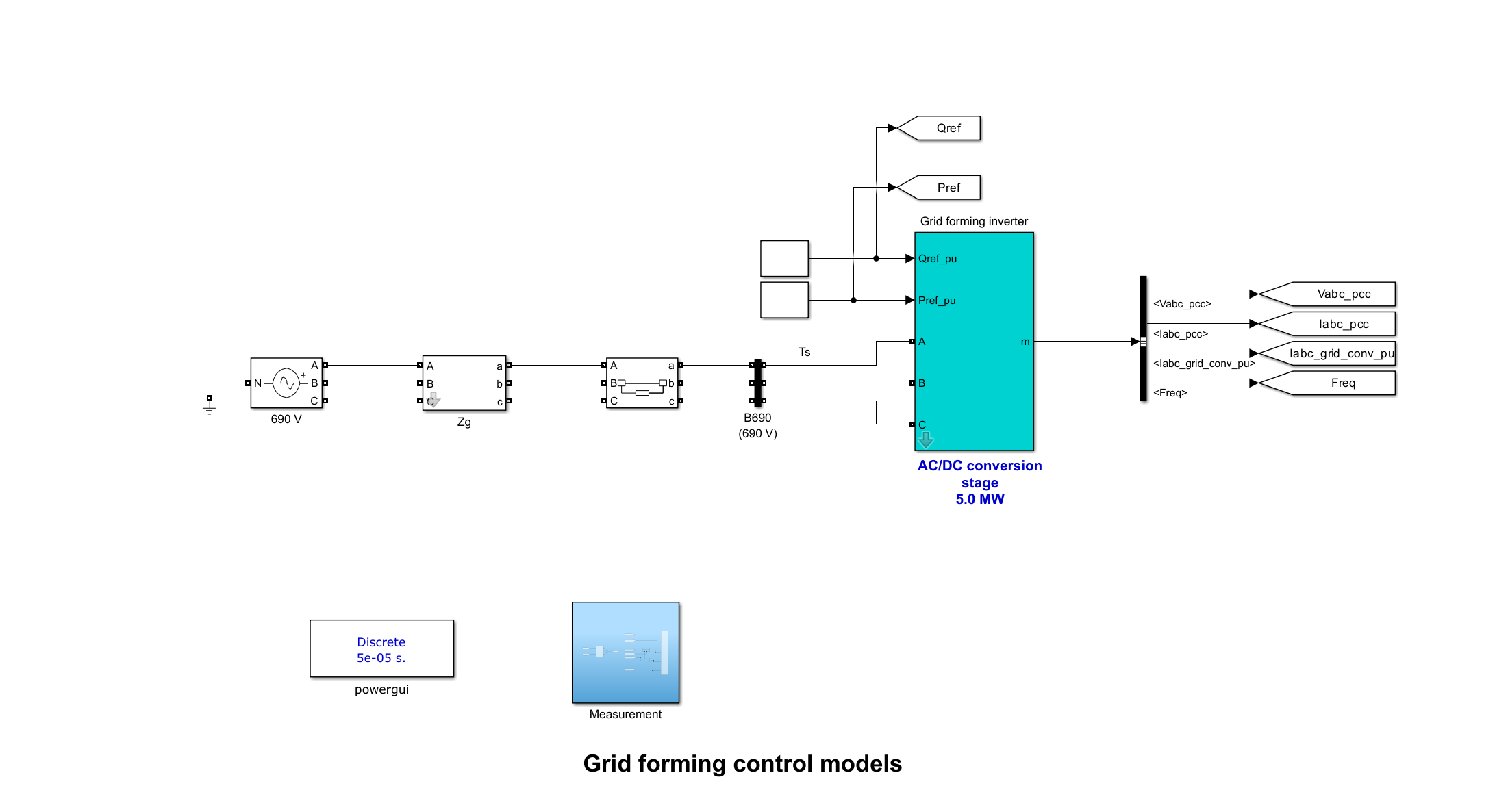
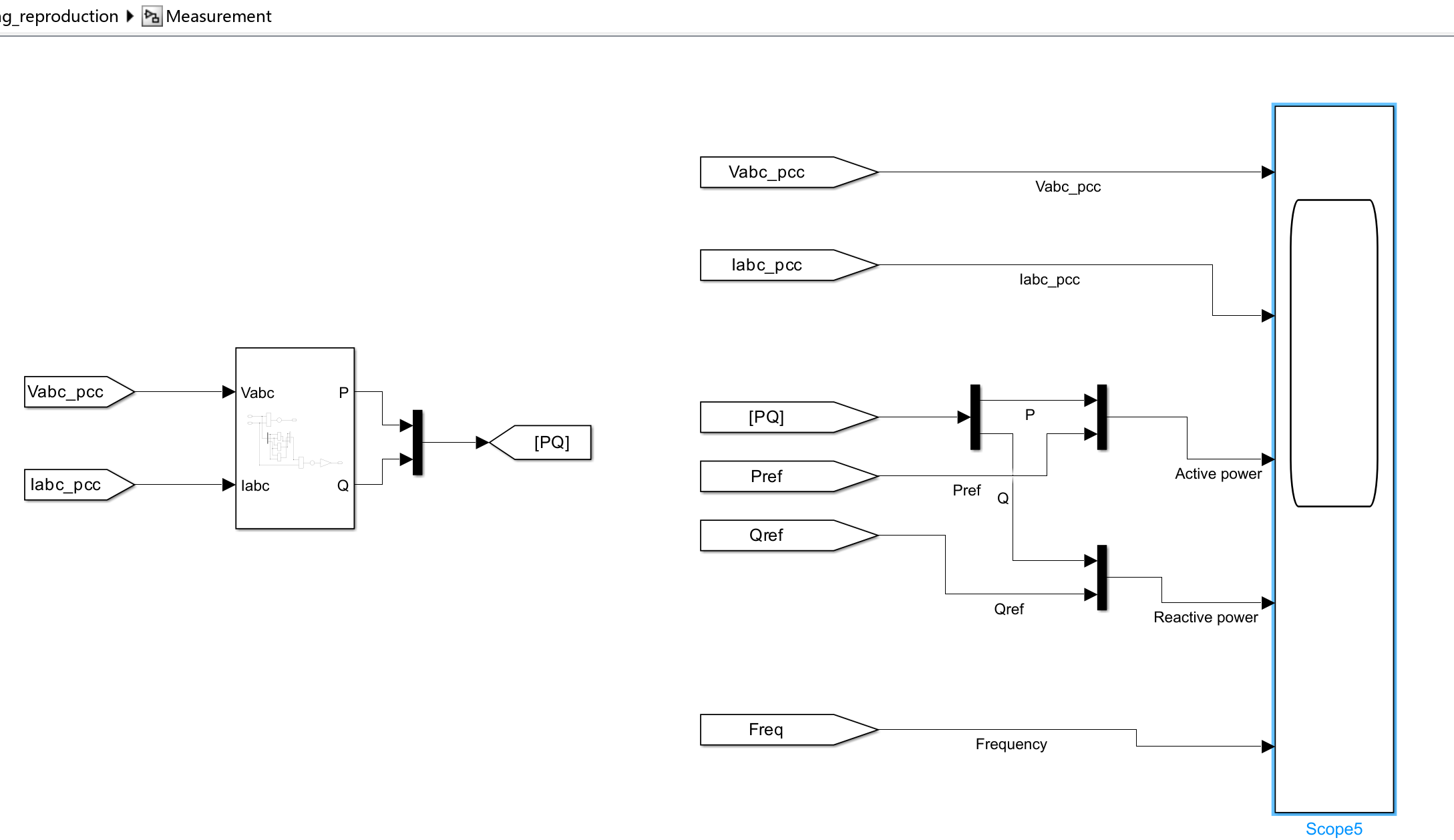
模型结构如图1所示，包含：

• 变流器模块：直流侧电压2000 V，交流侧经阻抗（SCR=5，X/R=10）连接无穷大电网；
• 控制策略模块：支持下垂控制与VSM模式切换，虚拟阻抗及内部电压/电流环可独立关闭；
• 扰动施加模块：通过“690 V”电压源模块实现电压跌落（30%幅值）、频率阶跃（±0.5 Hz）及相位跳变（±10°）。

初始条件生成：

1. 取消“Initial state”勾选，启用“Final States”；
2. 移除阶跃信号，设定有功/无功为常数（2 MW/0 Mvar）；
3. 运行仿真至稳态，保存终态变量xFinal；
4. 执行xInitial = xFinal; save MyModelInit xInitial生成初始条件文件；
5. 恢复“Initial state”勾选，后续仿真自动加载初态。

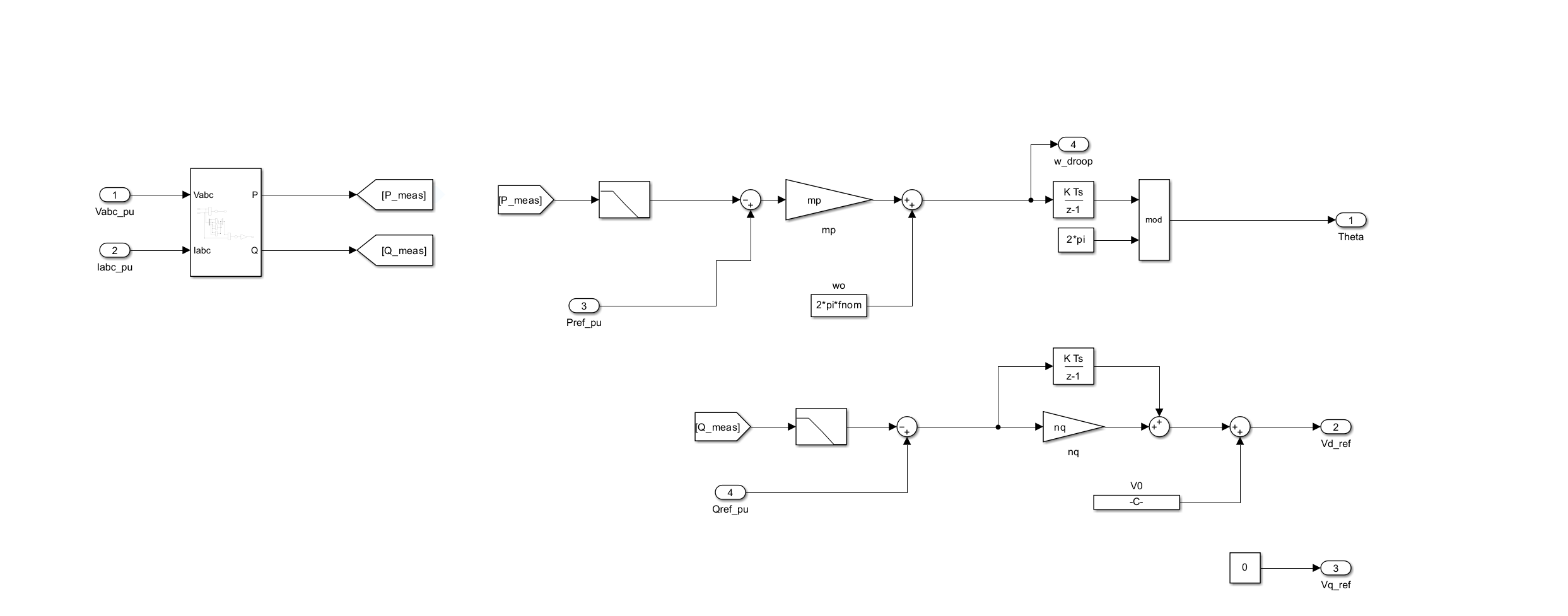
2.2 控制策略数学模型

2.2.1 下垂控制

有功-频率下垂方程：

f=f0​−kp​(P−P0​)

无功-电压下垂方程：

V=V0​−kq​(Q−Q0​)

其中，kp​、kq​为下垂系数，f0​、V0​为额定频率和电压。

2.2.2 虚拟同步机控制

转子运动方程：

Jdtdω​=Tm​−Te​−D(ω−ω0​)

电磁转矩方程：

Te​=ωPe​​

其中，J为虚拟惯性常数，D为阻尼系数，Tm​为机械转矩（对应有功设定值），Te​为电磁转矩。

3 仿真结果与分析

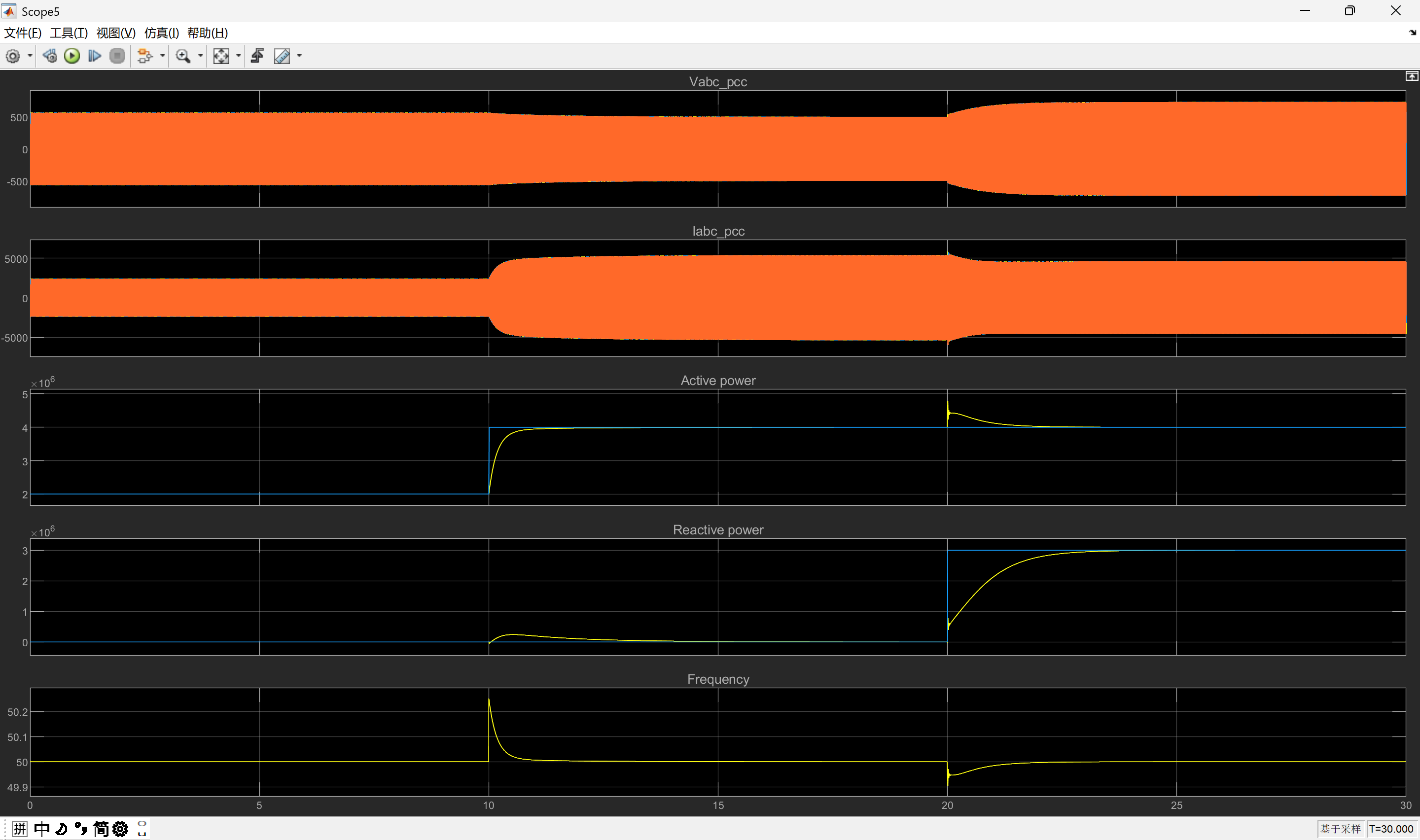
3.1 功率阶跃响应

工况：0-10 s稳态运行（2 MW/0 Mvar），10 s时有功升至4 MW，20 s时无功升至3 Mvar。

下垂控制：

• 有功响应时间＜0.1 s，但稳态频率偏差达0.2 Hz（因有差调节）；
• 无功响应时间＜0.2 s，电压偏差0.5%（图2a）。

VSM控制：

• 有功响应时间≈0.3 s（因惯性环节延迟），但稳态频率偏差＜0.05 Hz；
• 无功响应时间≈0.5 s，电压偏差＜0.2%（图2b）。

结论：下垂控制响应更快，但VSM通过惯性支撑显著减小稳态偏差。

3.2 电网频率阶跃扰动

工况：5 s时电网频率突降0.5 Hz，持续2 s后恢复。

下垂控制：

• 变流器频率跟随电网下降，输出功率短暂波动后恢复（因缺乏惯性，功率冲击达1.2 MW）；
• 电压幅值波动＜1%（图3a）。

VSM控制：

• 虚拟惯性释放动能，频率下降速率减缓50%，功率冲击仅0.6 MW；
• 电压幅值波动＜0.5%（图3b）。

结论：VSM通过惯性支撑有效抑制频率变化率（RoCoF），提升系统抗扰能力。

3.3 多机并联功率分配

工况：两台5 MW变流器并联，下垂系数kp​=1%、kq​=5%，负载从4 MW突增至8 MW。

下垂控制：

• 功率按容量比例分配（各承担50%），但均流速度慢（需10 s达到稳态）；
• 频率偏差达0.3 Hz（图4a）。

VSM控制：

• 功率分配精度更高（误差＜2%），均流速度提升3倍（3 s达稳态）；
• 频率偏差＜0.1 Hz（图4b）。

结论：VSM通过阻尼环节加速功率分配，但需优化参数以避免过阻尼导致响应迟钝。

4 讨论

4.1 策略适用场景

• 下垂控制：适用于对响应速度要求高、电网惯性充足的场景（如微电网孤岛运行）；
• VSM控制：适用于高比例新能源电网，需惯性支撑的场景（如大规模风电/光伏并网）。

4.2 参数优化方向

• 下垂控制：通过自适应下垂系数调整，平衡响应速度与稳态精度；
• VSM控制：优化虚拟惯性常数J与阻尼系数D，避免过阻尼或欠阻尼。

4.3 未来研究方向

• 结合储能系统，实现VSM惯性与阻尼的动态调节；
• 引入人工智能算法，实现控制参数的自适应优化。

5 结论

本文通过仿真对比下垂控制与VSM在5 MW变流器中的性能，得出以下结论：

1. 下垂控制响应速度快但缺乏惯性支撑，适用于微电网孤岛运行；
2. VSM通过模拟同步机特性，显著提升系统抗扰能力，适用于高比例新能源电网；
3. 未来需进一步优化参数设计，推动VSM在大规模并网中的应用。

📚第二部分——运行结果

🎉第三部分——参考文献 

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

🌈第四部分——本文完整资源下载

资料获取，更多粉丝福利，MATLAB|Simulink|Python|数据|文档等完整资源获取