【无人机路径规划】解码四轴飞行器的 “精准舞步”：轨迹跟随仿真大揭秘（Matlab实现）

本文链接：https://blog.youkuaiyun.com/Matlab88888/article/details/149090415

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

在无人机技术飞速发展的今天，四轴飞行器凭借其灵活的机动性和广泛的应用场景，成为大众关注的焦点。无论是高空拍摄绝美风景，还是执行复杂的巡检任务，四轴飞行器都需要按照预定轨迹精准飞行。而四轴飞行器轨迹跟随仿真，就是帮助它们在实际飞行前，模拟出 “精准舞步” 的关键技术，今天就带大家一探究竟。

四轴飞行器：空中舞者的基本原理

四轴飞行器由四个旋翼组成 “X” 或 “+” 字形结构，通过四个旋翼不同的转速组合来实现各种飞行动作。当四个旋翼转速相同，飞行器保持悬停；增加某个旋翼转速，减少对应旋翼转速，就能实现前进、后退、左转、右转等动作。但在空中复杂环境下，要让四轴飞行器严格按照规划的轨迹飞行并非易事，这就需要轨迹跟随仿真技术来保驾护航。

轨迹跟随仿真：飞行前的 “彩排”

四轴飞行器轨迹跟随仿真，就像是飞行前的一场 “彩排”。工程师们在计算机虚拟环境中，搭建四轴飞行器的模型，设定预定飞行轨迹，然后模拟飞行器在各种条件下沿着这条轨迹飞行的过程。通过仿真，可以提前预测飞行器在实际飞行中可能遇到的问题，比如轨迹偏差、姿态不稳定等，进而优化控制算法和飞行参数，确保实际飞行安全又精准。

仿真流程与关键技术

模型搭建

首先要建立四轴飞行器的数学模型，这个模型涵盖了飞行器的动力学和运动学特性。简单来说，就是用数学公式描述飞行器在不同旋翼转速、外界风力等因素影响下，姿态和位置的变化规律。同时，还要构建飞行环境模型，模拟真实的大气环境、地形地貌等，让仿真更贴近实际情况。

轨迹规划

根据任务需求，规划出合理的飞行轨迹。轨迹可以是直线、曲线，也可以是复杂的三维空间路径。例如，在电力巡检任务中，轨迹需要围绕输电线路设计，确保飞行器能全面检查线路状况。规划轨迹时，还要考虑飞行器的性能限制，如最大速度、最大转角等，保证轨迹是飞行器能够实现的。

控制算法设计

控制算法是轨迹跟随仿真的核心。常见的控制算法有 PID 控制、模型预测控制等。这些算法就像飞行器的 “大脑”，根据当前位置与预定轨迹的偏差，实时调整四个旋翼的转速，让飞行器不断修正飞行姿态，跟上预定轨迹。比如，当飞行器偏离轨迹时，控制算法迅速计算出需要增加或减少哪些旋翼的转速，使飞行器回到正确路径上。

仿真与分析

在完成模型搭建、轨迹规划和控制算法设计后，开始进行仿真实验。通过计算机模拟飞行器的飞行过程，记录飞行数据，如位置、速度、姿态角等。工程师们分析这些数据，评估飞行器的轨迹跟随性能，查看是否存在轨迹偏差过大、飞行不稳定等问题。如果发现问题，就对模型、轨迹或控制算法进行优化，然后再次仿真，直到达到满意的效果。

实际应用场景

四轴飞行器轨迹跟随仿真技术在众多领域发挥着重要作用。在农业领域，通过仿真优化轨迹，四轴飞行器可以精准地在农田上方飞行，进行农药喷洒、作物监测等作业，提高效率且减少农药浪费；在物流配送中，仿真能帮助规划安全、高效的配送路线，让四轴飞行器准确地将货物送达指定地点；在影视拍摄方面，仿真确保飞行器沿着最佳拍摄轨迹飞行，拍出稳定、流畅的画面，助力导演实现创意构想。

未来展望

随着计算机技术、传感器技术和控制理论的不断发展，四轴飞行器轨迹跟随仿真技术也将持续升级。未来，仿真可能会更加逼真，能够模拟更复杂的环境因素和突发状况；控制算法将更加智能，实现更精准的轨迹跟随；同时，仿真技术还可能与人工智能、物联网等技术深度融合，为四轴飞行器开拓更多新的应用场景，让这些空中舞者在未来的舞台上展现出更精彩的 “舞步”。

📚2 运行结果

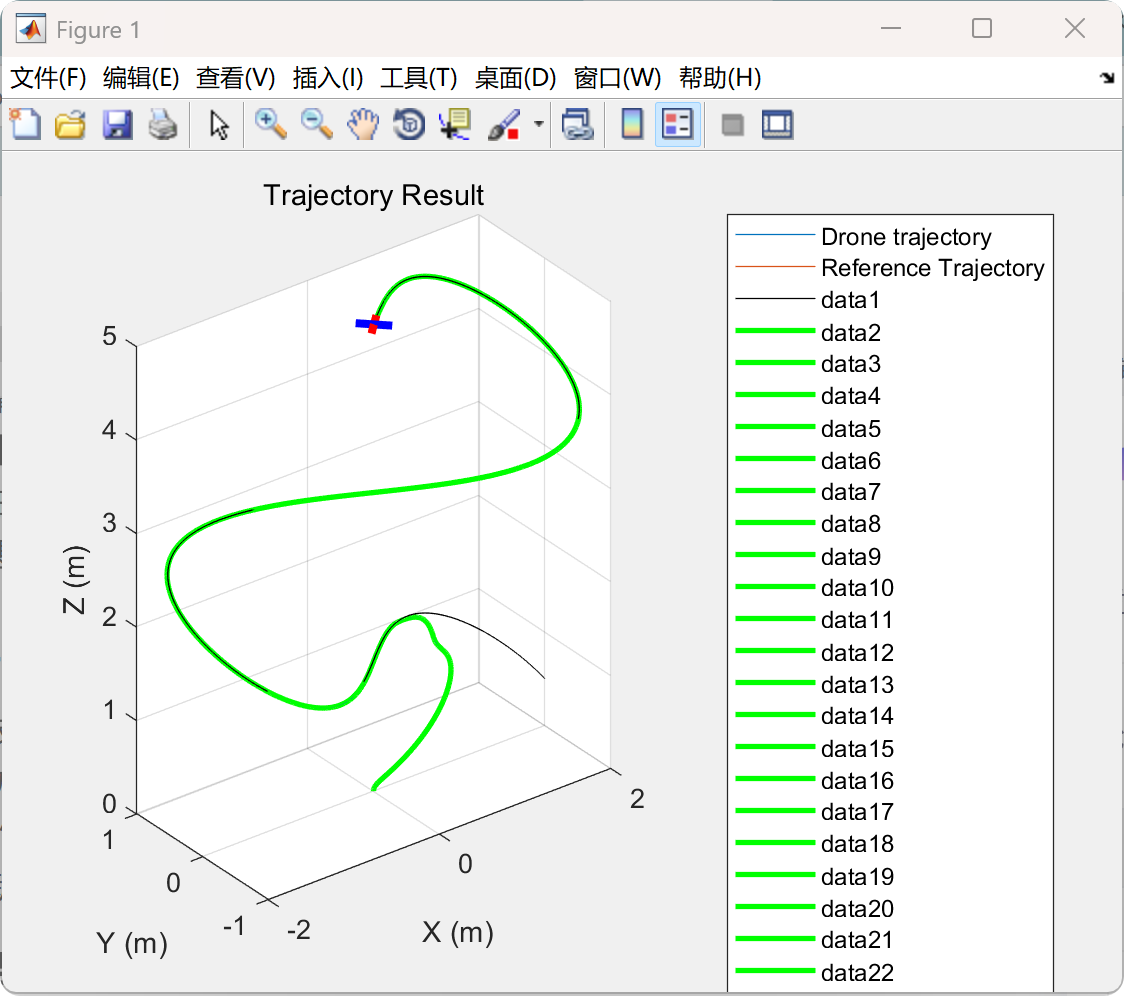
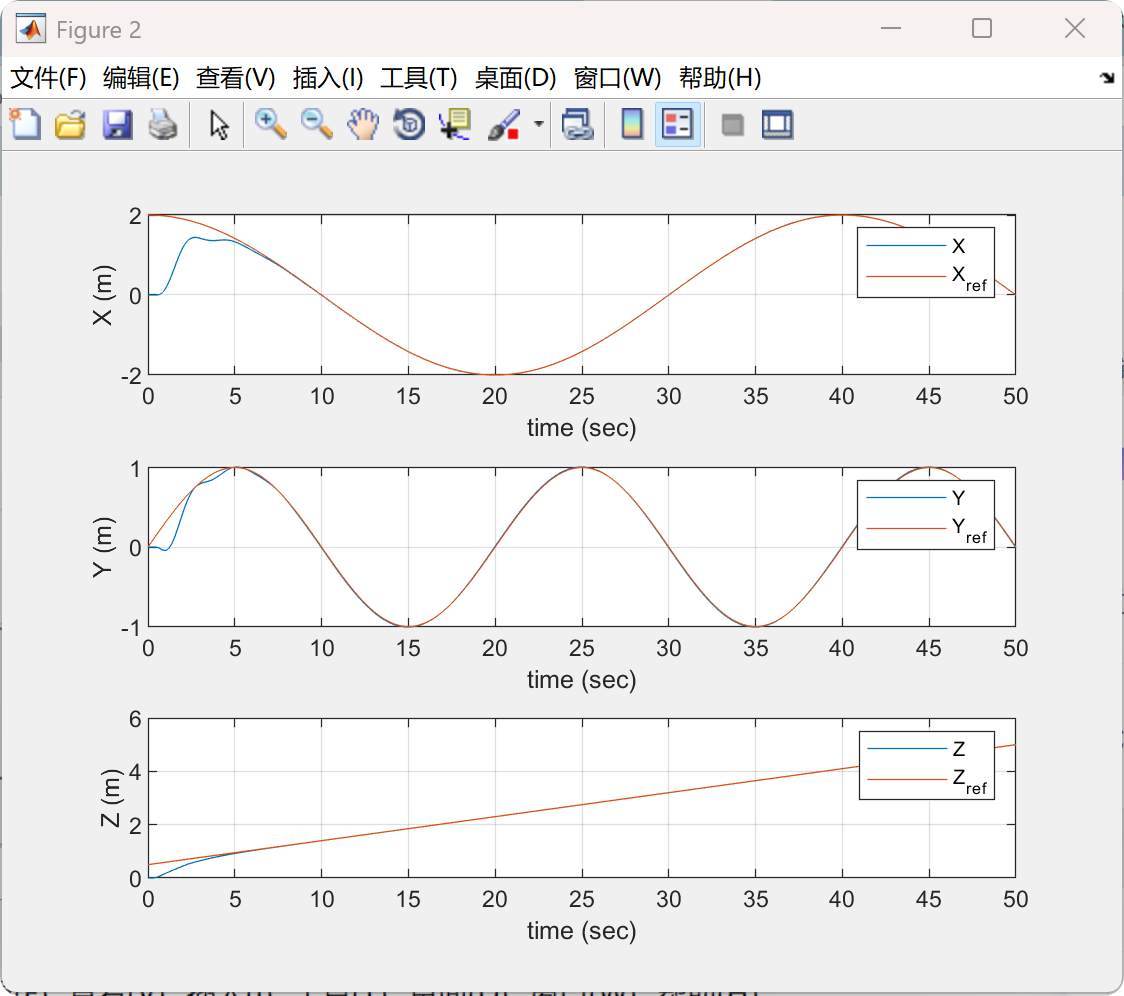
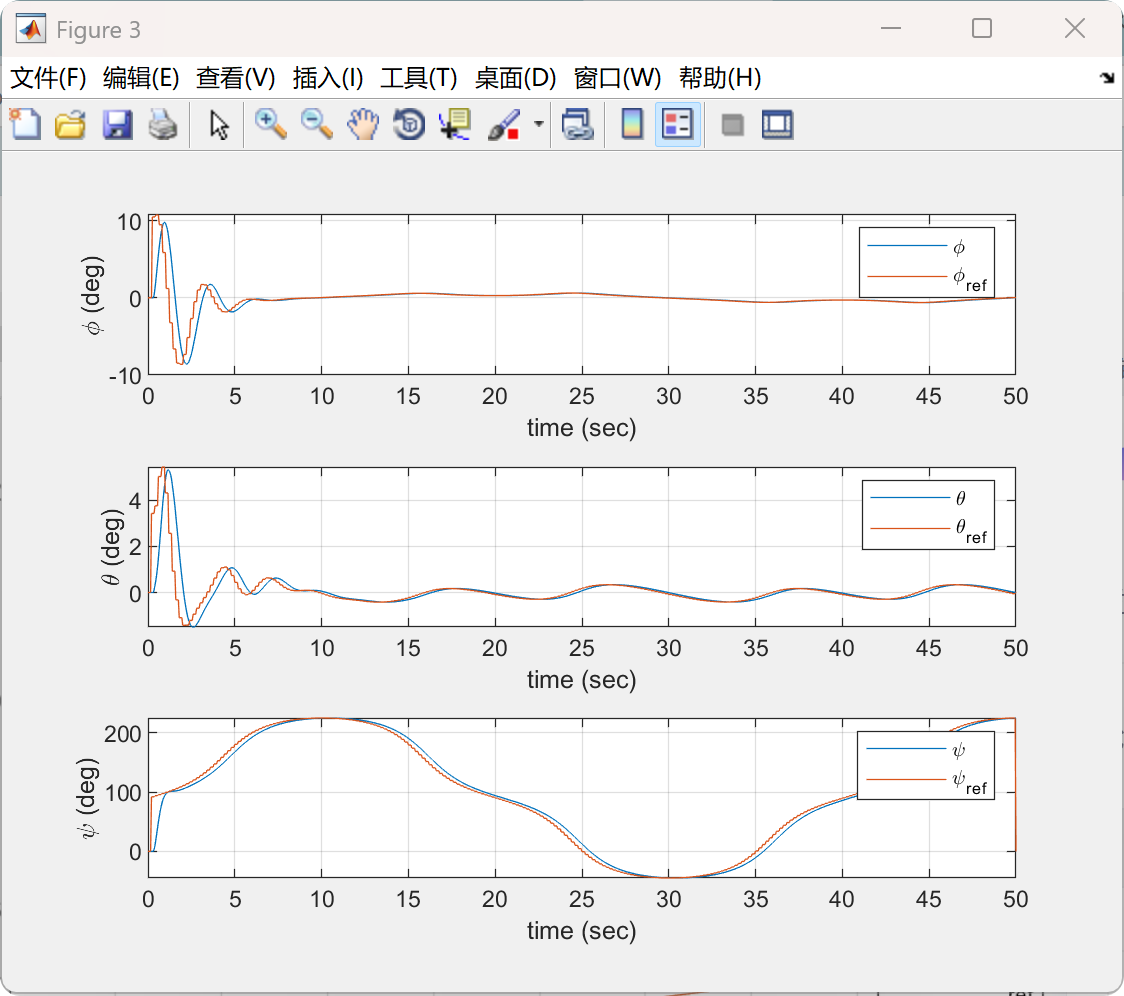
部分代码：

%% Drone Simulation
clear; clc;
%% Time Stamps
t_end = 50;
h = 0.05;
t = 0:h:t_end;
sol = zeros(length(t), 15);

%% Parameters
m = 0.698;
Ixx = 0.0034;
Iyy = 0.0034;
Izz = 0.006;
J = 1.302*10^(-6);
Ct = 7.6184*(10^(-8))*(60/(2*pi))^2;
Ctheta = 2.6839*(10^(-9))*(60/(2*pi))^2;
l = 0.171;
g = 9.81;
%% Initial Conditions
state0 = [0, 0, 0,  0, 0, 0,  0, 0, 0,  0, 0, 0,  0, 0, 0];
sol(1,:) = state0;

U1=m*g; U2=0; U3=0; U4=0; % Initial Inputs

Omega = Inp2Omega(U1, U2, U3, U4, Ct, Ctheta, l);

phi_d = 0;theta_d = 0; psi_d = 0; % Initial Euler Angles

% Initial parameters
params = [m,Ixx,Iyy,Izz,J,Omega,U1,U2,U3,U4,phi_d,theta_d,psi_d];

%% Position Controller gains
[k1x, k2x] = poleplace(-1, -1);
[k1y, k2y] = poleplace(-1, -1);
[k1z, k2z] = poleplace(-1, -1);


%% Record Results
pos = zeros(length(t), 3);
vel = zeros(length(t), 3);
phi_ref = zeros(length(t), 1);
theta_ref = zeros(length(t), 1);

%% Reference Trajectory
[Xr,Yr,Zr,Xdr,Ydr,Zdr,Xddr,Yddr,Zddr, psi_ref] = refTraj3(t);

%% Solver
j = 0;
for i = 1:length(t)-1
    % Using Runge Kutta to propagate
    sol(i+1,:) = RK8(@diffEqn, t(i), sol(i, :), h, params);

    % Unpack integrated states
    % Euler Angles
    phi = sol(i+1, 1);

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]李白杨,祝小平,周洲,等.基于螺旋桨壁面效应的四旋翼无人机超机动栖息研究[J/OL].兵工学报,1-12[2025-07-03].http://kns.cnki.net/kcms/detail/11.2176.TJ.20250702.1208.004.html.

[2]陈欣淼,郑柏超,翟忠浩.受故障影响的四旋翼无人机编队滑模容错控制[J/OL].飞行力学,1-8[2025-07-03].https://doi.org/10.13645/j.cnki.f.d.20250630.001.