【路径规划】使用 Genetic Algorithm 解决机器人路径规划问题（Matlab实现）-优快云博客

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

使用遗传算法解决机器人路径规划问题在机器人领域，路径规划是一项关键任务，旨在为机器人找到从起始位置到目标位置的最优或接近最优路径。遗传算法作为一种强大的优化算法，在解决机器人路径规划问题上具有显著优势。遗传算法通过模拟自然进化过程来搜索最优解。在机器人路径规划中，首先需要将路径问题进行编码，通常可以将路径表示为一系列的坐标点或者特定的数据结构。然后，初始化一个包含多个潜在路径的种群。适应度函数在遗传算法中起着核心作用。对于机器人路径规划，适应度函数可以根据路径的长度、安全性、平滑度等因素来评估每个路径的优劣。路径越短、避开障碍物的能力越强、运动越平滑，其适应度就越高。通过遗传操作，如选择、交叉和变异，不断地改进种群中的路径。选择操作根据适应度挑选出较优的路径作为父代，交叉操作将父代路径进行组合以产生新的路径，变异操作则对路径进行随机的改变，增加种群的多样性。随着迭代的进行，种群中的路径逐渐优化，最终收敛到一个较好的解决方案，即机器人的最优或接近最优路径。遗传算法能够处理复杂的环境，包括存在多个障碍物、动态变化的环境等情况，为机器人在不同场景下的路径规划提供了一种有效的方法。

📚2 运行结果

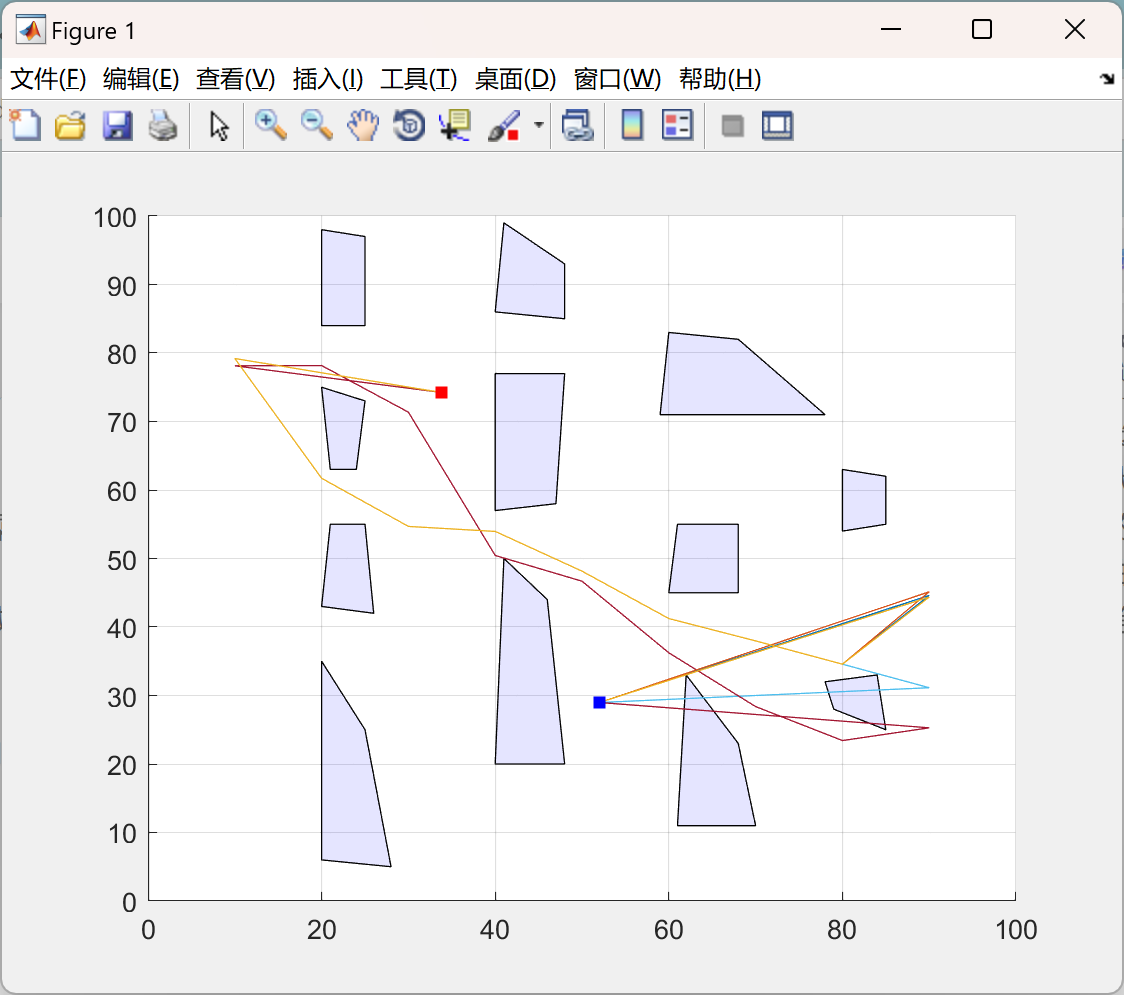
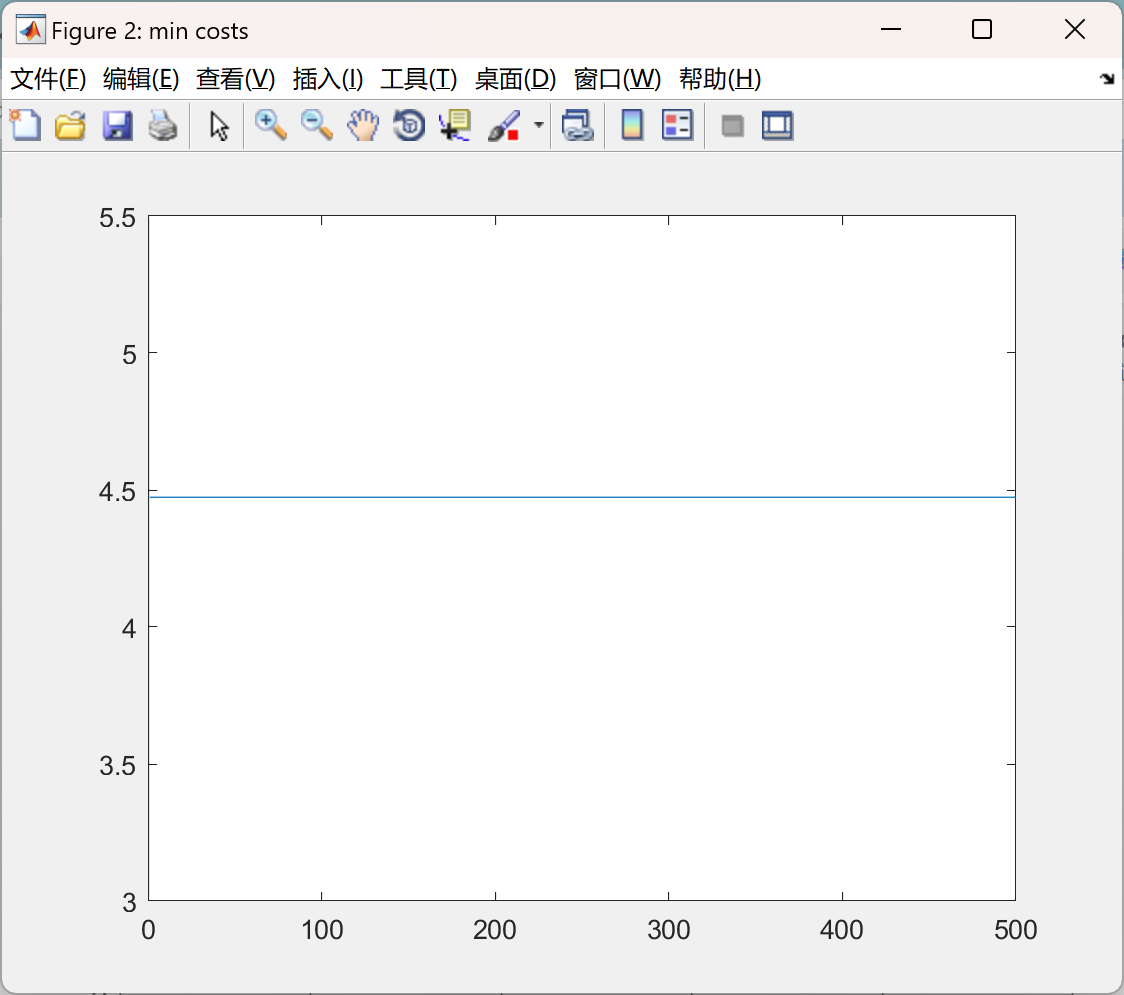
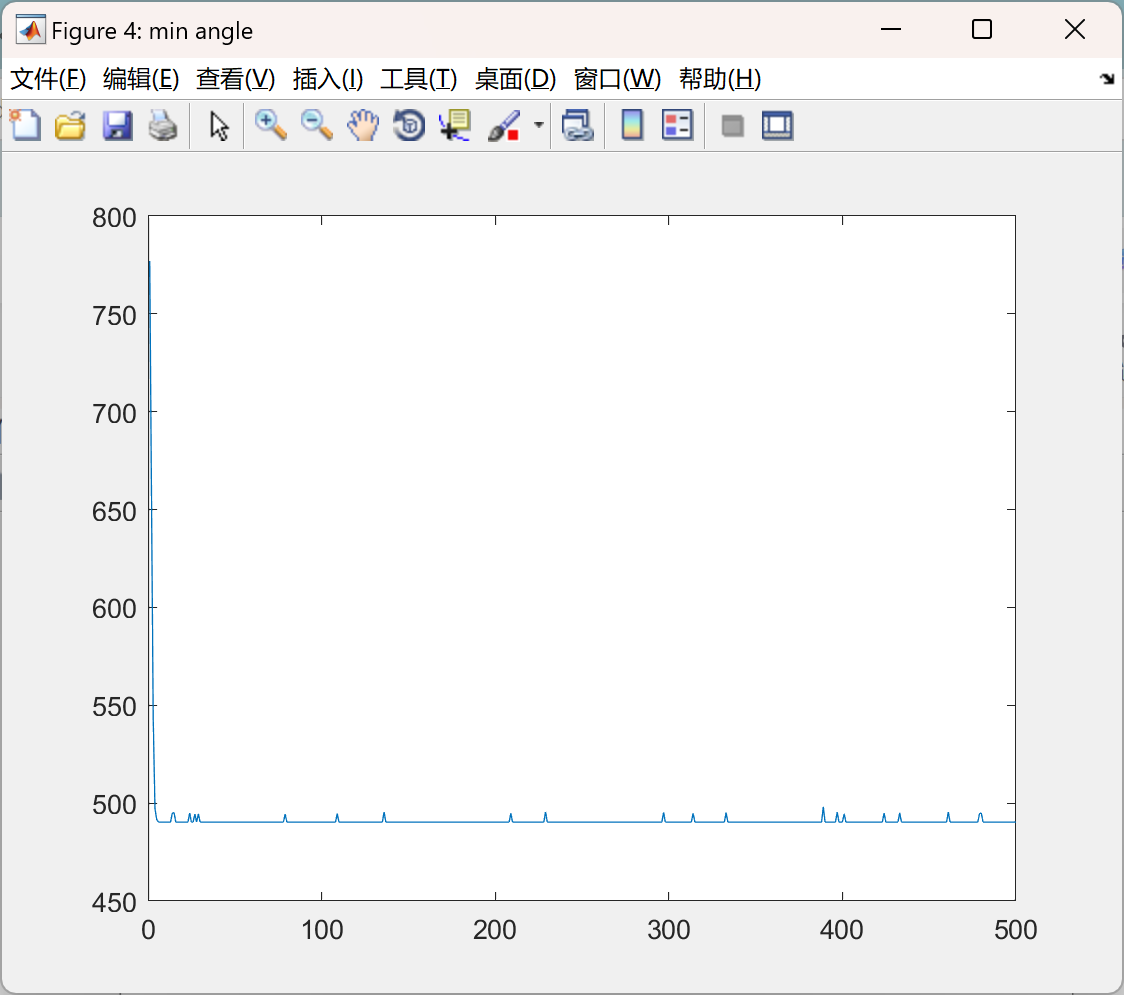
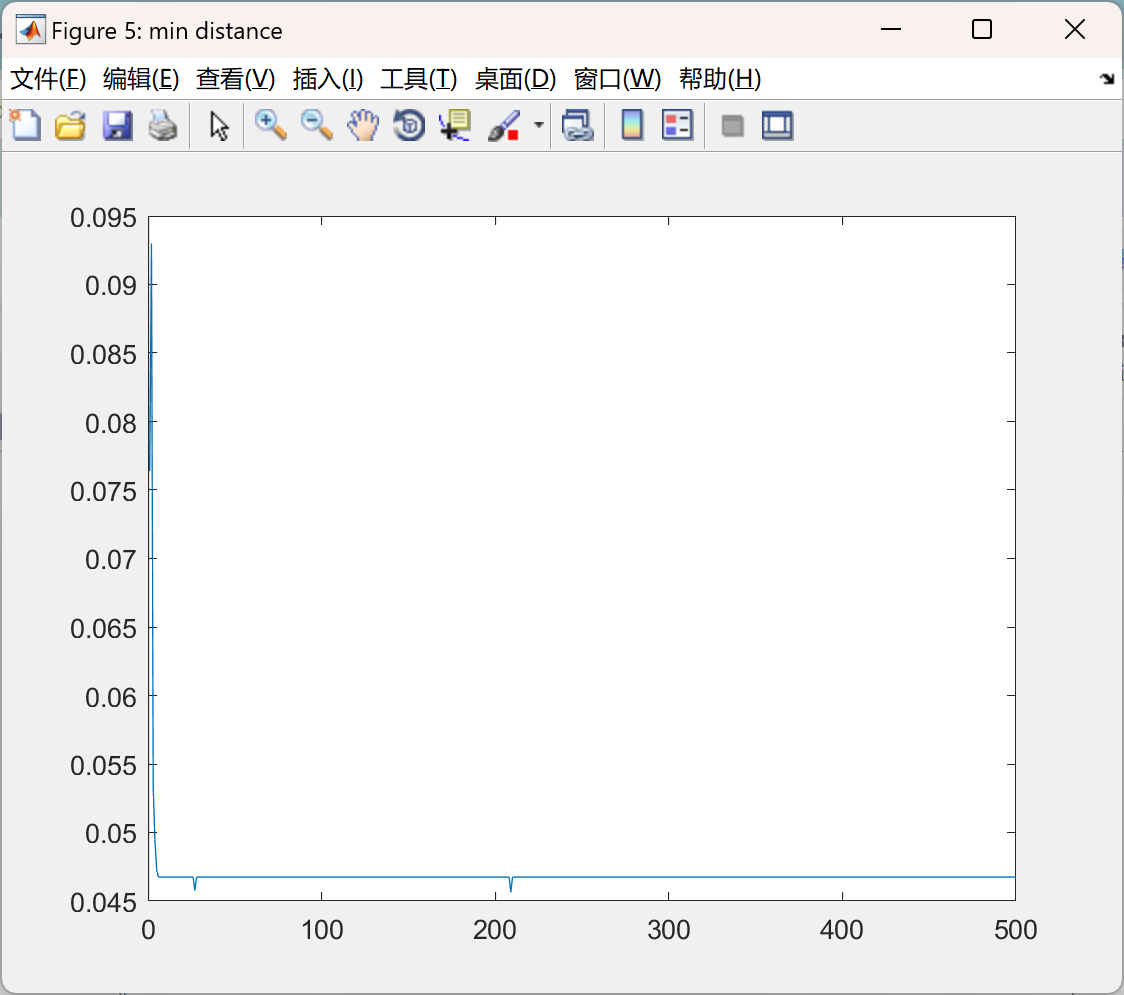
主函数部分代码：


clear all;
close all;
clc;

%% Create and plot Obstacle

areax = 100;
areay = 100;
% Obstacle Locations
O_loc = [[[20 25 25 20]; [98 97 84 84]]; ...
         [[20 25 24 21]; [75 73 63 63]]; ...
         [[21 25 26 20]; [55 55 42 43]]; ...
         [[20 25 28 20]; [35 25 5 6]];   ...
         [[41 48 48 40]; [99 93 85 86]]; ...
         [[40 48 47 40]; [77 77 58 57]]; ...
         [[41 46 48 40]; [50 44 20 20]]; ...
         [[60 68 78 59]; [83 82 71 71]]; ...
         [[61 68 68 60]; [55 55 45 45]]; ...
         [[62 68 70 61]; [33 23 11 11]]; ...
         [[80 85 85 80]; [63 62 55 54]]; ...
         [[78 84 85 79]; [32 33 25 28]]; ...
         ];
swap = size(O_loc);
O_num = swap(1)/2;  %Number of obstacle

% Create obstacles
for i=1:O_num
    n = i*2;
    pgon(i) = polyshape(O_loc(n-1,:),O_loc(n,:));
end
% Plot obstacle
plot(pgon,'FaceColor','blue','FaceAlpha',0.1)
xlim([0,100]);
ylim([0,100]);
hold on
grid on

%% Insert begining and end point

disp('Please,');
disp('select bigining point and then select end point.')
% Ask user for input begining and end point
swap = getline();
beginP = swap(1,:);
endP = swap(2,:);
% Plot begin and end point
scatter(beginP(1), beginP(2),40, 'red', 'filled','s');
scatter(endP(1), endP(2),40, 'blue', 'filled','s');
min_dis = Path_length([beginP; endP]);
disp("minimum distance is: " + min_dis);
disp(".");
disp("..");
disp("...");
%% Initialize population
pop_num = 50;
init_num = 25;
famous = 100*ones(pop_num/5,12);

y_best = (endP(2)-beginP(2))/9*(1:9) + beginP(2);

pop = zeros(init_num,9);
for i=1:9
    pop(:,i) = random('Normal',y_best(i), 8, init_num,1);

end
begin_mat = repmat(beginP(2),init_num,1);
end_mat = repmat(endP(2),init_num,1);
pop = [begin_mat pop end_mat];
x_val = [beginP(1) 10:10:90 endP(1)];
check_flag = 0;
tic;
for j=1:init_num
    k=2;
    while k <= 9
        i=0;
        while i < O_num
            i = i+1;
            while Collision_detect(pgon(i),[x_val(1:k+1); pop(j,1:k+1)])
                pop(j,k:k+1) = random('Normal',(y_best(k)+y_best(k))/2 , 8, 1, 2);
                check_flag = 1;
            end      
            if check_flag == 1
                i = 0;
                check_flag = 0;
            end
        end
        k = k+1;
    end
%     plot(x_val, pop(j,:));
end
disp(toc + " Second primary papulation generating taked!!")
% pop = [pop; zeros(pop_num-init_num,9)];
swap = CrossOver(pop, pop_num-init_num);
swap = Rm_wr_child(pgon, x_val, swap);
disp("primary population cost values");
costs = Cost_func(O_loc, pop, x_val);
pop = [pop; swap];
Draw_path(pgon, x_val, pop);
%% Main Loop (Cost Assignment, Selection, Cross Over and Mutation)
cnt = 0;
it_num = 500;
results = zeros(it_num, 4);
for i=1:it_num
    disp("Iteration " + i + "  ====================>");
    [costs,results(i,2), results(i,3), results(i,4)] = Cost_func(O_loc, pop, x_val);
    rank = Sort_Costs(costs);
    results(i,1) = costs(rank(1));
    disp("Minimum error " + costs(rank(1)));
    famous = Hall_of_fame(pop, costs, rank, famous);
    pop = Path_Selection(rank, pop, init_num);
    swap = CrossOver(pop, pop_num-init_num);
    swap = Mutation(swap,cnt);
    swap = Rm_wr_child(pgon, x_val, swap);
    pop = [pop; swap];
%     size(pop,1)
    cnt = cnt+1;
end