【数据驱动】【基于分布的 Hilbert 空间嵌入的随机最优控制】提出一种方法来计算具有任意干扰的随机系统的近似最优策略（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据、文章

---

💥1 概述

文献来源：

摘要：
分布的核嵌入最近在机器学习领域引起了广泛关注，作为一种表示概率分布的数据驱动技术。广义上，这些技术通过将积分算子表示为再生核 Hilbert 空间中的元素，实现了期望的高效计算。我们将这些技术应用于随机最优控制理论领域，并提出一种方法来计算具有任意干扰的随机系统的近似最优策略。我们的方法将优化问题简化为一个线性规划问题，可以通过拉格朗日对偶轻松求解，而无需求助于基于梯度的优化算法。我们专注于离散时间动态规划，并在线性调节问题和非线性目标跟踪问题上展示我们提出的方法。这种方法广泛适用于各种最优控制问题，并提供了一种在数据驱动环境中处理随机系统的方法。

随机系统是无处不在的，然而大多数用于控制随机系统的方法依赖于准确建模系统的动态以及随机过程。随着自主系统变得普遍，并且人类与自主性的直接互动变得更加普遍，对线性和高斯随机性的假设变得值得怀疑，因为它们可能导致令人困惑、非直观或者简单不正确的控制解决方案。当不确定性受到已知值限制时运作良好的强健解可能过于保守，无法应对长尾现象。相比之下，基于数据驱动的方法不依赖于系统动态或随机性的任何先前假设。最近，数据驱动方法引起了相当大的关注，因为学习算法具备处理具有非线性动态和未知干扰的系统的能力。

我们提出了一种基于条件分布嵌入的数据驱动控制器综合方法，这是一种非参数学习技术，利用系统观测样本构建随机系统动态模型，作为再生核 Hilbert 空间中的一个元素。这些技术利用了函数分析和统计学习理论来根据数据经验估计随机核。作为一种非参数技术，核方法是固有的数据驱动方式，不依赖于对数据的先前设定或系统结构的利用。这些技术已被应用于马尔可夫模型、部分可观测系统，以及最近的鲁棒优化方法。此外，这些技术允许有限样本范围，表明随着样本数量趋于无穷，收敛概率为一。Hilbert 空间框架特别适用于随机最优控制问题，主要是因为 Hilbert 空间是内积空间向无限维度的推广，意味着它包含许多感兴趣的优化问题。

文献中对于使用核方法进行策略综合的动机很充分，特别是在强化学习领域。已经开发了通过在再生核 Hilbert 空间中进行功能梯度下降来优化策略的方法。其他方法依赖于值迭代，通过近似值函数作为中间步骤来计算最优控制输入。然而，大多数这些方法面临着重要的计算挑战，因为强化学习使用的采样方案，需要知识的梯度，或依赖于迭代数值方法。已经开始着手解决这些问题，例如使用随机因式分解。

📚2 运行结果

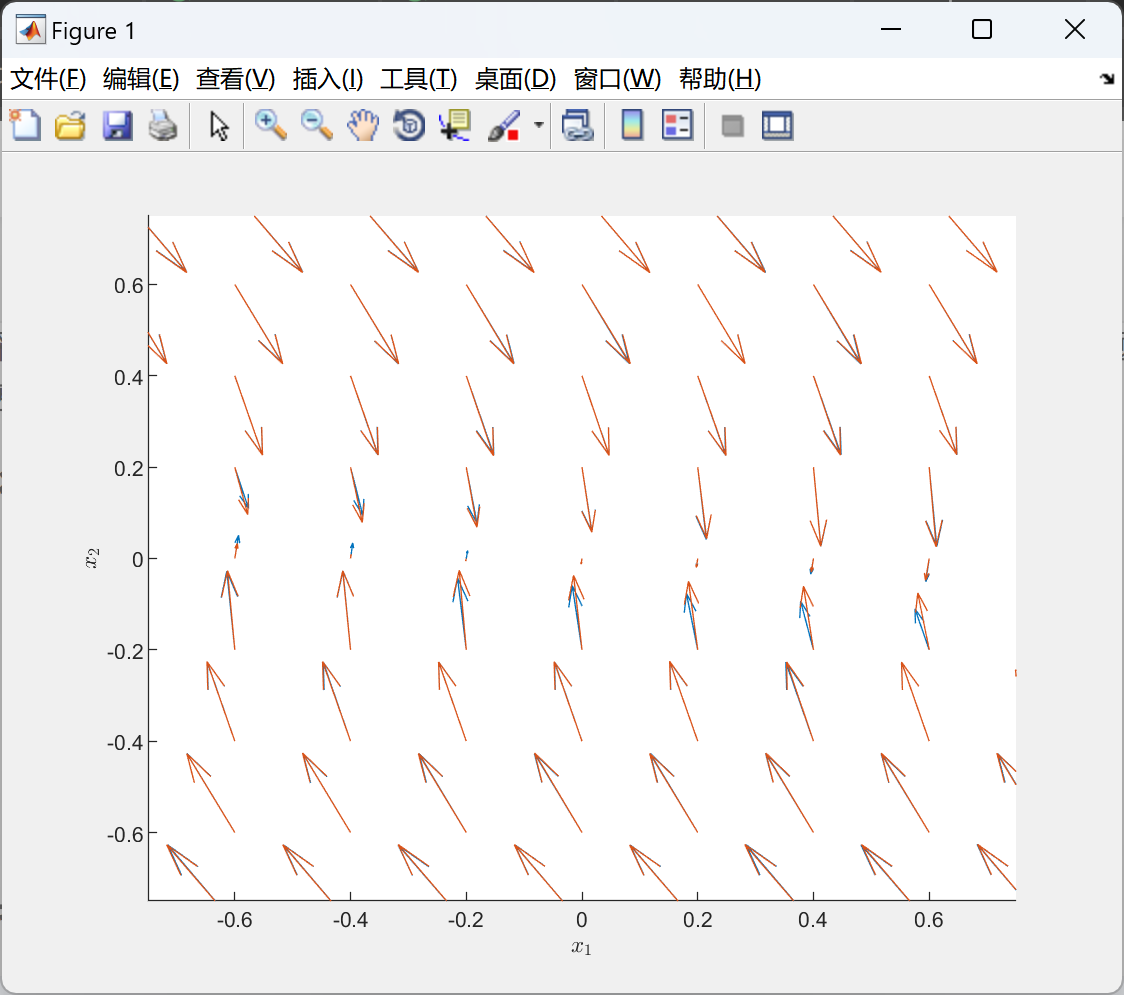
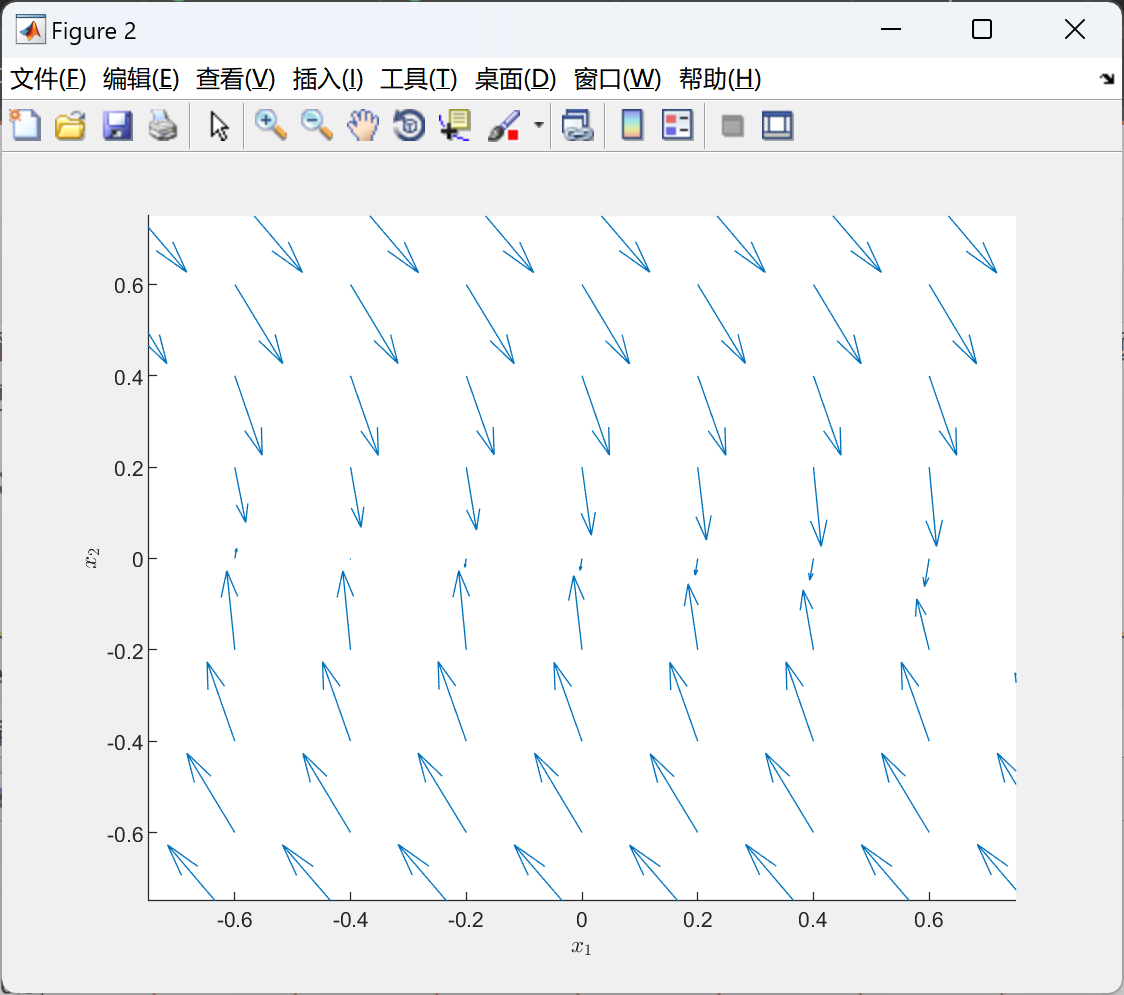
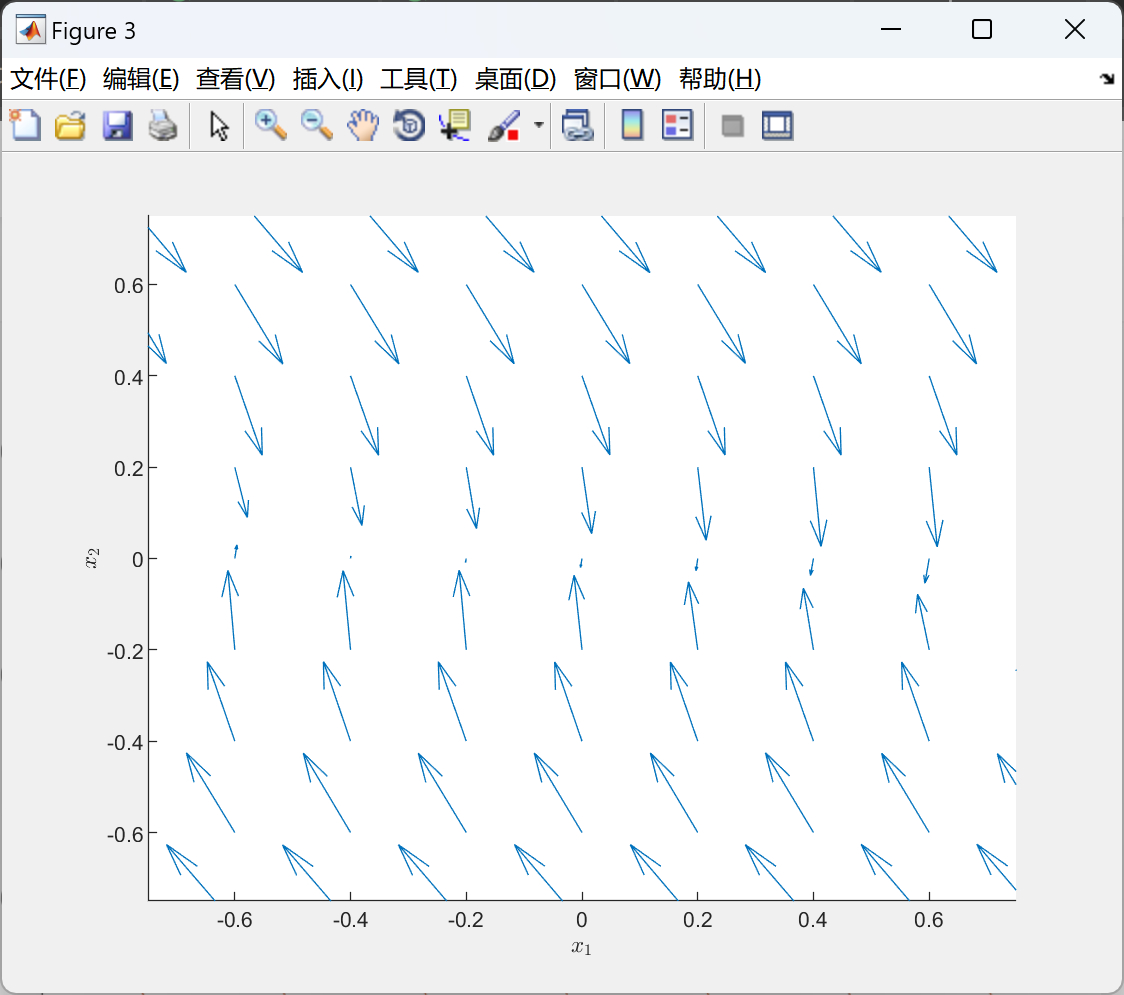
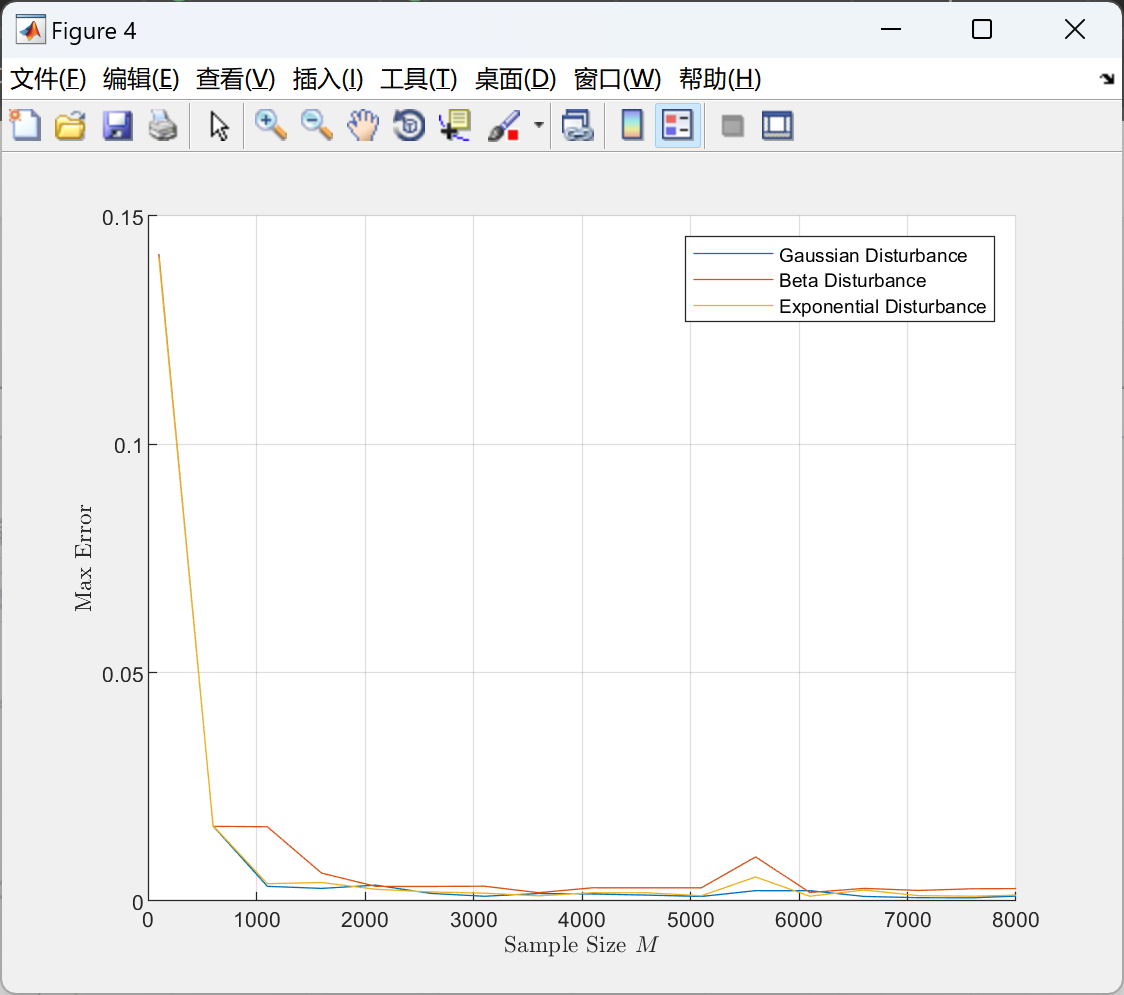
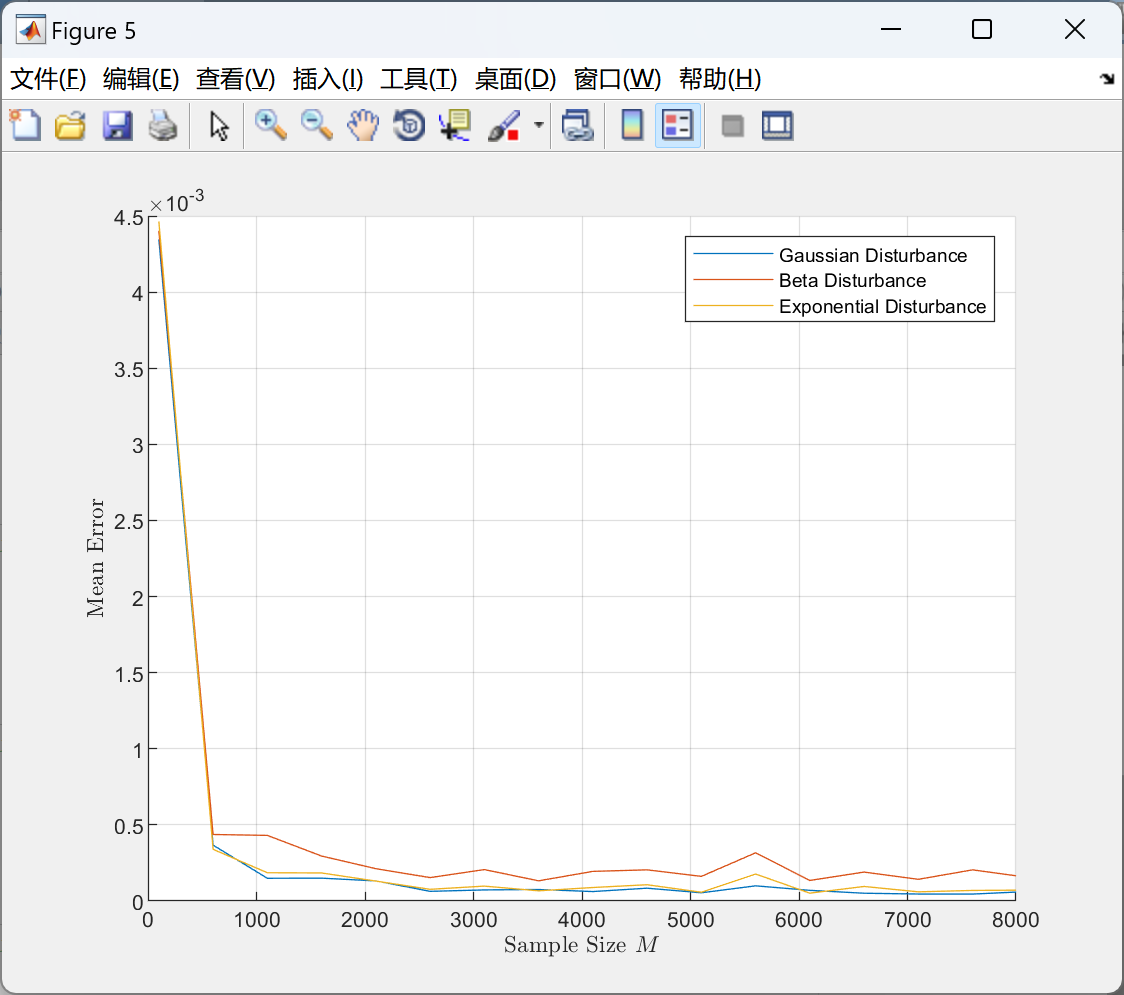
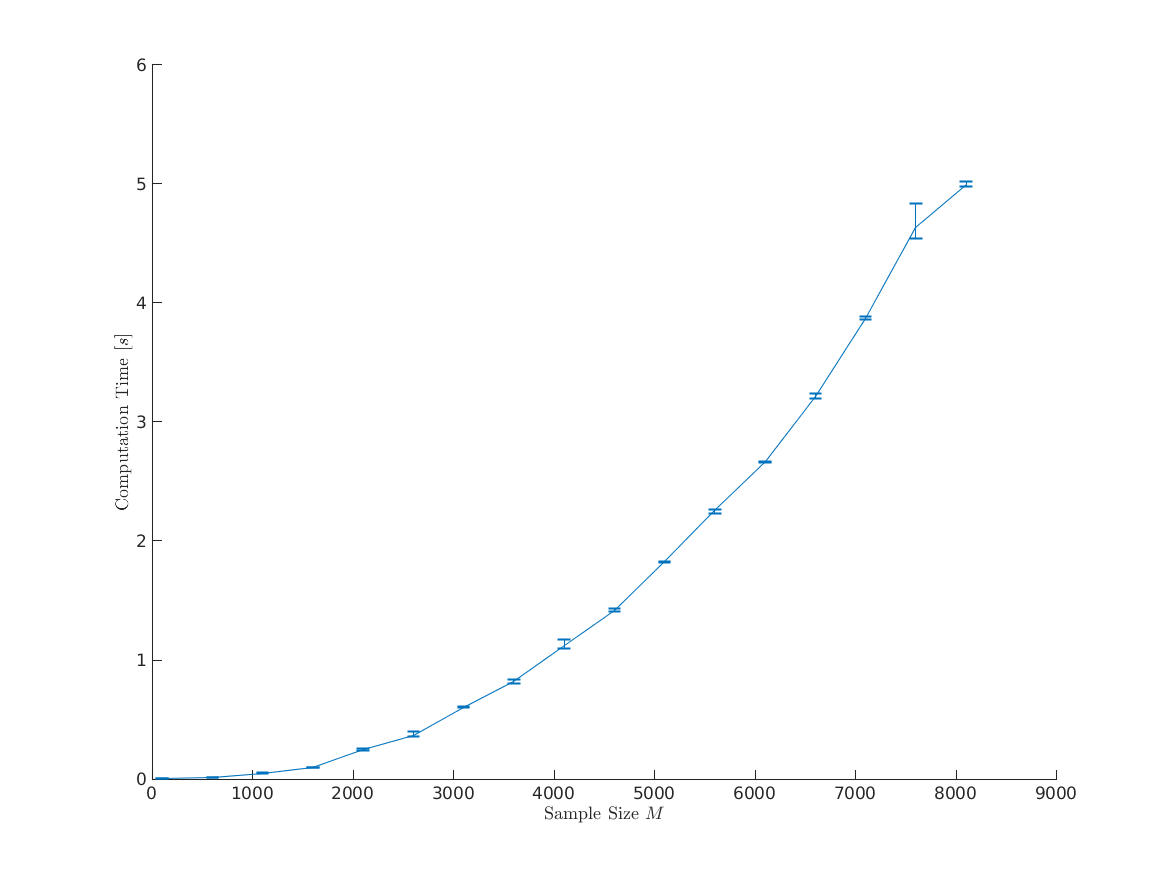
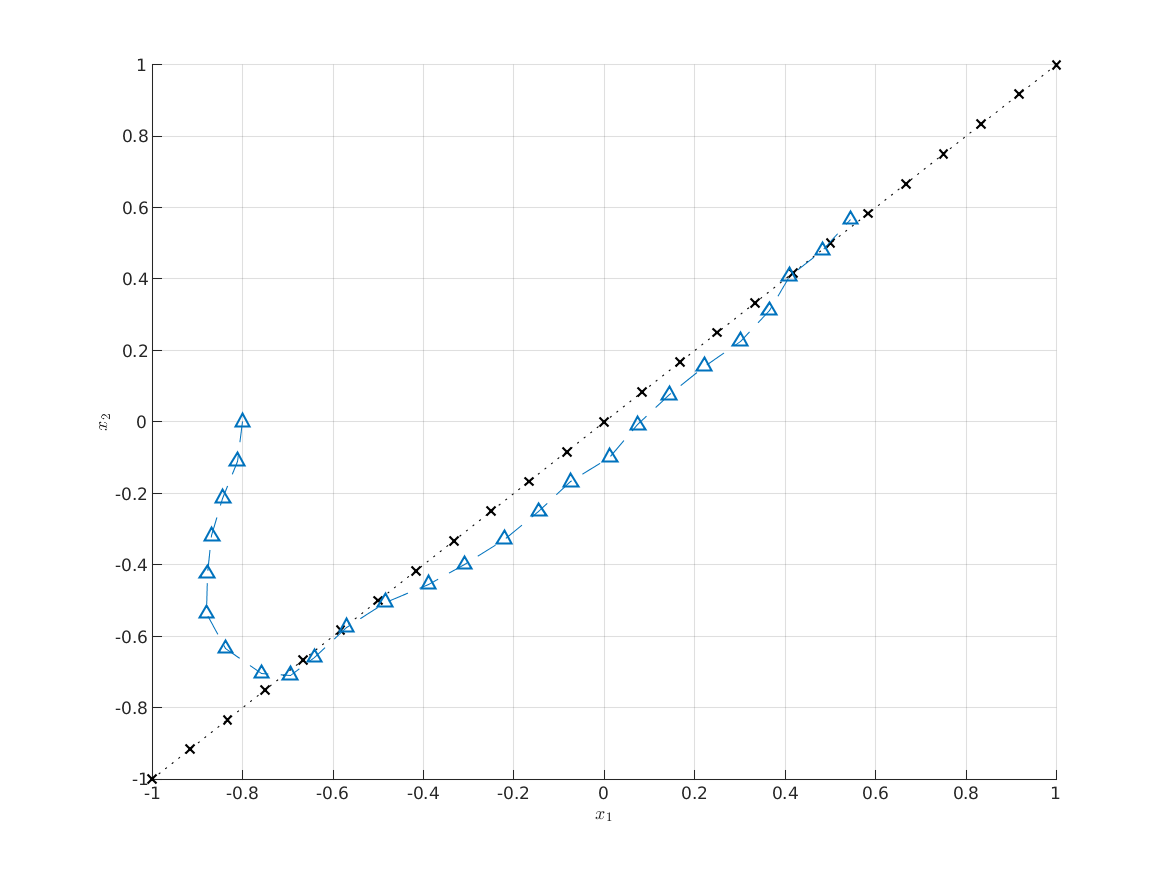
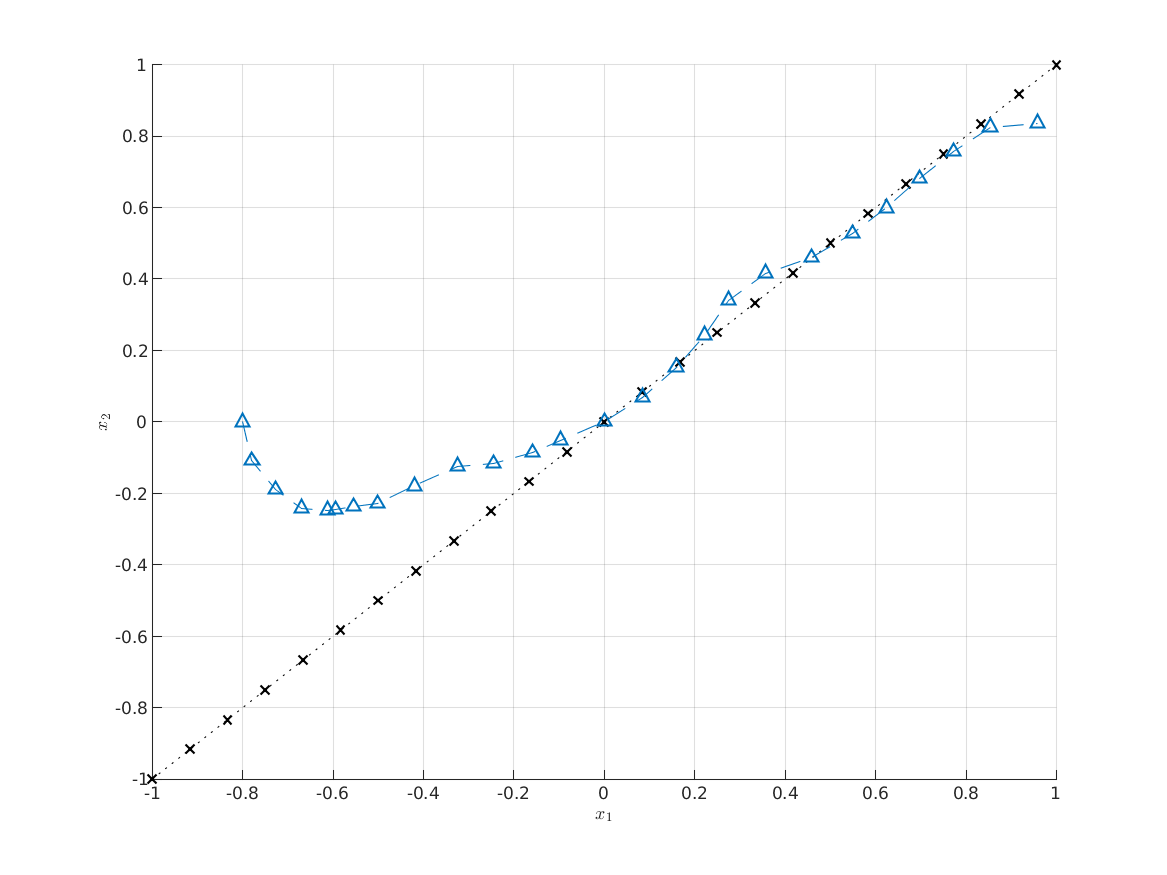 部分代码：

%% Generate Nonholonomic vehicle sample.
% In this file, we generate a sample of observations taken from a system
% with double integrator dynamics. 
% 
% Note that this file is not run during a reproducible run. In order to
% re-generate the sample, this file must be run manually.
% 

rng(0);

%% Define constants.

% Sampling time.
Ts = 0.25;

% Sample size.
M = 1600;

%% Generate the sample. 

xs = [
    -1 + 2*rand(1, M);
    -1 + 2*rand(1, M)
    ];

us = -1.1 + 2.2*rand(1, size(xs, 2));

% % System matrices (double integrator).
% A = [1 Ts; 0 1];
% B = [(Ts^2)/2; Ts];
% 
% % Compute the disturbance.
% W = 0.01*randn(size(xs));
% 
% % Propagate the dynamics forward.
% ys = A*xs + B*us + W;

% Propagate the dynamics forward.
ys = zeros(size(xs));

for p = 1:size(xs, 2)
    ys(:, p) = dynamics_di(xs(:, p), us(:, p), Ts);
end

%% Plot the sample. For debugging.
% Plot the samples under each control input. "Hair" plot.
figure
ax = axes; ax.NextPlot = 'add';
scatter(xs(1, :), xs(2, :))
scatter(ys(1, :), ys(2, :))
for p = 1:size(xs, 2)
    plot([xs(1, p), ys(1, p)], [xs(2, p), ys(2, p)], 'k');
end

%% Save the sample.
% We save the sample to a file in order to reuse the sample across multiple
% experiments. 

save('../data/sample_di.mat', 'Ts', 'M', 'xs', 'us', 'ys');

%% Generate a sample with a Beta disturbance.

% Propagate the dynamics forward.
ys = zeros(size(xs));

for p = 1:size(xs, 2)
    ys(:, p) = dynamics_di_beta(xs(:, p), us(:, p), Ts);
end

%% Save the sample.

save('sample_di_beta.mat', 'Ts', 'M', 'xs', 'us', 'ys');

%% Generate a sample with an Exponential disturbance.

% Propagate the dynamics forward.
ys = zeros(size(xs));

for p = 1:size(xs, 2)
    ys(:, p) = dynamics_di_exp(xs(:, p), us(:, p), Ts);
end

%% Save the sample.

save('sample_di_exp.mat', 'Ts', 'M', 'xs', 'us', 'ys');
 

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

🌈4 Matlab代码、数据、文章