一种用于高斯信号的贝叶斯步进最小均方LMS算法（Matlab代码实现）-优快云博客

本文链接：https://blog.youkuaiyun.com/Matlab88888/article/details/135971344

本文探讨了在LMS算法中通过估计系数和测量噪声的PDF来优化步长的方法，将LMS与卡尔曼滤波器相联系，并利用高斯假设进行概率分析，最终提出基于小卡尔曼滤波器的步长确定算法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

LMS算法在一些条件下，通过使用变化的步长，可以证明等价于卡尔曼滤波器。只要仔细选择卡尔曼滤波器的状态噪声和LMS算法的步长大小。卡尔曼滤波器是在给定状态和测量噪声协方差矩阵的情况下的最佳线性估计器（贝叶斯），但这些矩阵并不总是已知的。本文考虑了这些矩阵未知的情况，特别是当卡尔曼滤波器简化为LMS的特殊情况。这导致了一种算法，可以在几个先验条件下选择LMS算法的步长大小。最佳步长大小可以使用系数估计（qw）和测量噪声方差（qv）的概率密度函数（PDF）的估计来计算。这些概率密度函数可以使用贝叶斯定理和假设高斯参考和测量噪声信号来估计。在进行一些近似之后，得到的算法来确定qw和qv的结果是第二个小型卡尔曼滤波器。

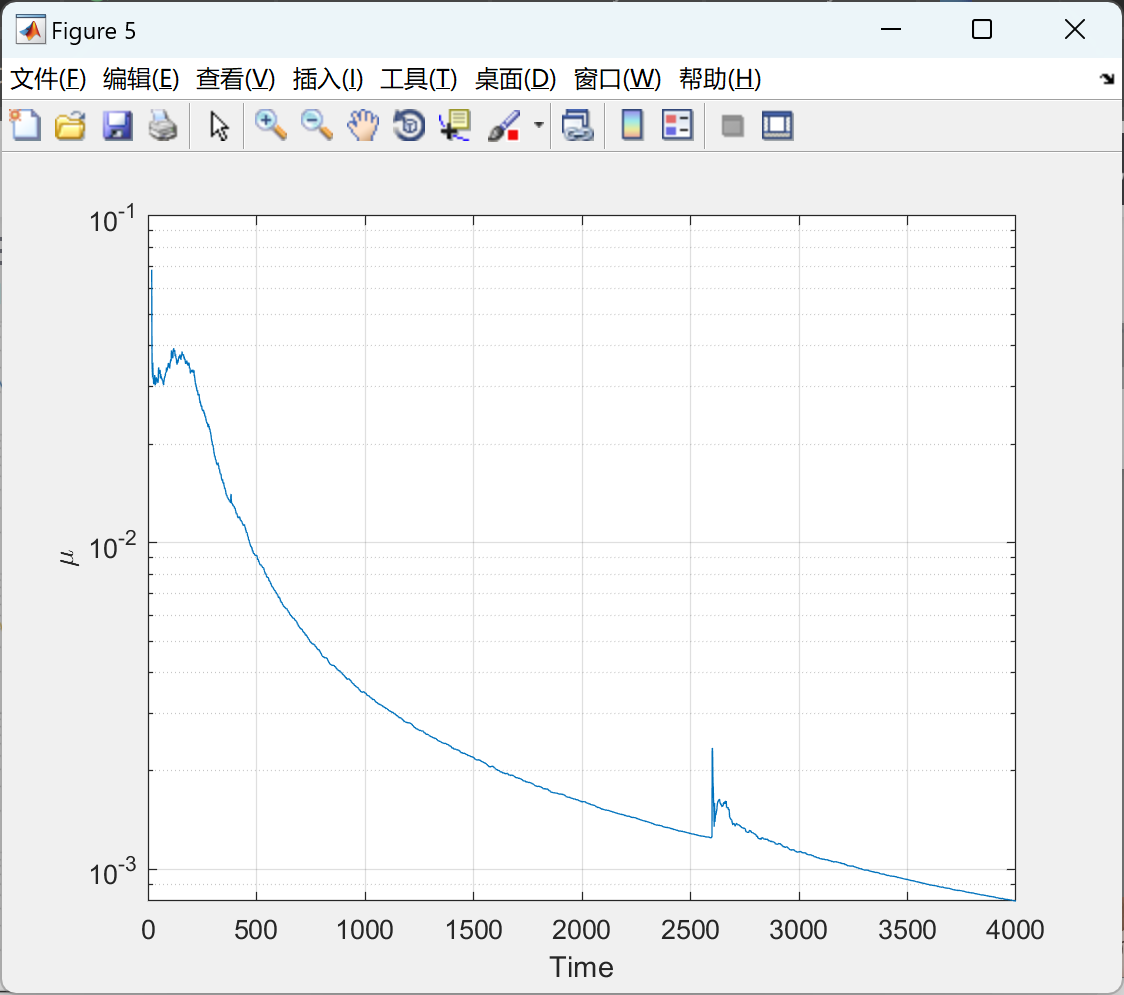
📚2 运行结果

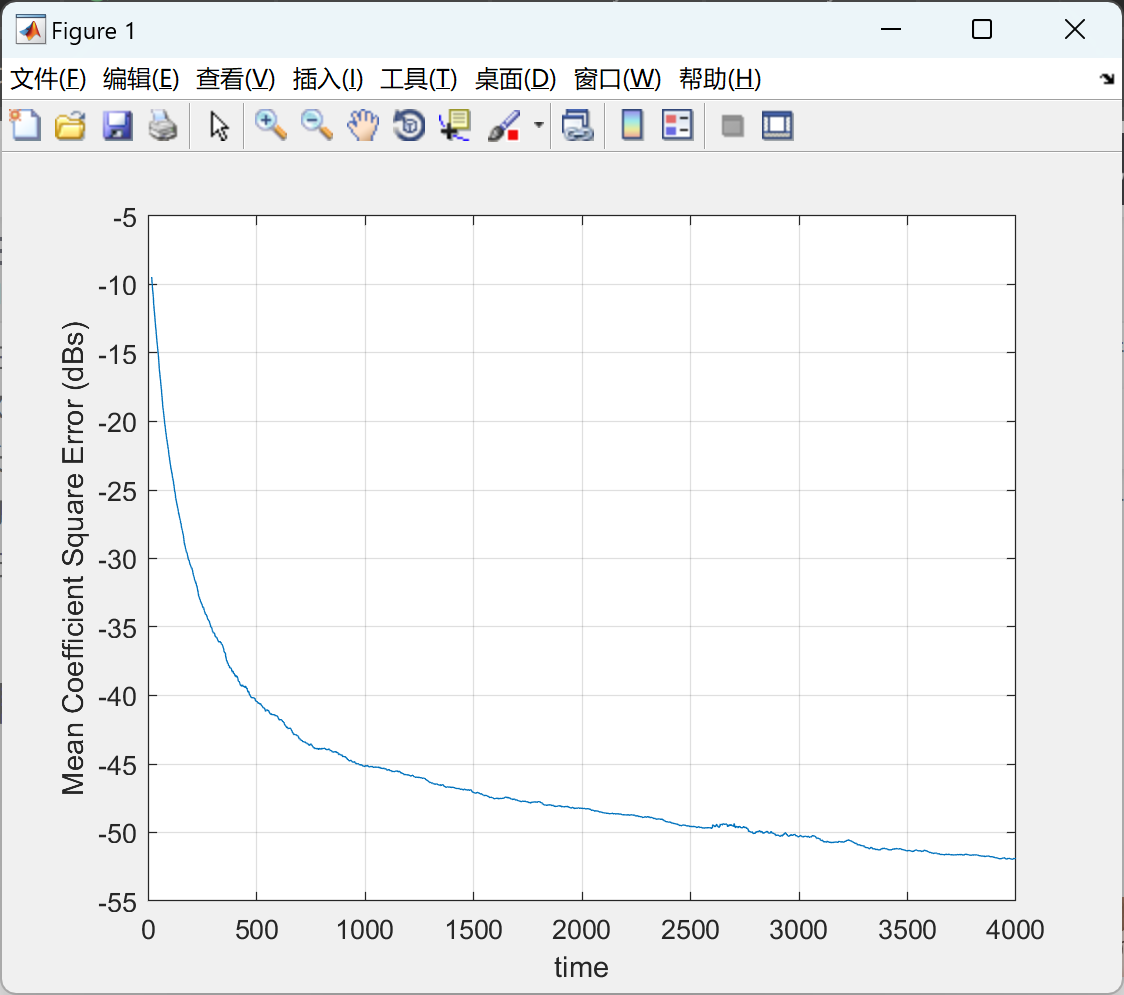
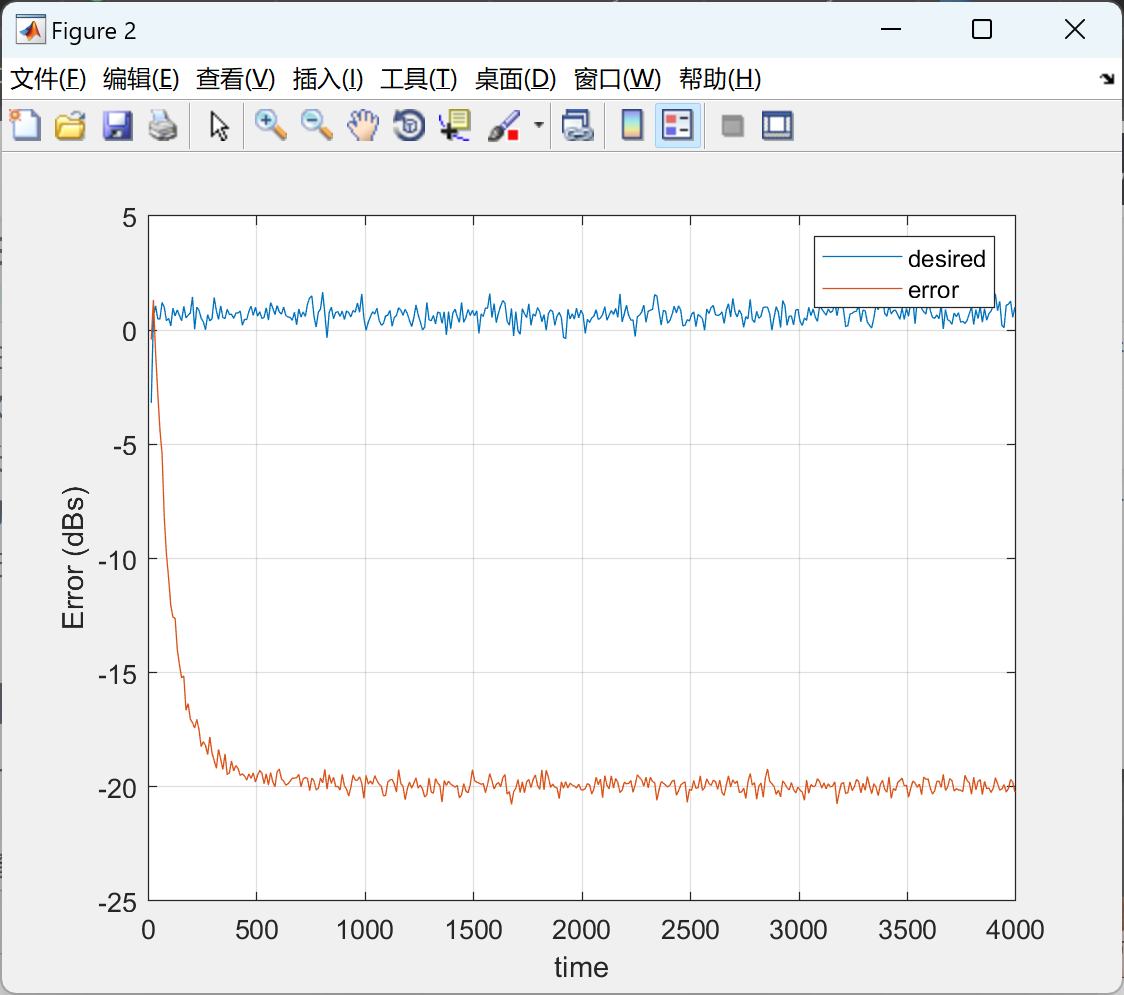
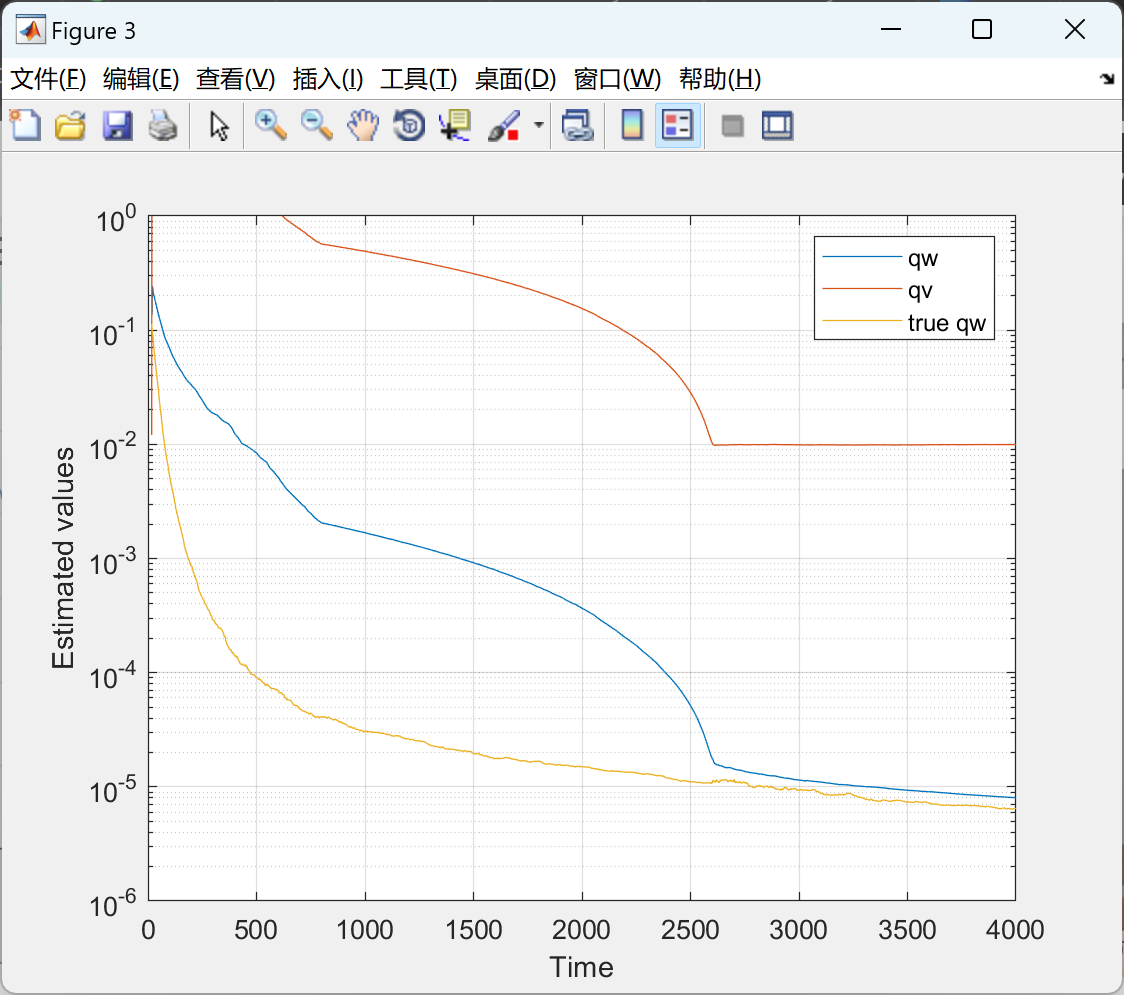
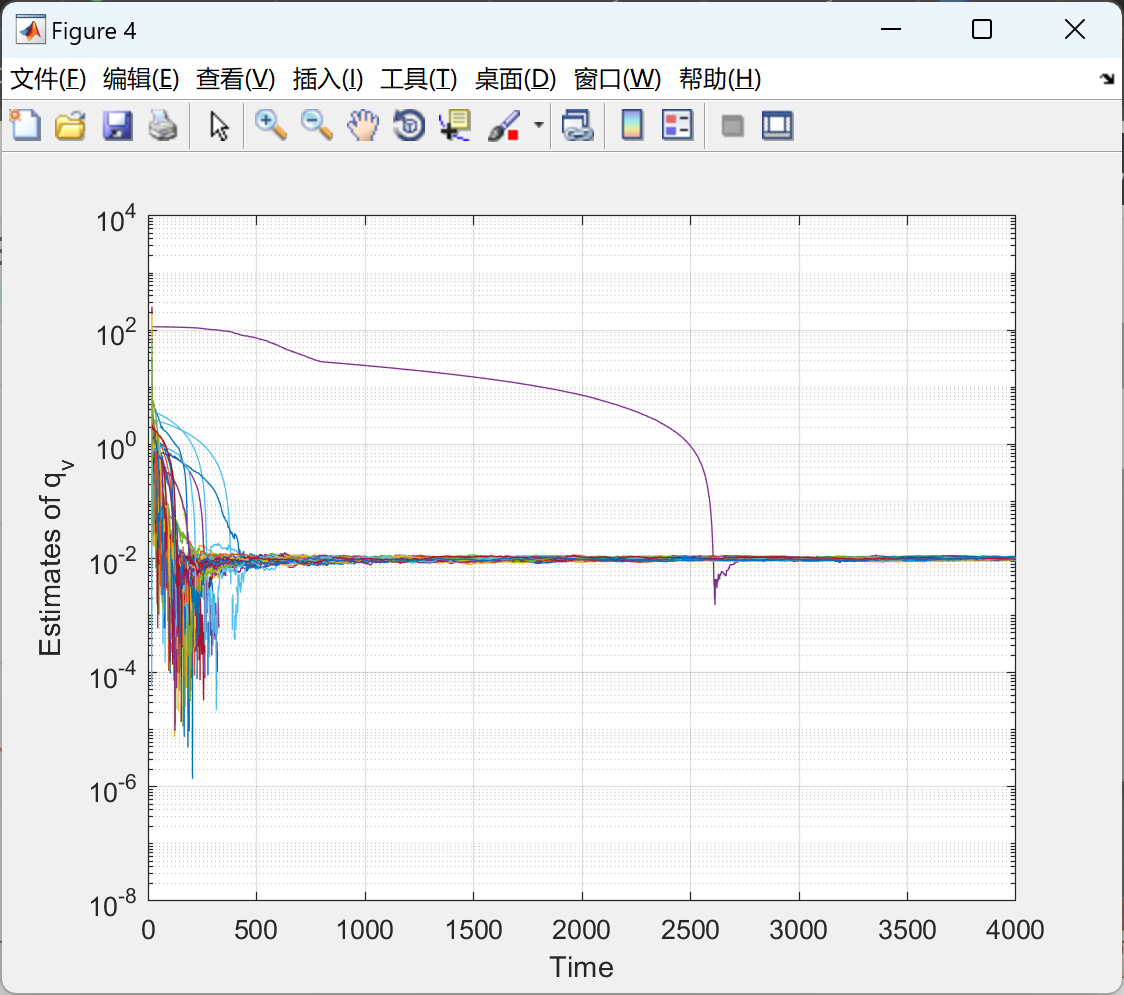
🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]F. Huang, Z. Xie and S. Zhang, "Sparse Bayesian Least-Mean-Squares Algorithm," in IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 70, no. 7, pp. 2710-2714, July 2023, doi: 10.1109/TCSII.2023.3244829.

[2]P. A. C. Lopes; A Bayesian Step Least Mean Squares Algorithm for Gaussian Signals," IEEE Signal Processing Letters, 2019