存在不稳定性的预测：我们如何知道模型是否预测良好以及如何改进它们（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

文献来源：

摘要：

本文就如何在存在不稳定性的情况下评估和提高模型的预测能力提供了指导，这些不稳定性在经济时间序列中很普遍。与经验相关的例子包括预测2007-08年的金融危机，以及更广泛地说，资产价格、汇率、产出增长和通货膨胀的波动。在不稳定环境的背景下，我讨论了如何评估模型的预测能力;如何使模型的估计更加稳健;以及如何正确报告预测不确定性的衡量标准。重要的是，也许令人惊讶的是，模型参数的中断既不必要，也不足以在模型的预测性能中产生时间变化：因此，不应测试模型参数的中断，而应以稳健的方式评估其预测能力。此外，对模型预测性能的局部测量比传统的平均测量更合适。

关键词：

模型构建与估计 预测模型 模拟方法 价格水平 通货膨胀 通货紧缩 业务波动 周期 价格 和周期：预测和模拟：模型和应用 国际金融预测与模拟：模型与应用

📚2 运行结果

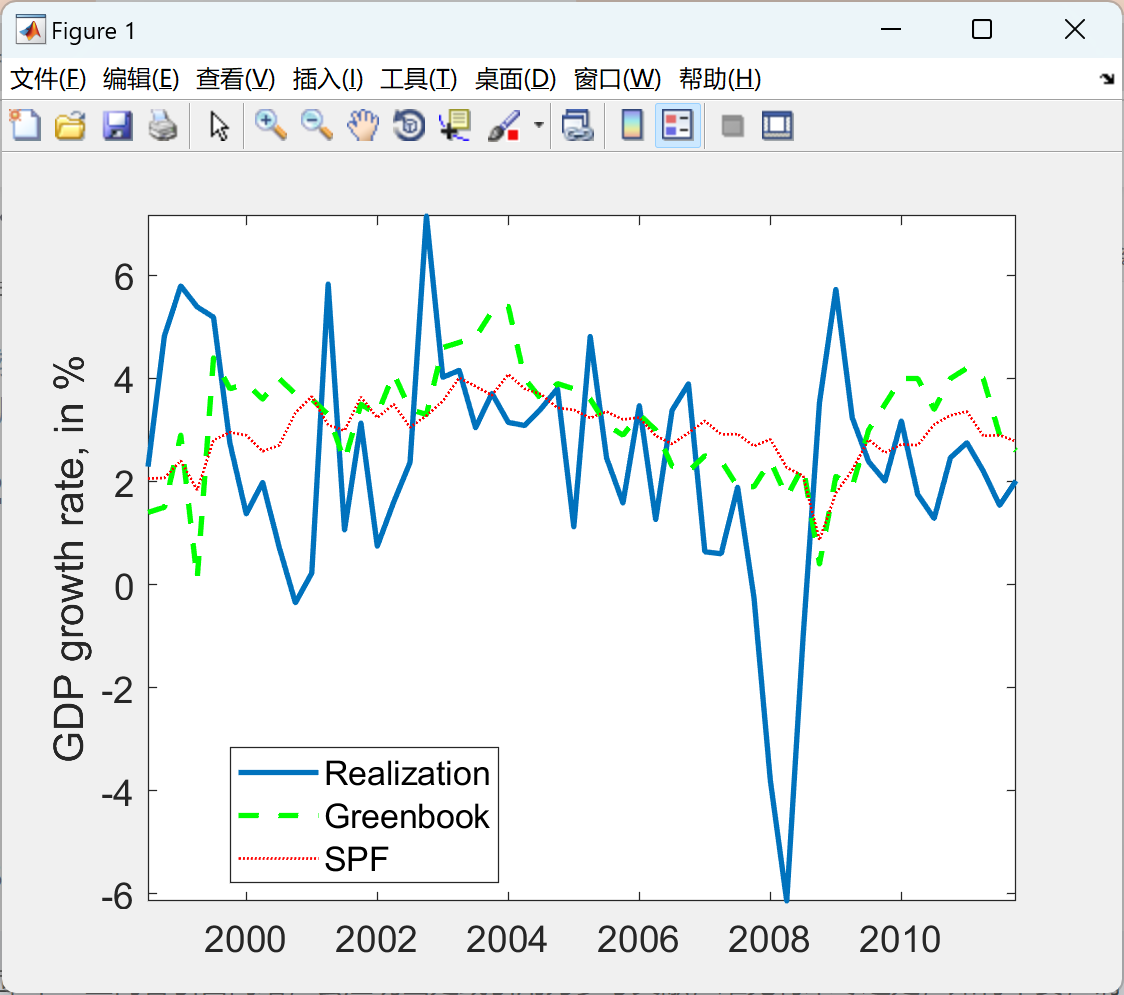
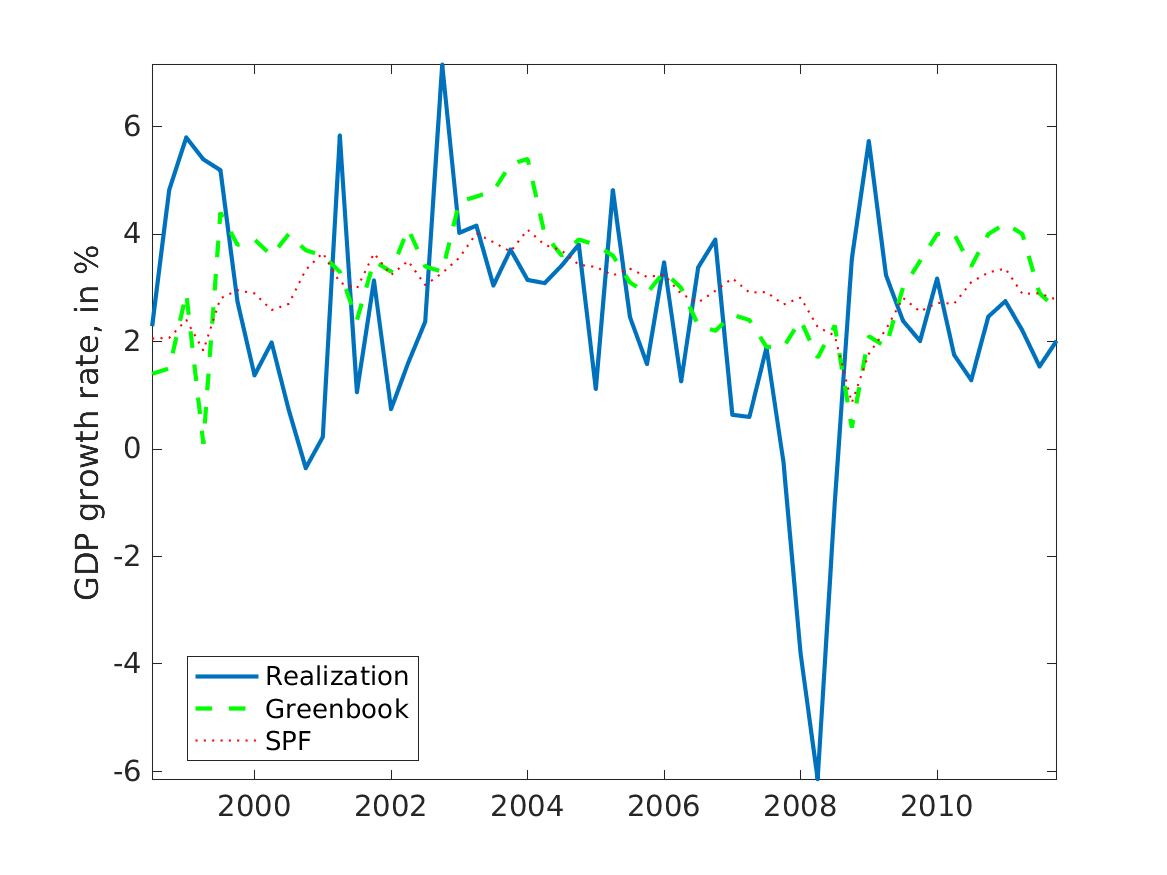
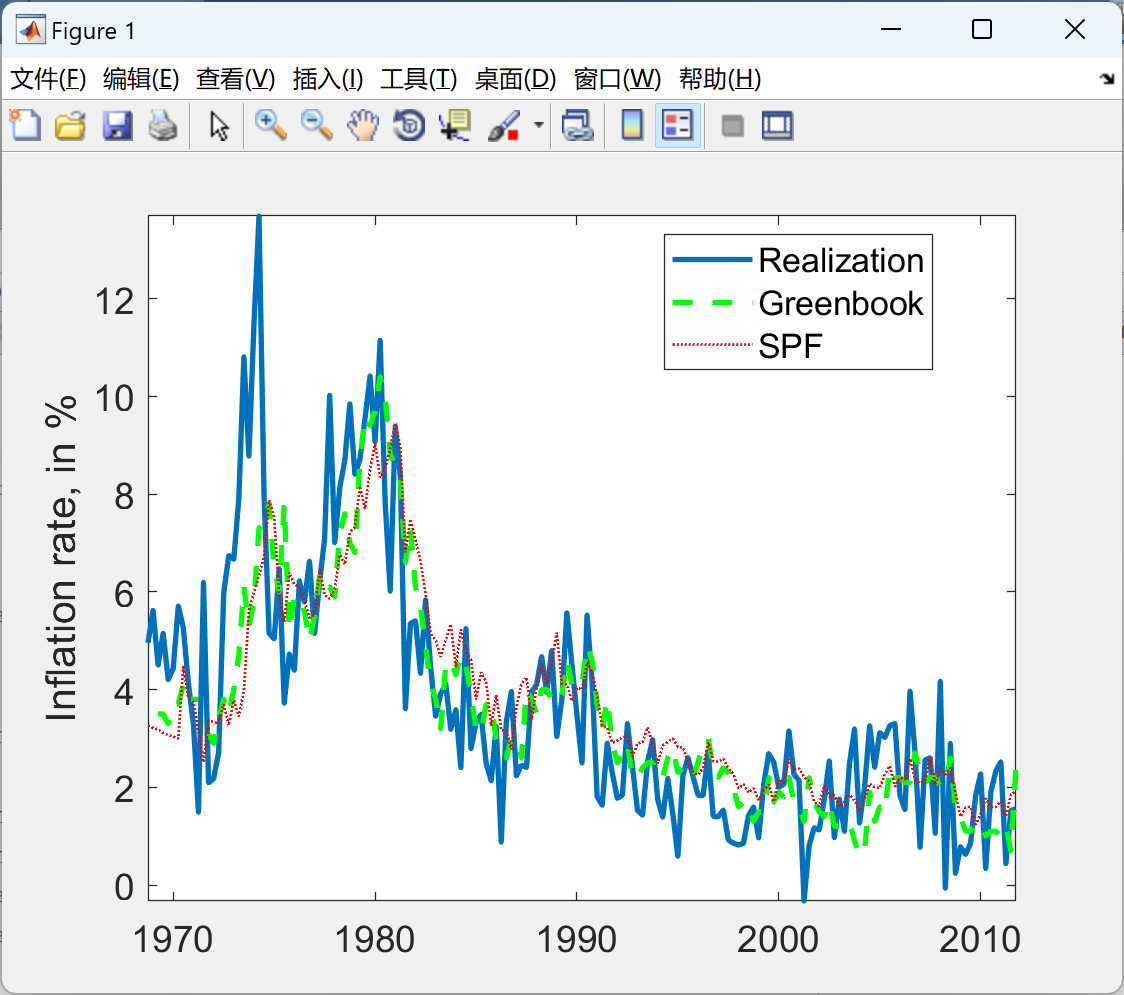
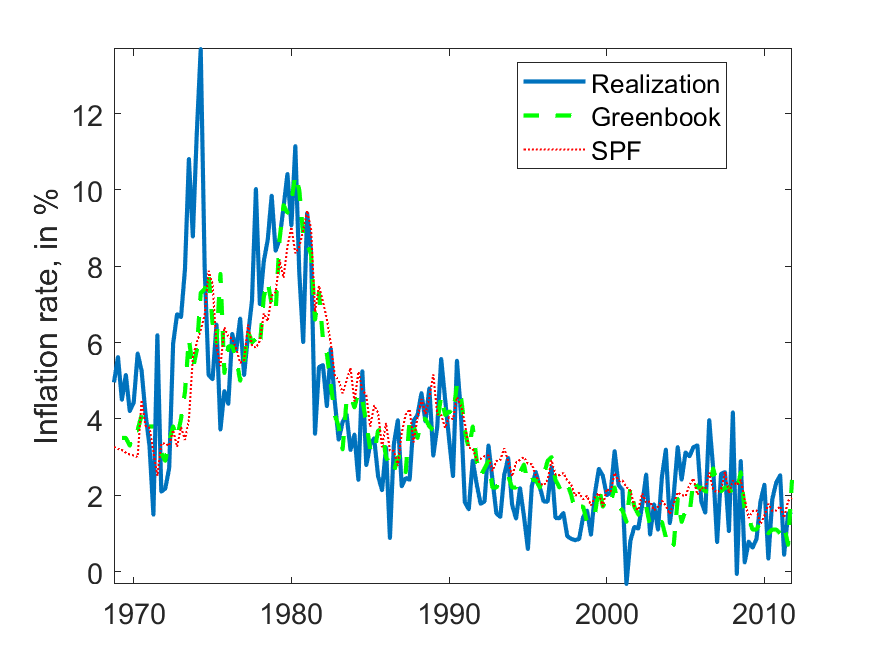
后面其他运行结果图全部去掉Matlab图框。

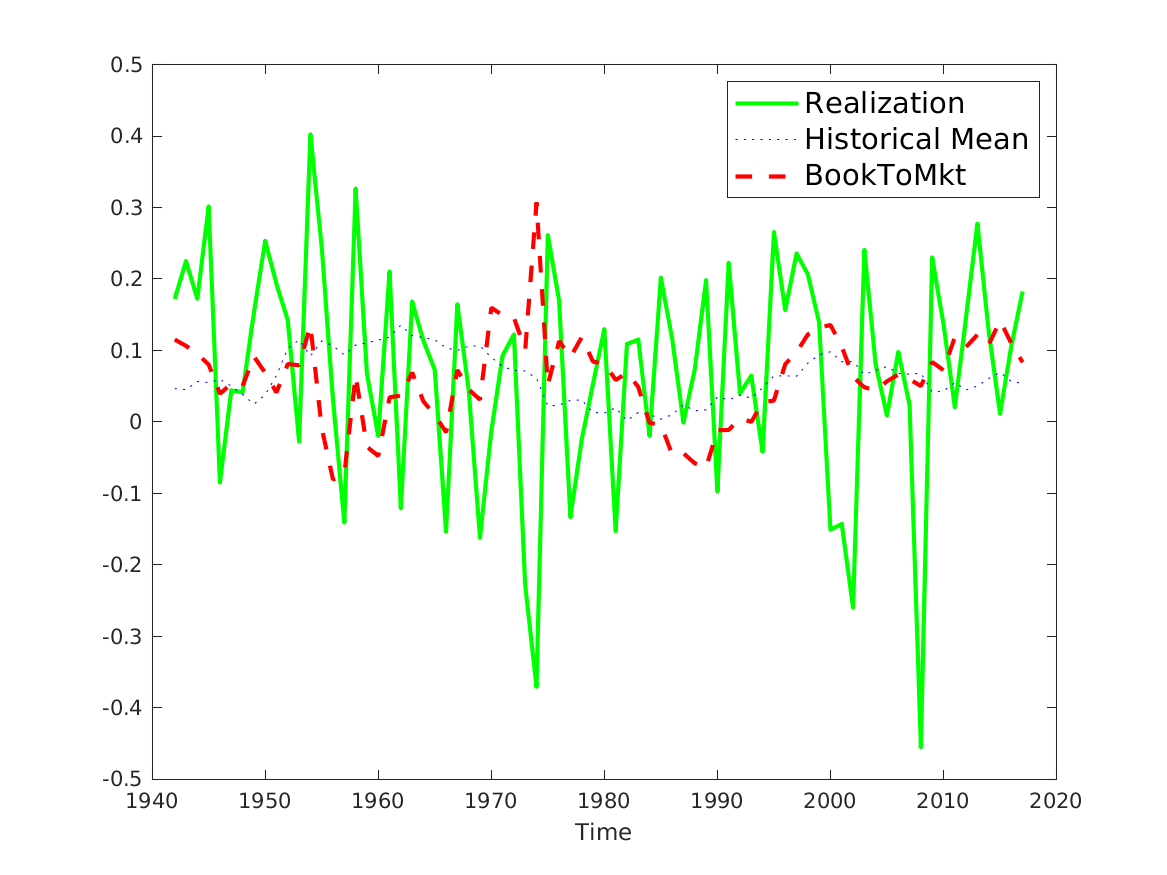
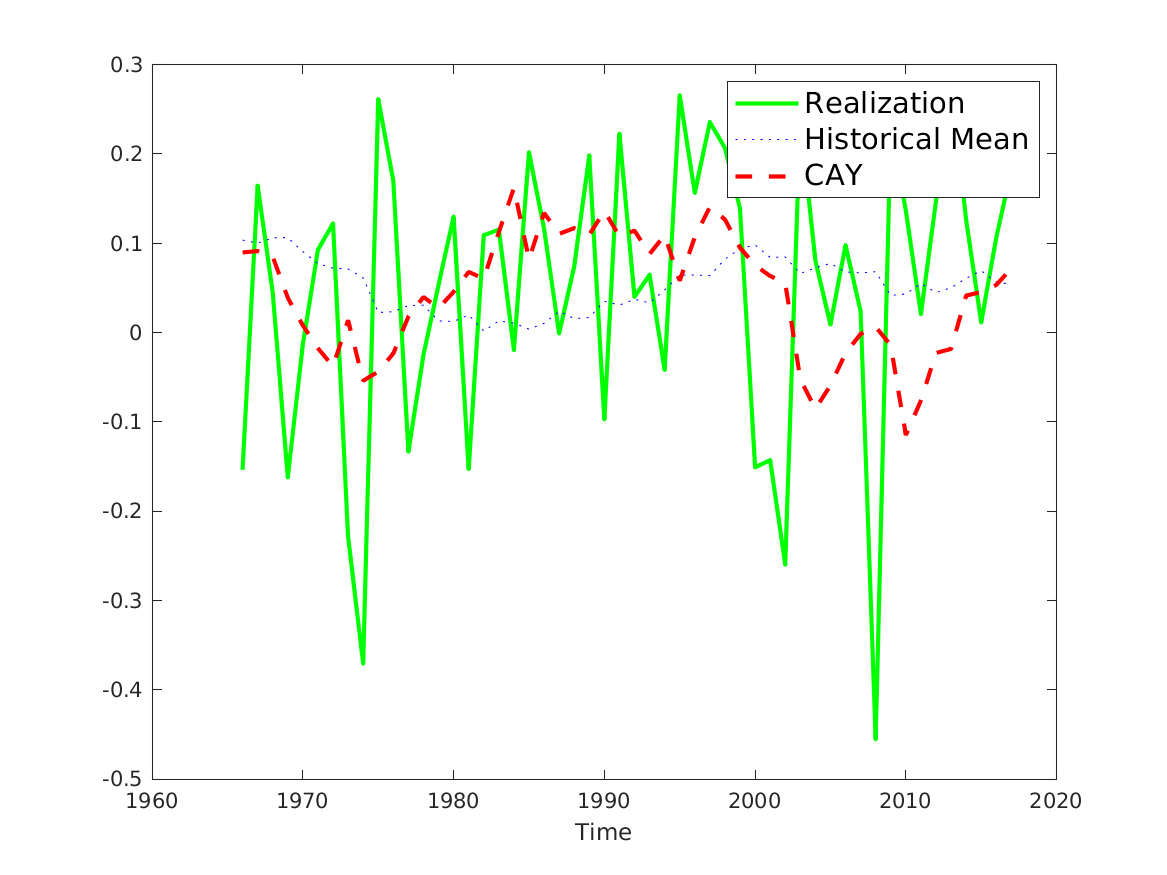
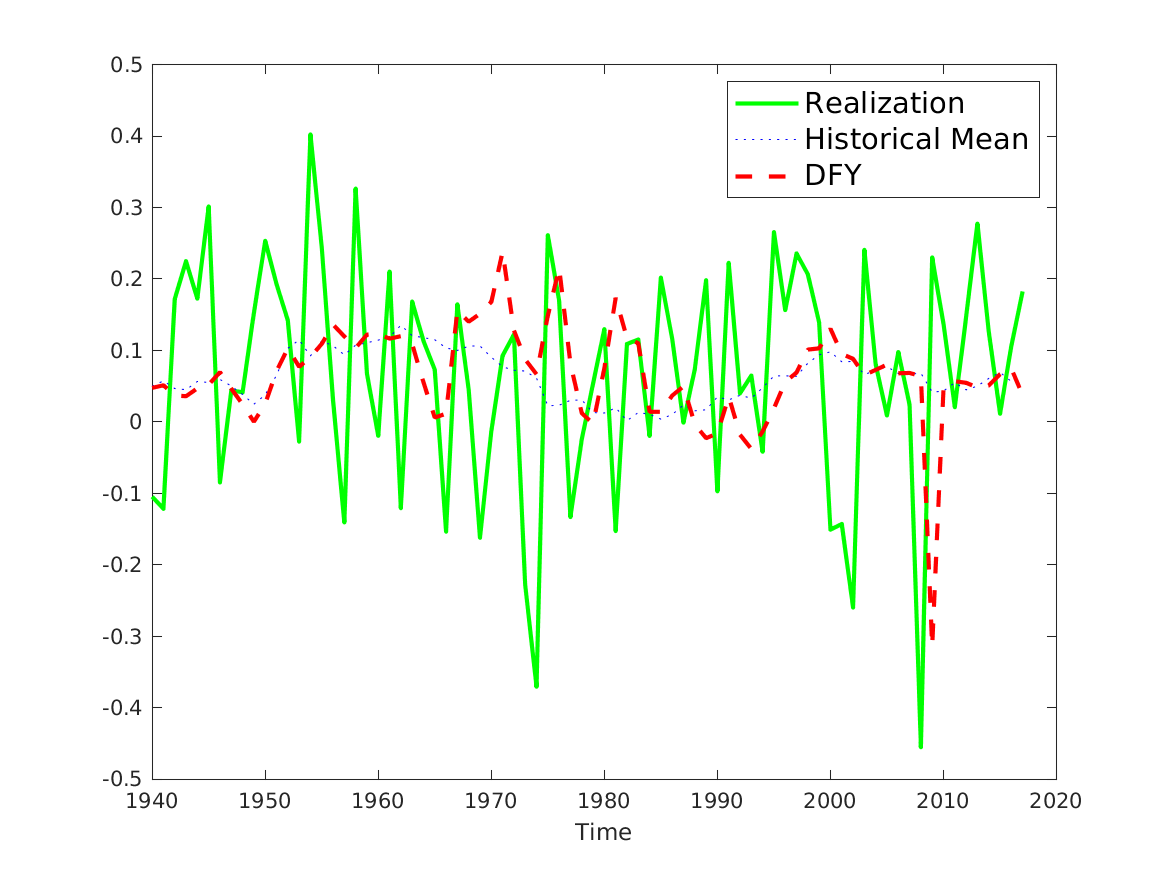
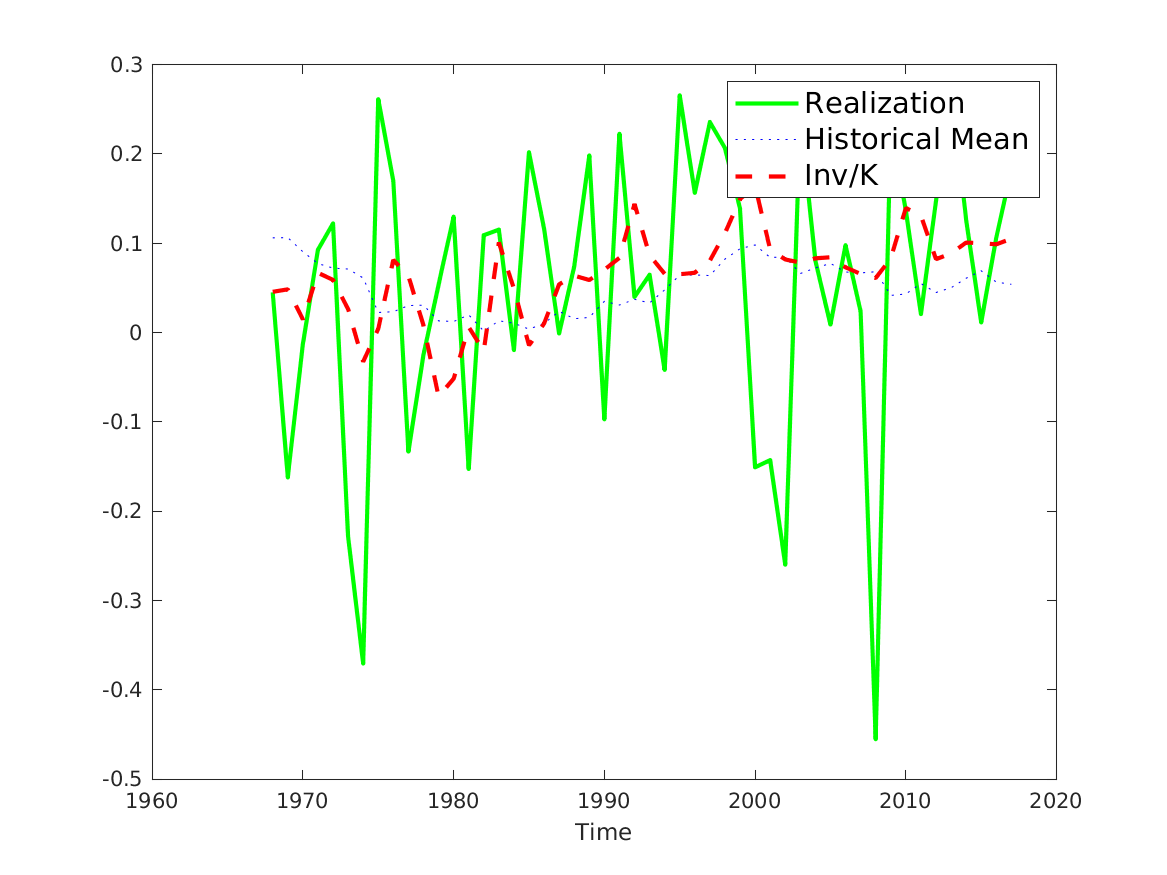
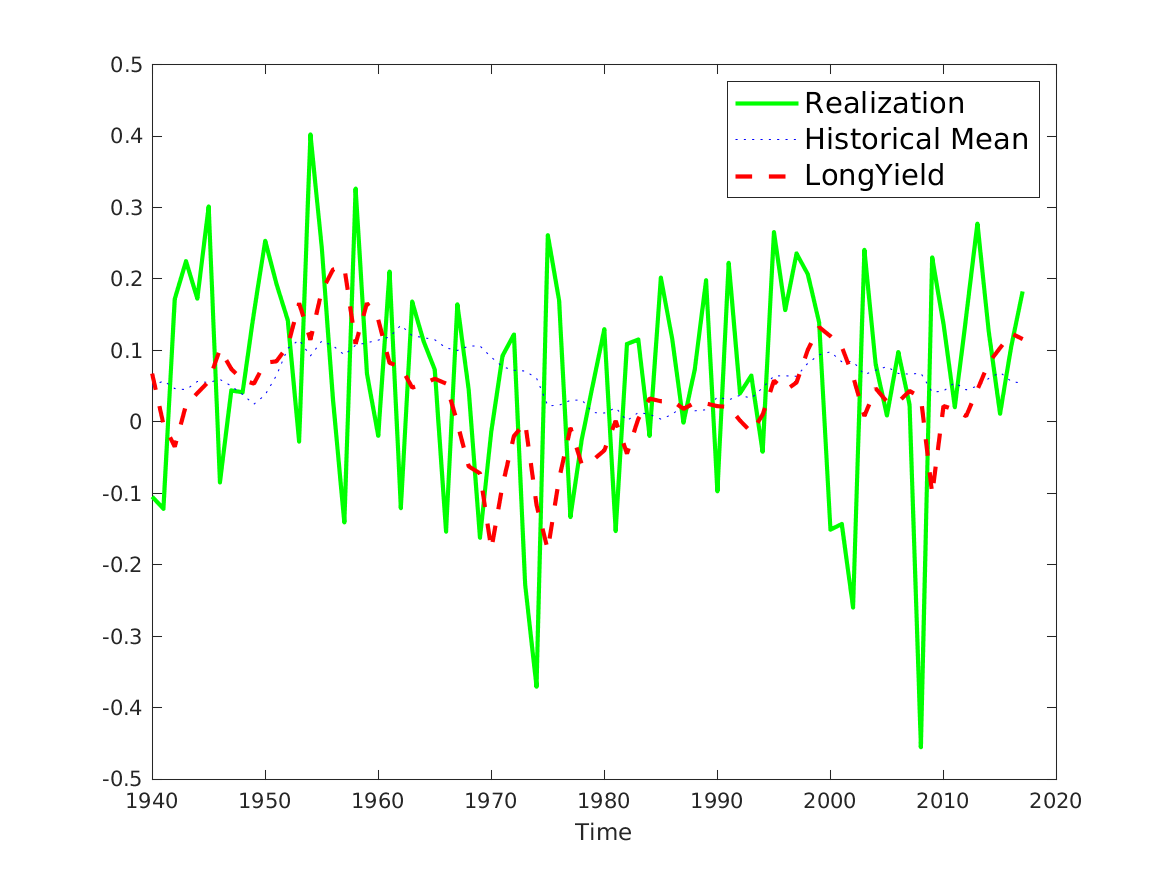
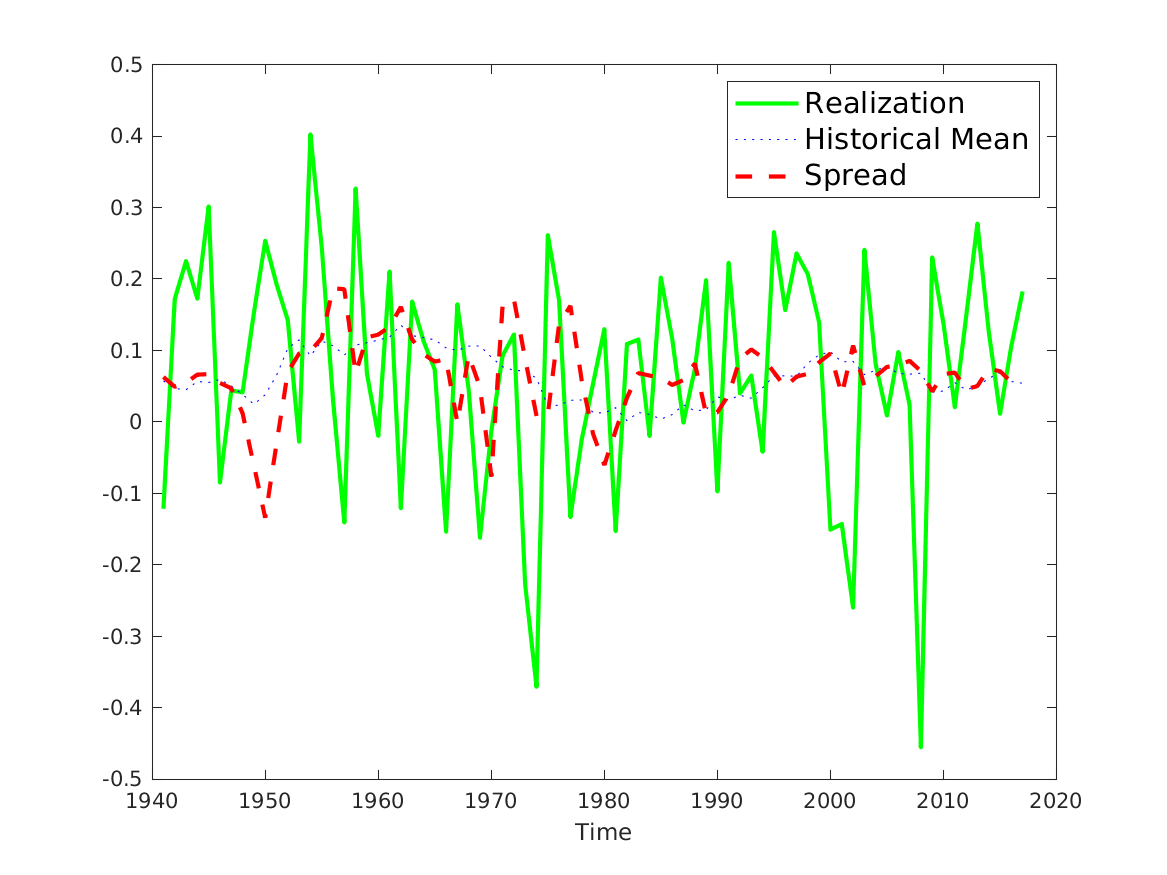
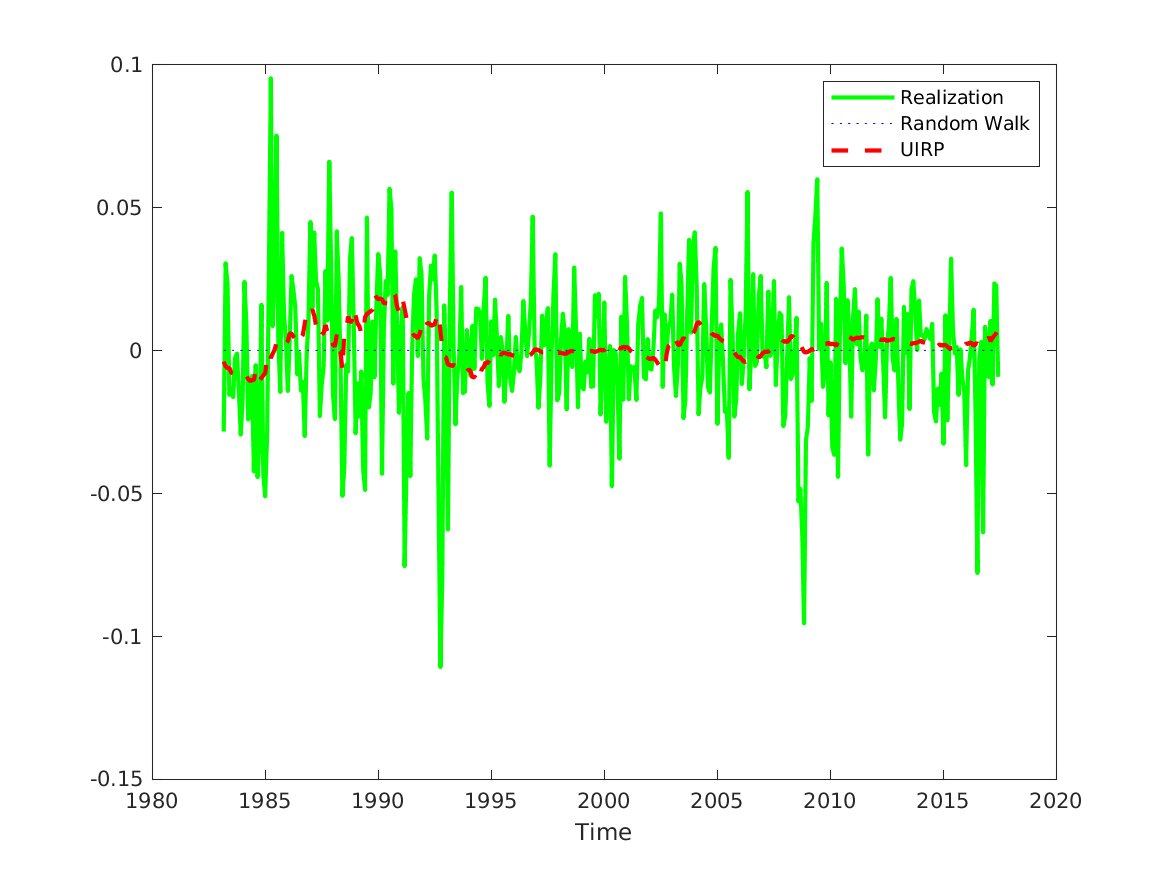
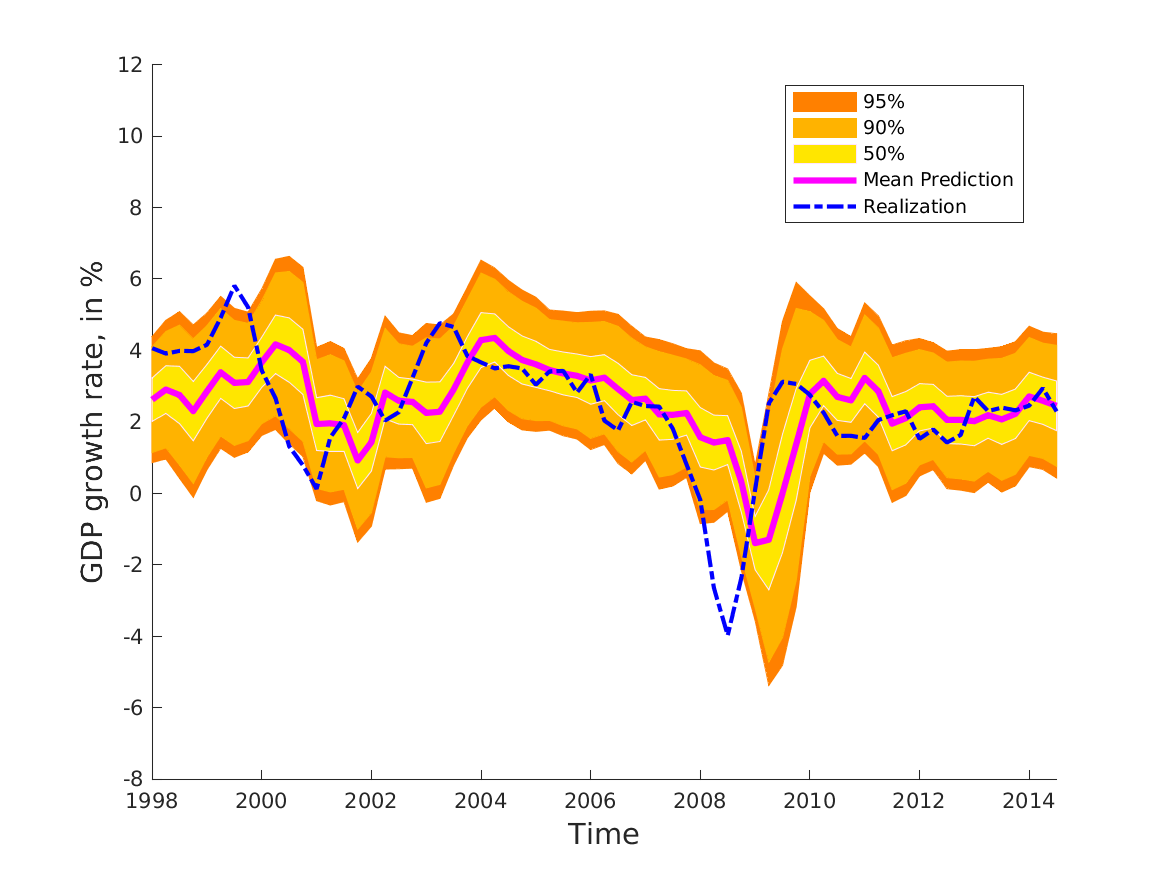
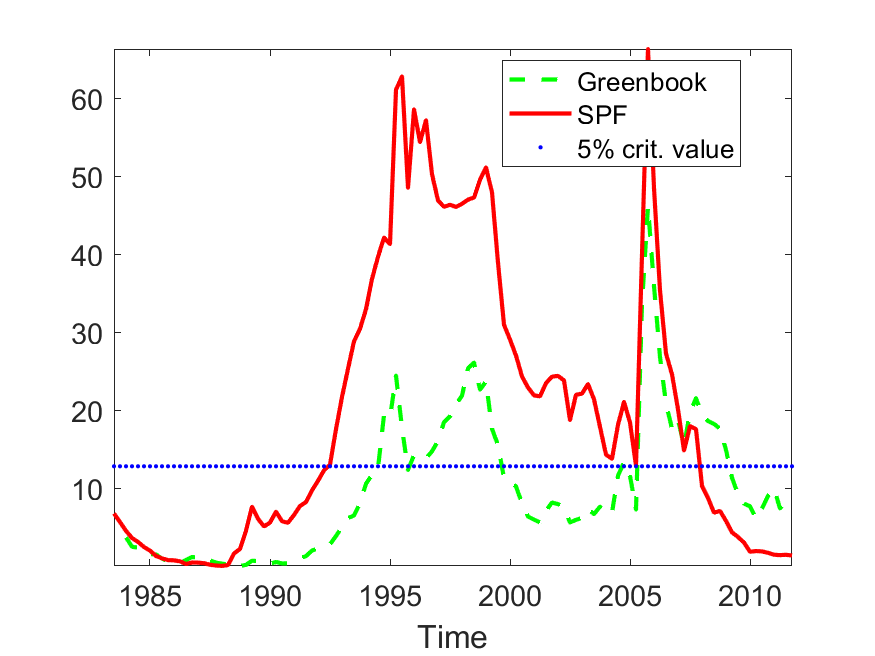
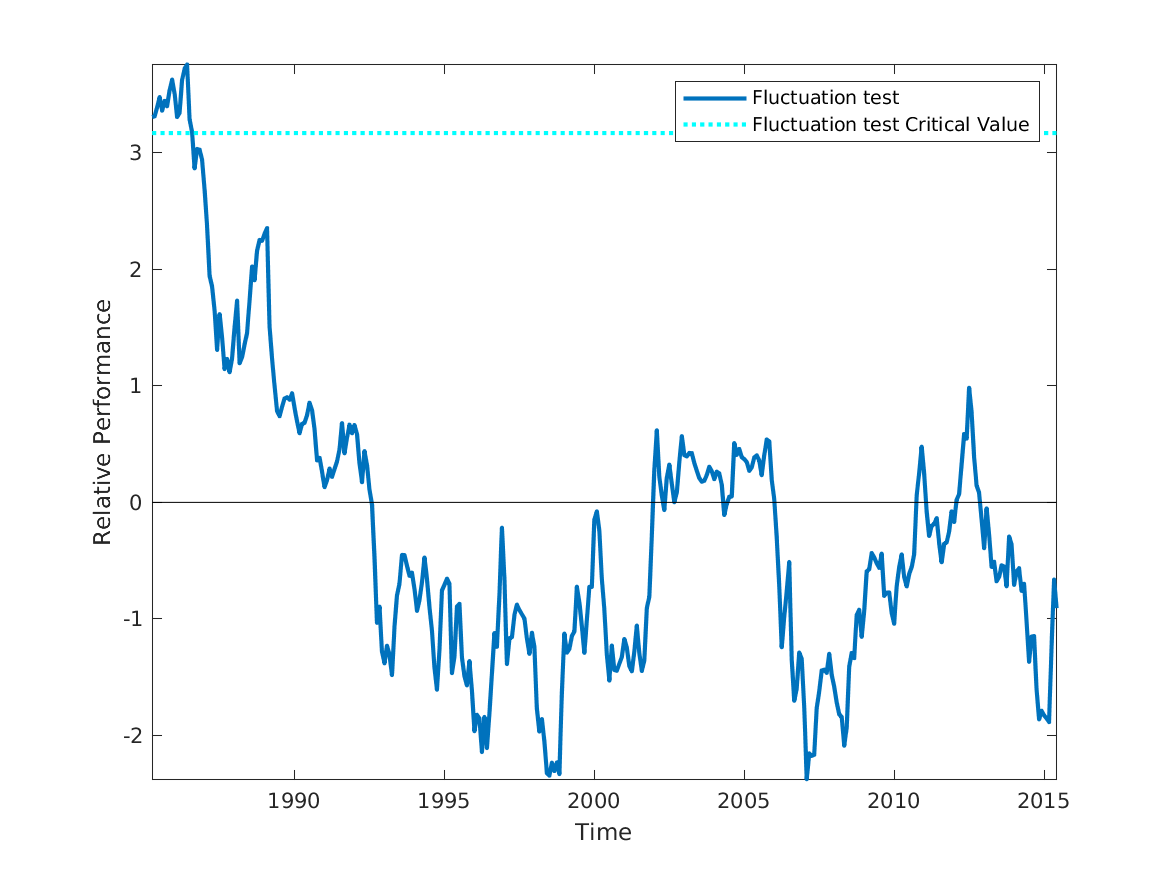
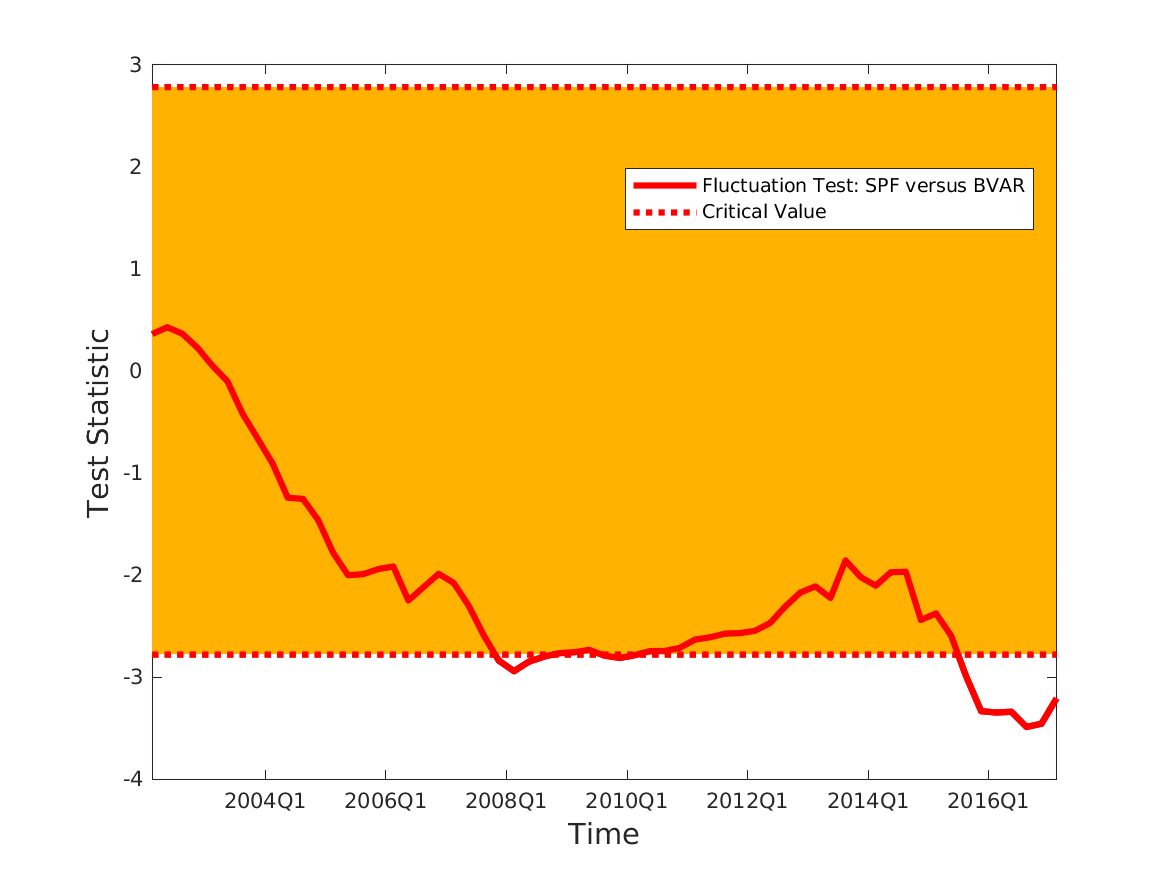
 部分代码：

fn=figure
    timehere=[t0:0.25:T]; 
    initial=67; avg=average.mu; avs=average.sigma;
    h1 = patch([(timehere(:,initial:end)) flip(timehere(:,initial:end))],[(avg(initial:end,:) + 1.96*avs(initial:end,:))' flip((avg(initial:end,:) - 1.96*avs(initial:end,:)))'],[1 0.5 0],'Edgecolor',[1 0.5 0]);
    hold on
    h2 = patch([(timehere(:,initial:end)) flip(timehere(:,initial:end))],[(avg(initial:end,:)+1.645*avs(initial:end,:))' flip((avg(initial:end,:)-1.645*avs(initial:end,:))')],[1 0.7 0],'Edgecolor',[1 0.7 0]);
    hold on
    h3 = patch([(timehere(:,initial:end)) flip(timehere(:,initial:end))],[(avg(initial:end,:)+0.6745*avs(initial:end,:))' flip((avg(initial:end,:)-0.6745*avs(initial:end,:))')],[1 0.9 0],'Edgecolor',[1 0.9 1]);
    hold on
    h4 = plot(timehere(:,initial:end),avg(initial:end,:)','-m','Linewidth',3);
    hold on
    h5 = plot(timehere(:,initial:end),realizeddata(initial:end-3,4)','-.b','Linewidth',2);
    legend([h1 h2 h3 h4 h5], {'95%','90%','50%','Mean Prediction','Realization'},'Location','Best')
    xlim([min(timehere(:,initial:end)) max(timehere(:,initial:end))])
    ylim([-8 12])
    ylabel('GDP growth rate, in %'); xlabel('Time');
    set(findall(gcf,'Type','text'),'FontSize',14)
    saveas(fn,'../results/Figure5.png')

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

🌈4 Matlab代码实现