机会约束规划技术研究（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

机会约束规划（Chance Constrained Programming）是指约束条件中含有随机变量，且必须在预测到随机变量的实现之前作出决策的情况下；而且还要考 虑到所作决策在不利情况发生时可能不满足约束条件，这时要采用

一种原则，即允许所作决策在一定程度上不满足约束条件，但该决策应使约束条件成立的概率不小于某一置信水平。

随机规划的三个分支是期望值模型、机会约束规划和相关机会规划。其中机会约束规划是由查纳斯（A.Charnes）和库伯（W.W.Cooper）于1959年提出的，是在一定的概率意义下达到最优的理论。它是一种随机规划方法，针对约束条件中含有随机变量，并且必须在观测到随机变量的实现之前做出决策的问题。

机会约束规划考虑到所做决策在不利的情况发生时可能不满足约束条件，而采用一种原则：即允许所做决策在一定程度上不满足约束条件，但该决策使约束条件成立的概率不小于某一个足够小的置信水平。对一些特殊情况，机会约束规划问题可以转化为等价的确定性数学规划问题，但对于较复杂的机会约束规划问题，则要利用基于随机模拟的遗传算法来求解一般机会约束规划问题以及机会约束多目标规划和机会约束目标规划问题。

机会约束规划的解法大致有两种。其一，将机会约束规划转化为确定性规划，然后用确定性规划的理论去解决；其二，通过随机模拟技术处理机会约束条件，并利用遗传算法的优胜劣汰，得到机会约束规划的目标函数最优值和决策变量最优解集。

机会约束规划的目标函数最优值及决策变量的最优解集与模型中的随机系数有关，因而具有随机性。从数理统计的角度看，对这种随机的目标函数最优值以及决策变量的最优解集可以作出某种置信水平的区间估计。衡量区间估计的精度的一个重要指标是估计区间的长度，估计区间长度越小，估计精度就越大；反之，估计区间长度越大，估计精度就越小。​

📚2 运行结果

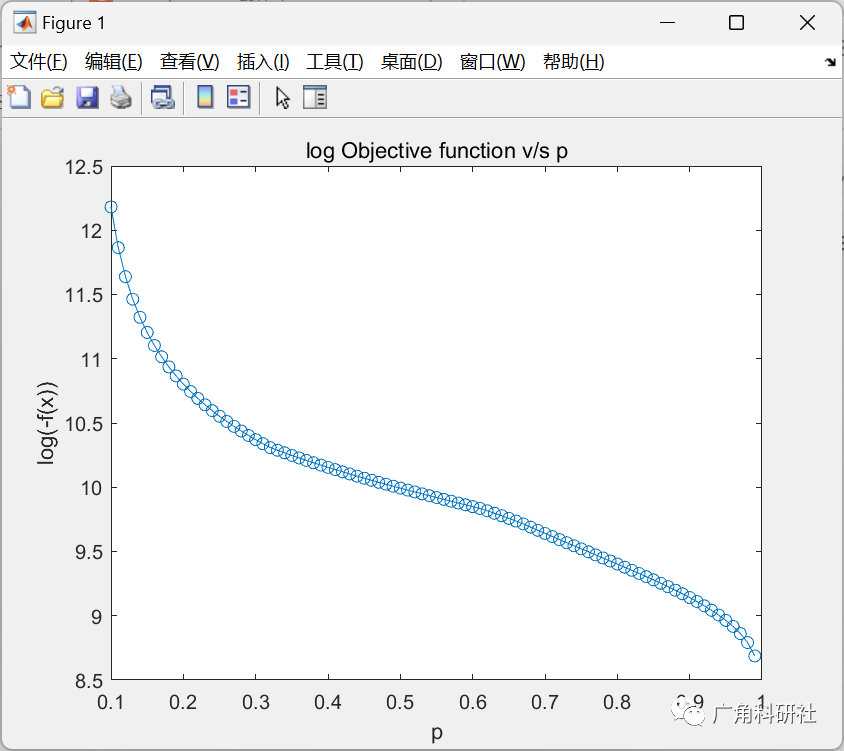
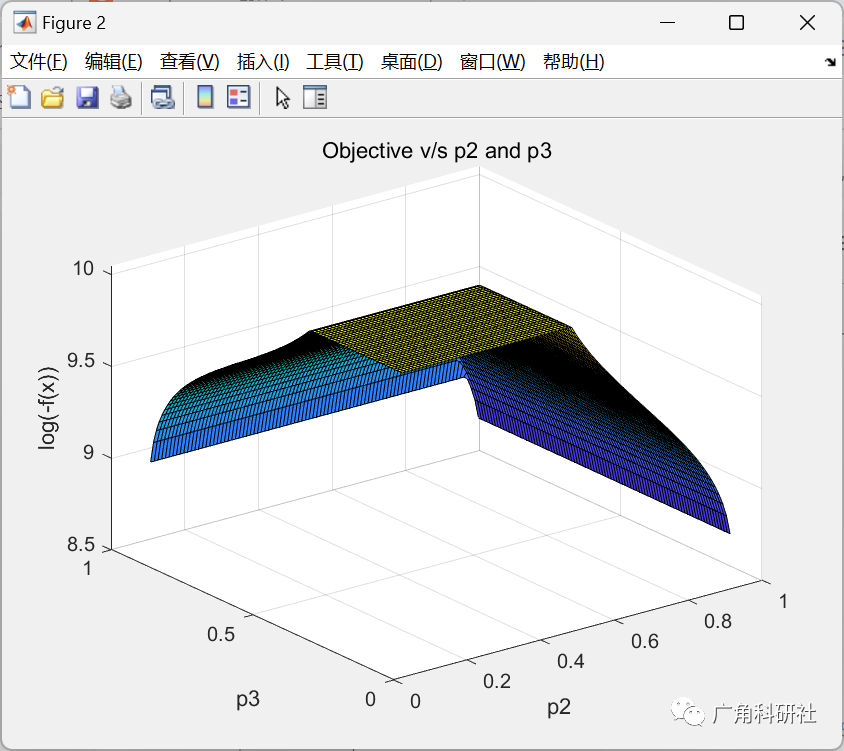
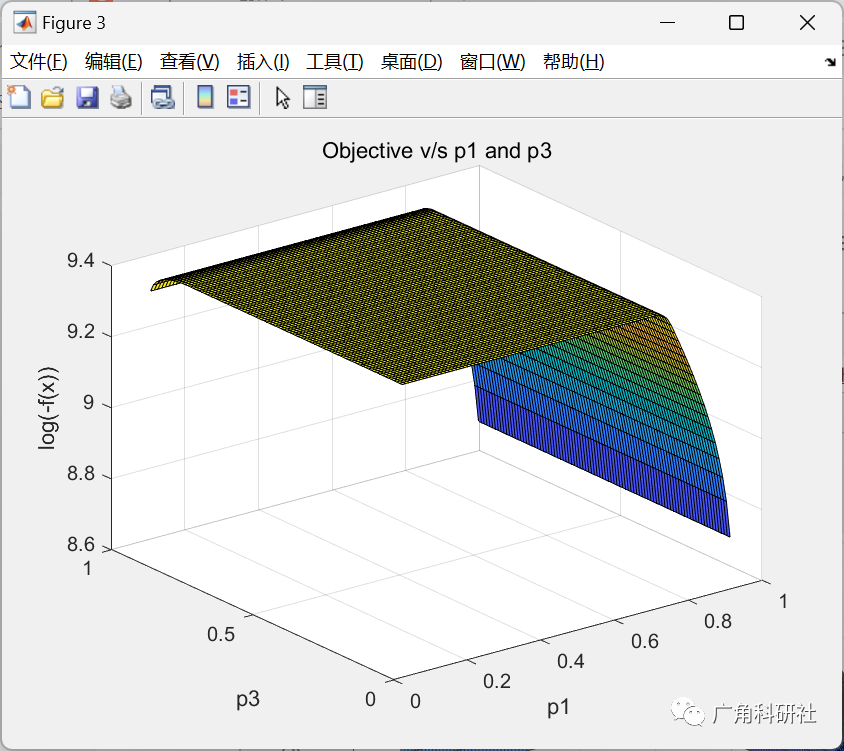
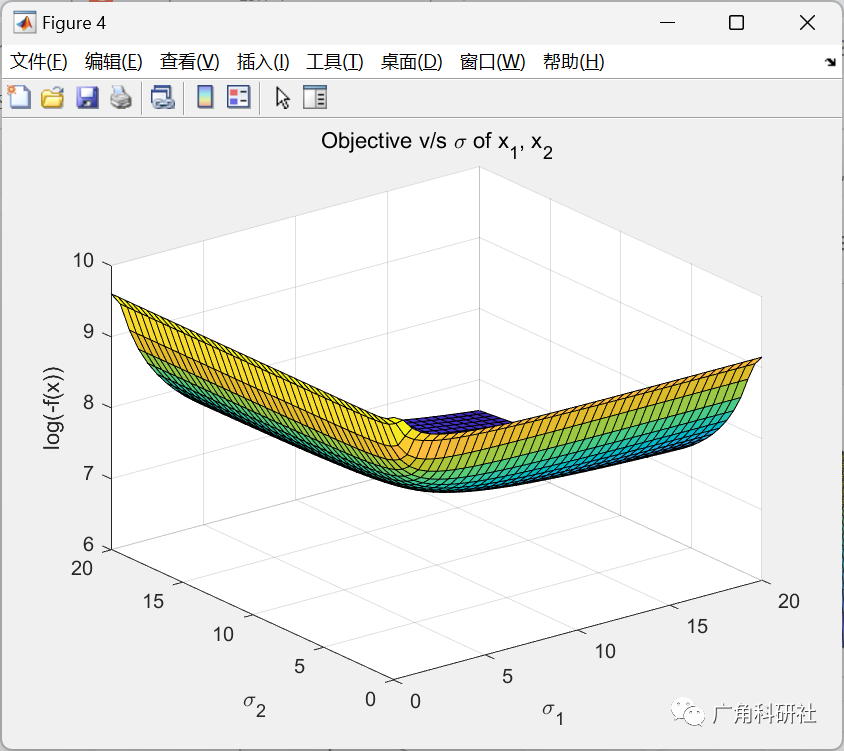
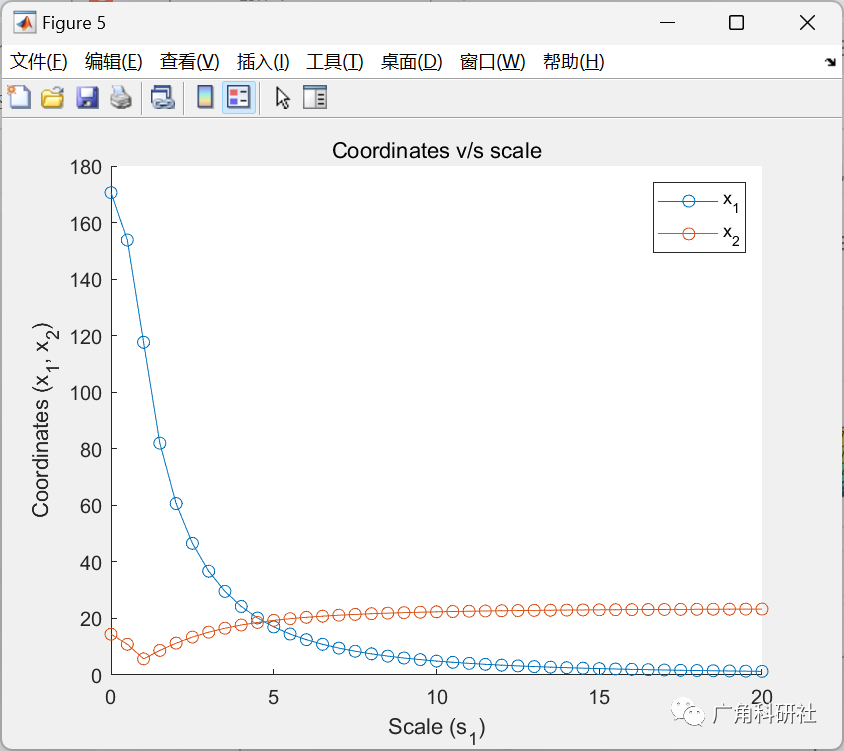
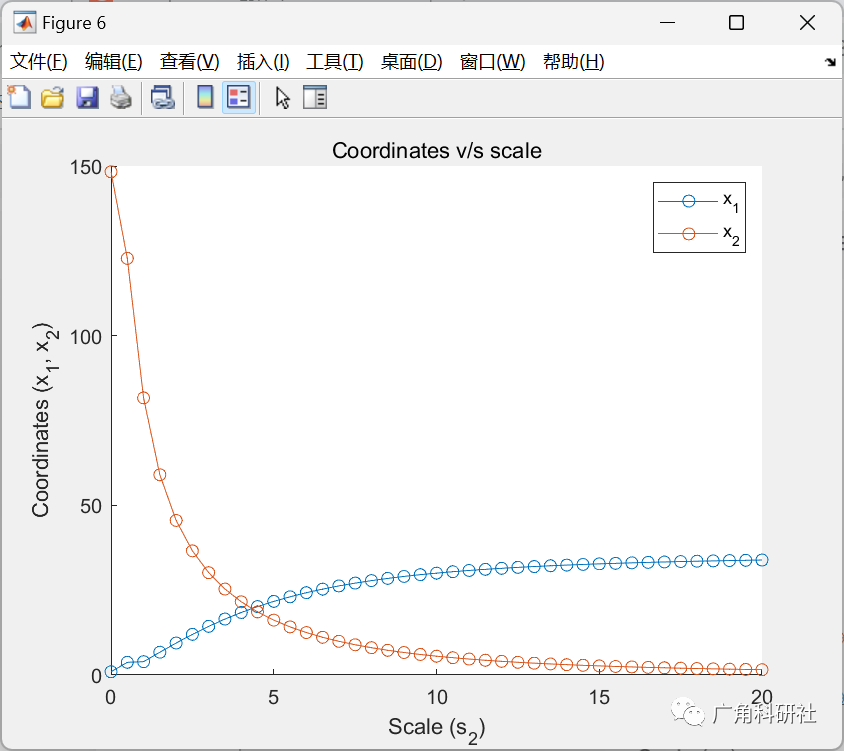
主函数部分代码：

close all;
clear;
clc;
​
% Read from file
filename = 'problems/problem1.txt';
[n, m, k, cm, cs, Am, bm, As, bs, p] = read_from_file(filename);
% n = number of x_i
% m = number of constraints
lb = zeros(n, 1);
x0 = zeros(n, 1);
​
% Do analysis
prange = 0.1:0.01:0.99;
PR = length(prange);
% Check sensitivity to all P
xv = zeros(length(prange), n);
obj = zeros(length(prange), 1);
options = optimoptions('fmincon', 'Display', 'off');
for i = 1:length(prange),
    p(1) = prange(i);
    p(2) = prange(i);    
    p(3) = prange(i);
    fprintf('Solving for p3 = %f\n', prange(i));
    [x, fval] = fmincon(@(x)get_objective(x, cm, cs, k), x0, [], [], [], [], lb, [], @(x)get_constraints(x, m, Am, As, bm, bs, p), options);
    xv(i, :) = x + 0;
    obj(i, :) = fval;
end
​
% Check sensitivity to P2 and P3
prange = 0.1:0.01:0.99;
[ppx, ppy] = meshgrid(prange, prange);
PR = length(prange);
%
p(1) = 0.9;
objP2P3 = zeros(PR, PR);
for i = 1:PR,
    for j = 1:PR,
        p(2) = prange(i);
        p(3) = prange(j);
        fprintf('Solving for p1 = %f, p2 = %f\n', prange(i), prange(j));    
        [x, fval] = fmincon(@(x)get_objective(x, cm, cs, k), x0, [], [], [], [], lb, [], @(x)get_constraints(x, m, Am, As, bm, bs, p), options);
        objP2P3(i, j) = fval;
    end
end
​
% Check sensitivity to P1 and P3
prange = 0.1:0.01:0.99;
[ppx, ppy] = meshgrid(prange, prange);
PR = length(prange);
%
p(2) = 0.9;
objP1P3 = zeros(PR, PR);
for i = 1:PR,
    for j = 1:PR,
        p(1) = prange(i);
        p(3) = prange(j);
        fprintf('Solving for p1 = %f, p2 = %f\n', prange(i), prange(j));    
        [x, fval] = fmincon(@(x)get_objective(x, cm, cs, k), x0, [], [], [], [], lb, [], @(x)get_constraints(x, m, Am, As, bm, bs, p), options);
        objP1P3(i, j) = fval;
    end
end
​
​
%% Check sensitivity to variances of x1
p = p*0 + 0.9;
scales = 0:0.5:20;
S = length(scales);
objscale = zeros(S, S);
% x1, x2 stores
x_var = zeros(S, S, 2);
% Run for some scales
for i = 1:length(scales),
    for j = 1:length(scales),
        As_tmp = As;
        As_tmp(:, 1) = As(:, 1)*scales(i);
        As_tmp(:, 2) = As(:, 2)*scales(j);
        [x, fval] = fmincon(@(x)get_objective(x, cm, cs, k), x0, [], [], [], [], lb, [], @(x)get_constraints(x, m, Am, As_tmp, bm, bs, p), options);
        objscale(i, j) = fval;
        x_var(i, j, :) = x;
    end
end

🎉3 参考文献

[1]麻倩倩. 一类随机机会约束规划的算法及应用研究[D].华北电力大学（河北）,2007.

部分理论引用网络文献，若有侵权联系博主删除。

🌈4 Matlab代码实现