本文详细解析了如何使用动态规划方法解决寻找字符串中最长回文子串的问题，通过状态定义、状态转移方程及初始化的深入探讨，提供了一种高效求解策略。
题目描述
给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。题目难度中等
示例1：
输入: “babad”
输出: “bab”
注意: “aba” 也是一个有效答案。
实例2
输入: “cbbd”
输出: “bb”
动态规划基础（啰里吧嗦的一些说明）
- 思考状态（重点）
- 状态的定义，先尝试「题目问什么，就把什么设置为状态」；
- 然后思考「状态如何转移」，如果「状态转移方程」不容易得到，尝试修改定义，目的依然是为了方便得到「状态转移方程」。
「状态转移方程」是原始问题的不同规模的子问题的联系。即大问题的最优解如何由小问题的最优解得到。
- 思考状态转移方程（核心、难点）
-
状态转移方程是非常重要的，是动态规划的核心，也是难点；
-
常见的推导技巧是：分类讨论。即：对状态空间进行分类；
-
归纳「状态转移方程」是一个很灵活的事情，通常是具体问题具体分析；
-
除了掌握经典的动态规划问题以外，还需要多做题；
-
如果是针对面试，请自行把握难度。掌握常见问题的动态规划解法，理解动态规划解决问题，是从一个小规模问题出发，逐步得到大问题的解，并记录中间过程；
-
「动态规划」方法依然是「空间换时间」思想的体现，常见的解决问题的过程很像在「填表」。
- 思考初始化
初始化是非常重要的，一步错，步步错。初始化状态一定要设置对，才可能得到正确的结果。
-
角度 1：直接从状态的语义出发；
-
角度 2：如果状态的语义不好思考，就考虑「状态转移方程」的边界需要什么样初始化的条件；
-
角度 3：从「状态转移方程」方程的下标看是否需要多设置一行、一列表示「哨兵」（sentinel），这样可以避免一些特殊情况的讨论。
- 思考输出
有些时候是最后一个状态，有些时候可能会综合之前所有计算过的状态。
-
思考优化空间（也可以叫做表格复用）
-
「优化空间」会使得代码难于理解，且是的「状态」丢失原来的语义，初学的时候可以不一步到位。先把代码写正确是更重要；
-
「优化空间」在有一种情况下是很有必要的，那就是状态空间非常庞大的时候（处理海量数据），此时空间不够用，就必须「优化空间」；
非常经典的「优化空间」的典型问题是「0-1 背包」问题和「完全背包」问题。
原文出处
本题使用动态规划
1.定义状态，在本题中的状态是什么，怎么表示？
是不是比较抽象，没关系，让我举个栗子，现在有个回文子串（不知道回文子串的童鞋可以看我的另外一篇博客），例如是aabbaa，让我们填个表先。图片有些大，我不太会调 。
纵坐标1-6代表子串的起始位置，横坐标1-6代表子串的终止位置。我令这个表为P，若是P[i，j]等于1代表从i到j是回文子串，反之不是回文子串。大家可以自己画一画。这个表就是状态表,我们只用到整个二维数组的一半，写程序的时候需要注意。从这个表可以看出第一行第六列为1，所以最长的回文字符串就是aabbaa。
2.状态转移方程，花里胡哨的名称，明明就是填表规则
若是P(i,j)为回文子串必须满足两个条件P(i+1,j−1)和Si与Sj字符相同，这个可以很容易理解，即用式子表示为如下
> P(i,j)=P(i+1,j−1)∧(Si==Sj)
当然这个式子成立肯定有边界条件,当j-i为0，1，2的情况，如下
> P(i,i)=1
> P(i,i+1)=(Si==Si+1)
> P(i,i+2)=(Si==Si+2)
根据这个思路，我们就可以完成动态规划了，最终的答案即为所有 P(i, j) = 1P中 j-i+1（即子串长度）的最大值。注意：在状态转移方程中，我们是从长度较短的字符串向长度较长的字符串进行转移的，因此一定要注意动态规划的循环顺序。
程序实现
1.定义状态表
string s = "hello world!!!";
int n = s.size();
vector<vector <int>>obj(n,vector <int>(n,0));//创建一个向量存储容器 int
2.初始化状态表
//动态规划初始化 初始化对角线上的元素为1
for(int i=0;i<n;++i){
obj[i][i]=1;
}
3.实现状态转移方程
if(s[i]==s[j]&&obj[i+1][j-1]){//状态转移方程
obj[i][j]=1;
}
4.边界条件
int c = j-i;//i,j距离差用于分界
if(c<=2){
if(s[i]==s[j])
obj[i][j]=1;
}
5.记录最长的字符串
int max_len = 1;
int start_i = 1;
if(c+1>max_len&&obj[i][j]==1){
max_len = c+1;
start_i=i;
}
6.总代码
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
int max_len = 1;
int start_i = 1;
if(n<=1)
return s;
vector<vector <int>>obj(n,vector <int>(n,0));//创建一个向量存储容器 int
//动态规划初始化 初始化对角线上的元素为1
for(int i=0;i<n;++i){
obj[i][i]=1;
}
//动态规划转移方程实现
for(int j=1;j<n;++j)
{
for(int i=0;i<j;++i)
{
int c = j-i;//i,j距离差用于分界
if(c<=2){
if(s[i]==s[j])
obj[i][j]=1;
}
else{
if(s[i]==s[j]&&obj[i+1][j-1]){//状态转移方程
obj[i][j]=1;
}
}
if(c+1>max_len&&obj[i][j]==1){
max_len = c+1;
start_i=i;
}
}
}
string result = s.substr(start_i,max_len);
return result;
}
};
优化动态规划
1、去掉初始化
根据后续的代码可以看到，根本用不到对角线上的元素，所以根本不需要初始化
2、针对状态表最后一列的小优化
if(c+1>max_le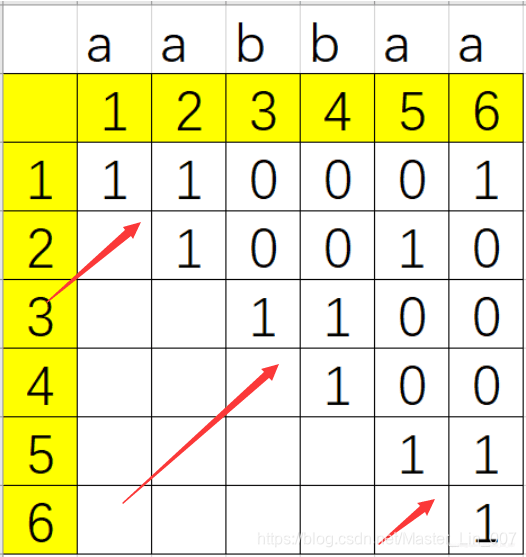
n&&obj[i][j]==1){
max_len = c+1;
if(max_len==n)
return s;
start_i=i;
}
3、从状态表发现规律如下
状态表中为1的点（除了对角线初始化的值）都是沿着右上方延伸过去的，延伸一次回文长度加2，并且，字符串中出现最大值的可能是从如图所示第二个箭头处开始的，因此我们可以选择先遍历中间位置，再从中间扩散。
class Solution {
public:
typedef struct tr_ret
{
int i;
int j;
}tr_ret;
tr_ret dig_traverse(string s,int n,int i,int j)//对角递归遍历
{
if(i>=n||j>=n||i<0||j<0)//递归边界
{
tr_ret temp;
temp.i = i+1;
temp.j = j-1;
return temp;
}
if(s[i]!=s[j])
{
tr_ret temp;
temp.i = i+1;
temp.j = j-1;
return temp;
}
return dig_traverse(s,n,i-1,j+1);
}
string longestPalindrome(string s) {int n = s.size();
int max_len = 1;
int start_i = 0;
int c;
tr_ret temp;
if(n<=1)
return s;
if(n%2==1)//奇数
{
int m = int(n/2);
int i = m-1;
int j = m+1;
temp = dig_traverse(s,n,i,j);
c = temp.j-temp.i+1;
if(c>max_len){
max_len = c;
start_i = temp.i;
}
while(1)
{
j--;
temp = dig_traverse(s,n,i,j);
c = temp.j-temp.i+1;
if(c>max_len){
max_len = c;
start_i = temp.i;
}
temp = dig_traverse(s,n,n-j-1,n-i-1);
c = temp.j-temp.i+1;
if(c>max_len){
max_len = c;
start_i = temp.i;
}
i--;
if(i<0)
break;
temp = dig_traverse(s,n,i,j);
c = temp.j-temp.i+1;
if(c>max_len){
max_len = c;
start_i = temp.i;
}
temp = dig_traverse(s,n,n-j-1,n-i-1);
c = temp.j-temp.i+1;
if(c>max_len){
max_len = c;
start_i = temp.i;
}
}
}
else//偶数
{
int m = int(n/2);
int i = m-1;
int j = m;
temp = dig_traverse(s,n,i,j);
c = temp.j-temp.i+1;
if(c>max_len){
max_len = c;
start_i = temp.i;
}
while(1)
{
i--;
if(i<0)
break;
temp = dig_traverse(s,n,i,j);
c = temp.j-temp.i+1;
if(c>max_len){
max_len = c;
start_i = temp.i;
}
temp = dig_traverse(s,n,n-j-1,n-i-1);
c = temp.j-temp.i+1;
if(c>max_len){
max_len = c;
start_i = temp.i;
}
j--;
temp = dig_traverse(s,n,i,j);
c = temp.j-temp.i+1;
if(c>max_len){
max_len = c;
start_i = temp.i;
}
temp = dig_traverse(s,n,n-j-1,n-i-1);
c = temp.j-temp.i+1;
if(c>max_len){
max_len = c;
start_i = temp.i;
}
}
}
string result = s.substr(start_i,max_len);
return result;
}
};
最后的优化仅仅是我自己的一个小小的思路，事实证明效率并不高。
我是杰出的小茄子，一个菜但是努力的人。
扫一扫
1969
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
