吴恩达机器学习笔记（一）

1 介绍

1.2 机器学习是什么？

Tom定义的机器学习：一个程序被认为能从经验E中学习，解决任务T，达到性能度量值P，当且仅当，有了经验E后，经过P评判，程序在处理T时的性能有所提升。

在目前存在的几种不同类型的学习算法中，主要的两种类型被我们称之为监督学习和无监督学习。

监督学习：我们将教计算机如何去完成任务

无监督学习：我们打算让计算机自己学习。

1.3监督学习

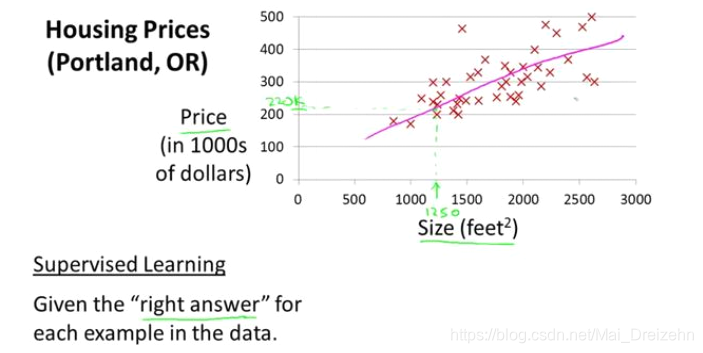
eg：房价问题（回归问题），肿瘤例子（分类问题）

我们每个数据集中的样本都有相应的“正确答案”

1.4无监督学习

eg：谷歌新闻，基因分类（聚类问题）

仅仅是一个数据集，让我们自己找它的“数据结构”

鸡尾酒宴问题（声音的分离）

2 单变量线性回归

2.1 模型标识

eg：预测住房价格

训练集如下：

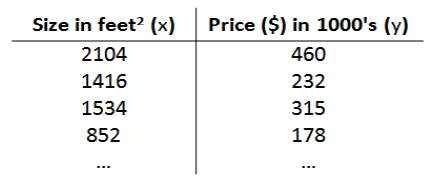
我们将要用来描述这个回归问题的标记如下：

m 代表训练集中实例的数量 x 代表特征/输入变量 y 代表目标变量/输出变量 （x，y）代表训练集 （x^(i)，y^(i)）代表第i个观察实例

h代表学习算法的解决方案或函数，成为假设

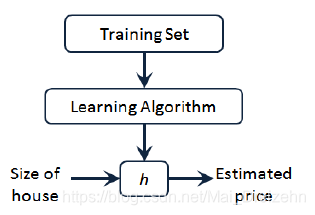
2.2代价函数

我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度。我们的目标要选择出可以使得建模误差的平方和最小的模型参数。即代价函数最小：

等高线图：

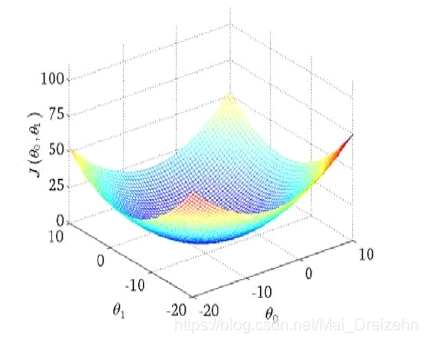
2.3/2.4代价函数的直观理解 

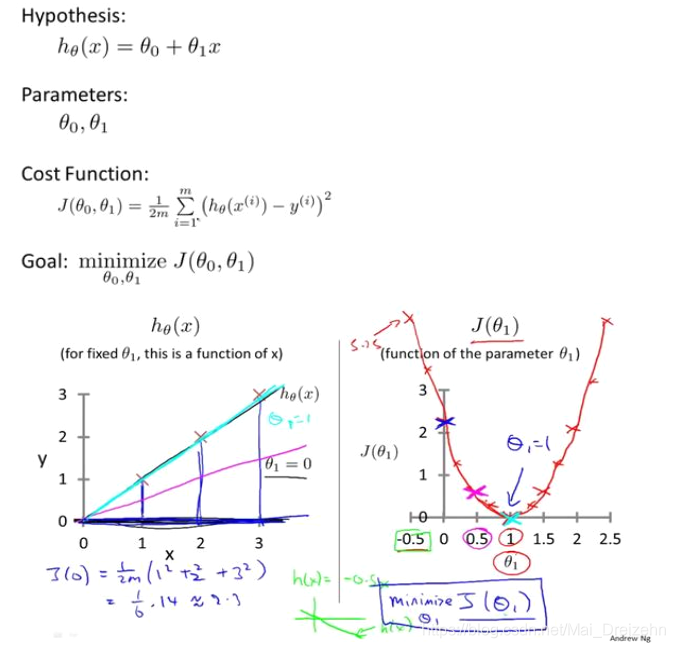
2.5梯度下降

梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数的最小值。

思想：寻找局部最小值，选择不同的初始参数组合可能会找到不同的局部最小值

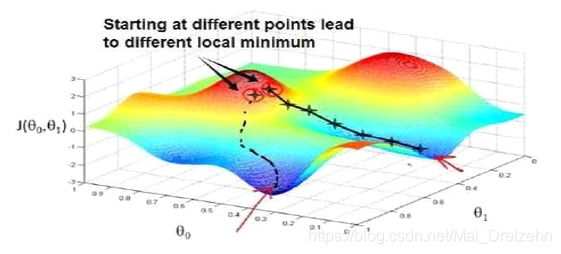
批量梯度下降（batch gradient descent）算法公式为：

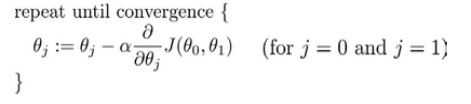
a是学习率，它决定了我们沿着能让代价函数下降程度最大的方向向下卖出的步子多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。

注意！！同时更新两个参数

2.6 梯度下降的直观理解

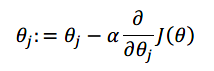
描述：对θ赋值，使得J（θ）按梯度下降最快方向进行，一直迭代，最终得到局部最小值。其中α是学习率，决定了我们能迈多大步子。

α过小，速度太慢，α太大，可能无法收敛。

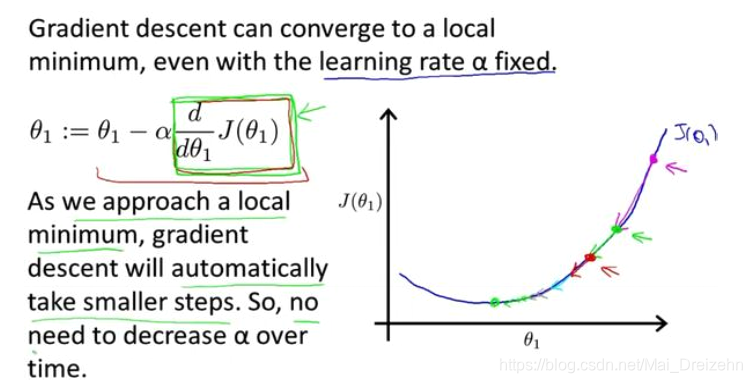
如图所示，从红色点开始，导数在一点一点变小，越来越平缓。

2.7 梯度下降的线性回归

梯度下降算法和线性回归算法比较如图：

求出代价函数的导数：Tips：h函数展开。

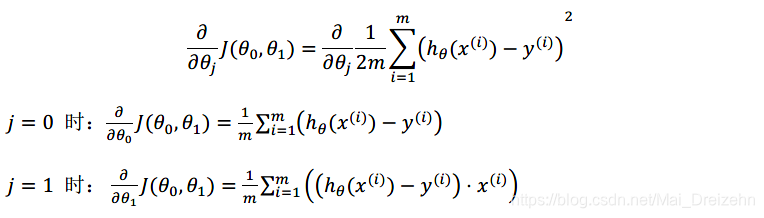
则算法改成：

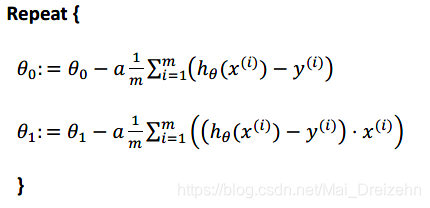
4 多变量线性回归

4.1多维特征

之前，我们讨论的是单变量的回归模型，现在我们对房价模型增加更多的特征。构成一个含有多个变量的模型，模型中的特征为（x1,x2,,,,,,,,xn）

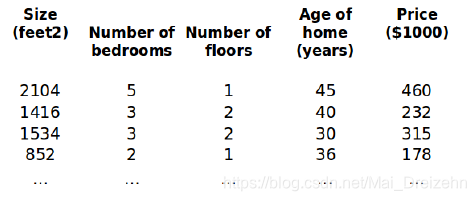
注释：

n  代表特征的数量

x^(i)  代表第i个训练实例，是特征矩阵的第i行，是一个向量

x^(i)_j  第i个训练实例的第j个特征

4.2 多变量梯度下降

构建代价函数：，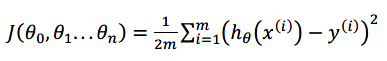

多变量线性回归的批量梯度下降算法为：

4.3 梯度下降法实践 - 特征缩放

我们尝试将所有特征的尺度都尽量缩放到-1 到 1之间

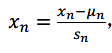
其中μn是平均值，Sn是标准差。

4.4 梯度下降法实践 - 学习率

4.5特征和多项式回归

线性回归并不适用于所有数据，有时我们需要曲线来适应我们的数据，

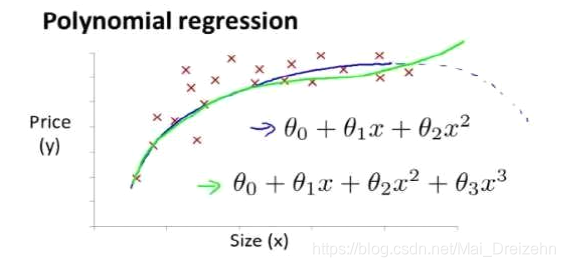
通常我们先观察再决定尝试怎样的模型。

我们可以令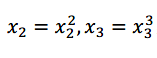，从而将模型转化为线性回归模型。

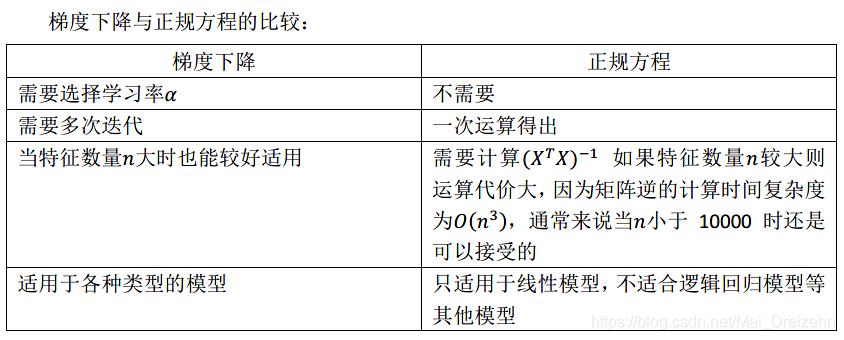
4.6 正规方程

其实对于某些线性回归问题，正规方程方法是更好的解决方案。

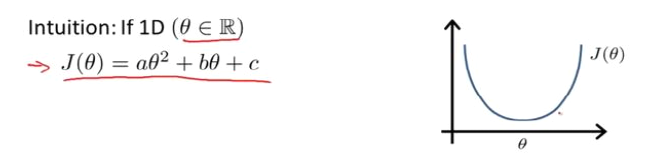
正规方程是通过求解下面的方程来找出使得代价函数最小得参数的：

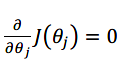
假设我们的训练集特征矩阵为X(包括了x0=1)，且我们的训练集结果为向量y，则利用正规方程解出向量

6 逻辑回归

6.2 假说表示

逻辑回归，该模型的输出变量范围始终在0和1之间。逻辑回归模型的假设是：

其中：X代表特征向量，g代表逻辑函数，公式为：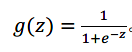

函数图像为：

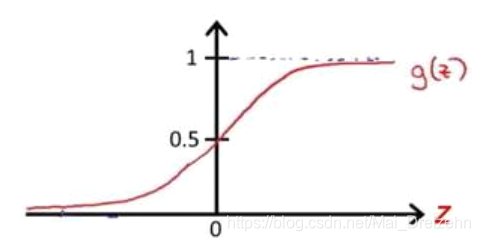
h(x)的作用是，对于给定的输入变量，根据选择的参数计算输出变量=1 的可能性，即

eg ，则表示有70% y为正向类。

6.3判定边界

假设我们现在有一个模型

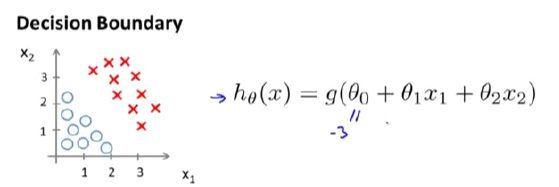
参数θ是向量[-3 1 1]。（类似线性规划）

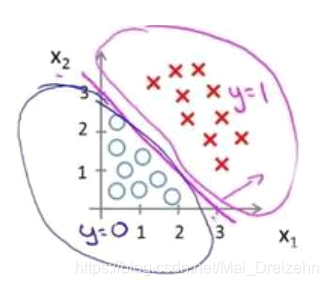
若模型如下：

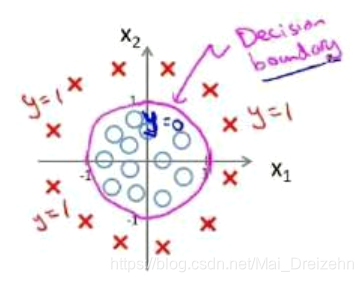
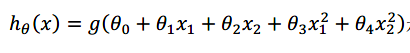
参数θ是[-1 0 0 1 1]

6.4 代价函数

对于线性回归模型，我们定义的代价函数是所有模型误差的平方和。若我们逻辑回归模型沿用这个定义，我们得到的代价函数是一个非凸函数

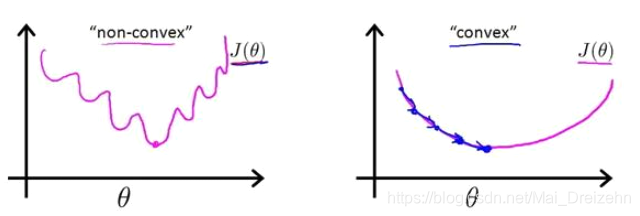
我们重新定义逻辑回归的代价函数为：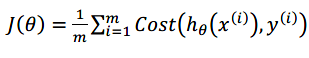

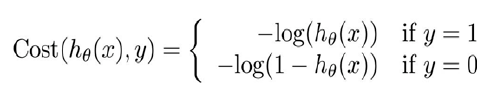
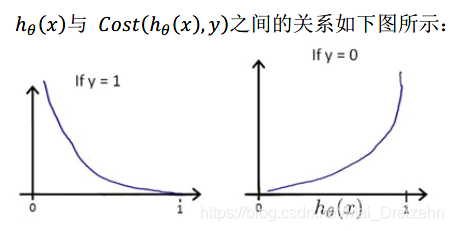
这样构建代价函数的特点是：当实际的y = 1 且h（x）也为1是，误差为0，当y = 1但h（x）不为1时误差随着h（x）变小而变大。

将代价函数简化：

 

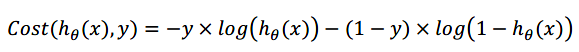
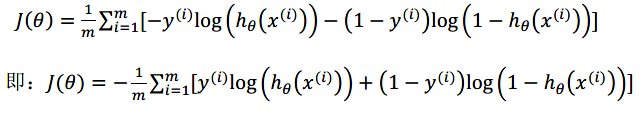
6.6高级优化

梯度下降并不是唯一的方法，还有一些其他优化代价函数的不同方法，共轭梯度法  BFGS（变尺度法）和L-BFGS（限制变尺度法）

6.7 多类别分类：一对多

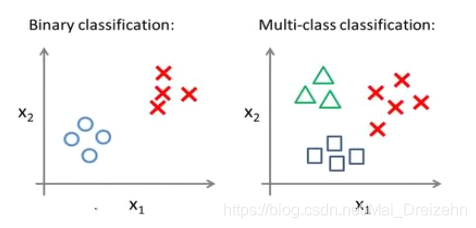
一对多，也称一对余

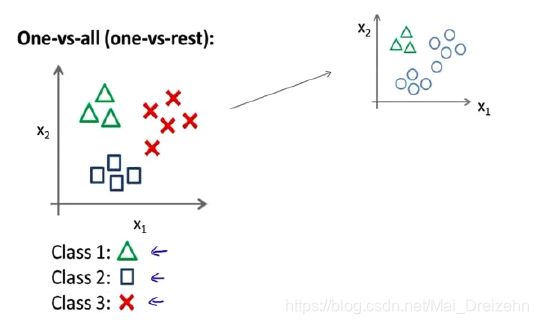
我们将多个类中的一个类标记为正向类（y = 1），然后将其他所有类都标记为负向类。

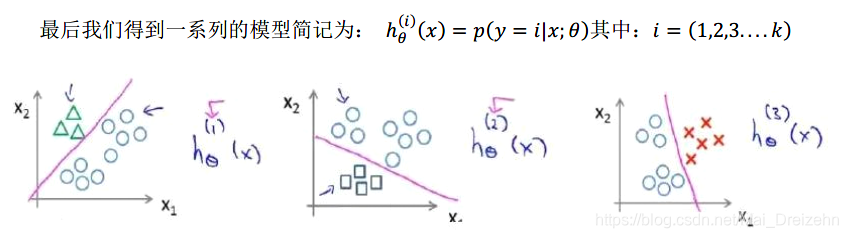
最后，在我们需要做预测时，我们将所有的分类机都运行一遍，然后对每一个输入变量，都选择最高可能性的输出变量