图-最短路径-Floyd

每一对顶点之间的最短路径

Floyd

• 时间复杂度：$O(n^3)$

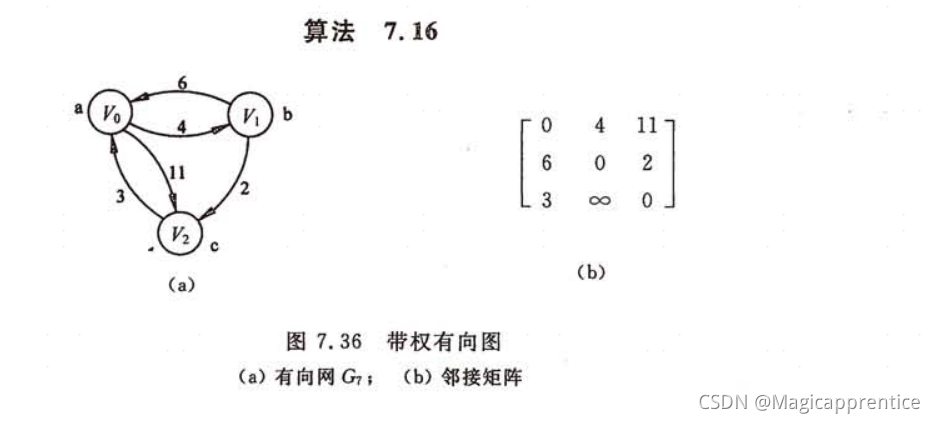
  弗洛伊德算法仍从图的带权邻接矩阵cost出发，其基本思想是：

  假设求从顶点$v_i$到$v_j$的最短路径:

  ​ 如果从$v_i$到$v_j$有弧，则从$v_i$到$v_j$存在一条长度为$arcs[i][j]$的路径，该路径不一定是最短路径，尚需进行n次试探。

  ​ 首先考虑路径$(v_i,v_o,v_j)$是否存在（即判别弧$(v_i,v_o)$和$(v_o,v_j)$是否存在）

  ​ 如果存在:则比较$(v_i,v_j)$和$(v_i,v_o,v_j)$的路径长度取长度较短者为从$v_i$到$v_j$的中间顶点的序号不大于0的最短路
  径。

  ​ 假如在路径上再增加一个顶点$v_1$,也就是说，如果$(v_i,...,v_1)$和$(v_1,...,v_j)$分别是当前找到的中间顶点的序号不大于0的最短路径，那么$(v_i,...,v_1,...,v_j)$就有可能是从$v_i$到$v_j$的中间顶点的序号不大于1的最短路径。

  ​ 将它和已经得到的从$v_i$到$v_j$中间顶点序号不大于0的最短路径相比较，从中选出中间顶点的序号不大于1的最短路径之后，再增加一个顶点$v_2$,继续进行试探。依次类推。

  ​ 在一般情况下，若$(v_i,...,v_k)$和$(v_k,...,v_j)$分别是从$v_i$到$v_k$和从$v_k$到$v_j$的中间顶点的序号不大于k-1的最短路径，则将$(v_i,...,v_k,...,v_j)$和已经得到的从 $v_i$到$v_j$​且中间顶点序号不大于k-1的最短路径相比较，其长度较短者便是从v:到v;的中间顶点的序号不大于k的最短路径。

  ​

  ​ 这样，在经过n次比较后，最后求得的必是从$v_i$到$v_j$的最短路径。按此方法，可以同时求得各对顶点间的最短路径。

  现定义一个n阶方阵序列$D^{(-1)},D^{(0)},D^{(1)},...,D^{(k)},...,D^{(n-1)}$
  其中

  ​ $D^{(-1)}[i][j]=G.arcs[i][j]$

  ​ $D^{(k)}[i][j]=Min\left\{D^{(k-1)}[i][j],D^{(k-1)}[i][k]+D^{(k-1)}[k][j]\right\}0\le K\le n-1$

  从上述计算公式可见，$D^{(1)}[i][j]$是从vi到vi的中间顶点的序号不大于1的最短路径的长度；$D^{(k)}[i][j]$是从vi到v;的中间顶点的序号不大于k的最短路径的长度；$D^{(n-1)}[i][j]$就是从vi到vi的最短路径的长度。
  由此可得Floyd算法。

  void ShortestPath FLOYD(MGraph G, PathMatrix &P[], DistancMatrix &D){
    //用Floyd算法求有向网G中各对顶点v和w之间的最短路径[v][w]及其
    //带权长度D[v][w]。若P[v][w][u]为TRUE,则u是从v到w当前求得最
    //短路径上的顶点。   
    for (v=0;v<G.vexnum; ++v) // 各对节点之间初始已知路径及距离
        for (w=0; w< G.vexnum; ++w) {
            D[v][w] = G.arcs[v][w]; // 初始时边的距离
            for (u=0; u< G.vexnum; ++u) P[v][w][u] = FALSE; //默认最短路径上的顶点都置为FALSE
            if (D[v][w] < INFINITY){ // 从v 到w有直接路径
                P[v][w][v] = True; P[v][w][w] = TRUE; //有直接路径的置为TRUE
            }//if
        }//for
    for (u = 0; u< G.vexnum; ++u)// 定义的k 序号不大于k的最短路径的长度
        for (v=0;v<G.vexnum; ++v)
            for (w = 0; w<G.vexnum;++w)
                if (D[v][u]+D[u][w]<D[v][w]){ // 从v经u到w的一条路径更短
                    D[v][w] = D[v][u]+D[u][w];
                    for (i = 0; i < G.vexnum; ++i)
                        P[v][w][i] = P[v][u][i] || P[u][w][i];
                }// if
  }// ShortestPath FLOYD
  

参考

• [数据结构(C语言版)].严蔚敏