Hdu 2256 Problem of Precision

精确问题求解

最新推荐文章于 2019-02-18 22:02:15 发布

原创最新推荐文章于 2019-02-18 22:02:15 发布 · 625 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#matrix #input #output #each #integer #fun

ACM/矩阵专栏收录该内容

4 篇文章

订阅专栏

本文介绍了一个涉及浮点数运算精度的编程挑战问题及其解决方案。该问题需要通过矩阵快速幂的方法来解决，避免使用快速幂+fmod的方式以克服浮点数精度损失的问题。文章详细解释了解题思路，并提供了一段具体的C语言实现代码。

Problem of Precision

Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 614 Accepted Submission(s): 344

Problem Description

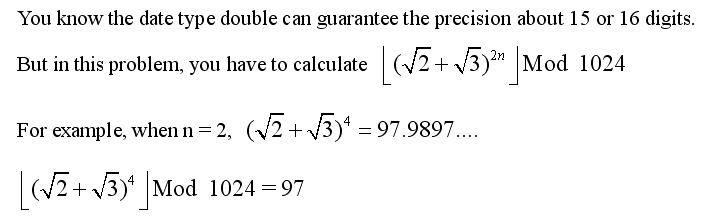
Input

The first line of input gives the number of cases, T. T test cases follow, each on a separate line. Each test case contains one positive integer n. (1 <= n <= 10^9)

Output

For each input case, you should output the answer in one line.

Sample Input

Sample Output

Source

HDOJ 2008 Summer Exercise（4）- Buffet Dinner

Recommend

lcy

参考别人的解题思路,写的代码，感觉他的解题思路写的很清晰。下面便是他的解题思路：
解题思路原文
这个题目用快速幂+fmod是AC不了的，应该是浮点数精度的原因，推导的过程都体现在图上了，剩下的工作就是二分矩阵求解了。

此外，在计算完x[n]和y[n]之后不能直接用(x[n]+(int)(y[n]*sqrt(6.0)))24来得到最后的结果的，先取整再模和先模再取整的结果是不一样的这一点举个例子就比较容易看出来了。

比如(2000*1.372)00，这样先乘再取模得到的结果就是744，如果先把2000模1000，显然最后结果就是0了。

#include<stdio.h>

int Matrix[3][3];
int tmp1[3][3],tmp2[3][3];

void fun(int n)                         //求矩阵的快速幂
{
    int i,j,k;
    n-=2;
    Matrix[1][1]=tmp1[1][1]=5;
    Matrix[1][2]=tmp1[1][2]=12;
    Matrix[2][1]=tmp1[2][1]=2;
    Matrix[2][2]=tmp1[2][2]=5;
    while(n)
    {
        if(n%2)
        {
            for(i=1;i<=2;i++)
                for(j=1;j<=2;j++)
                    tmp2[i][j]=Matrix[i][j];
            for(i=1;i<=2;i++)
                for(j=1;j<=2;j++)
                {
                    Matrix[i][j]=0;
                    for(k=1;k<=2;k++)
                        Matrix[i][j]=(Matrix[i][j]+tmp1[i][k]*tmp2[k][j])24;
                }
        }
        n/=2;
        for(i=1;i<=2;i++)
            for(j=1;j<=2;j++)
                tmp2[i][j]=tmp1[i][j];
        for(i=1;i<=2;i++)
            for(j=1;j<=2;j++)
            {
                tmp1[i][j]=0;
                for(k=1;k<=2;k++)
                    tmp1[i][j]=(tmp1[i][j]+tmp2[i][k]*tmp2[k][j])24;
            }
    }
}

int main(void)
{
    int T,n;
//    freopen("d:\\in.txt","r",stdin);
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        fun(n);
        if(n==1)                                         //n==1属于特殊情况
            printf("9\n");
        else
            printf("%d\n",(2 * (Matrix[1][1]*5+Matrix[1][2]*2 )-1)24);

    }
    return 0;
}