【力扣4行代码解题】572另一棵树的子树 | C++

总结：本题可以使用递归和迭代法，但平时还是建议两种方法都掌握，感兴趣的同学可以看看原题。

1 题目

力扣链接 ==> 572.另一棵树的子树
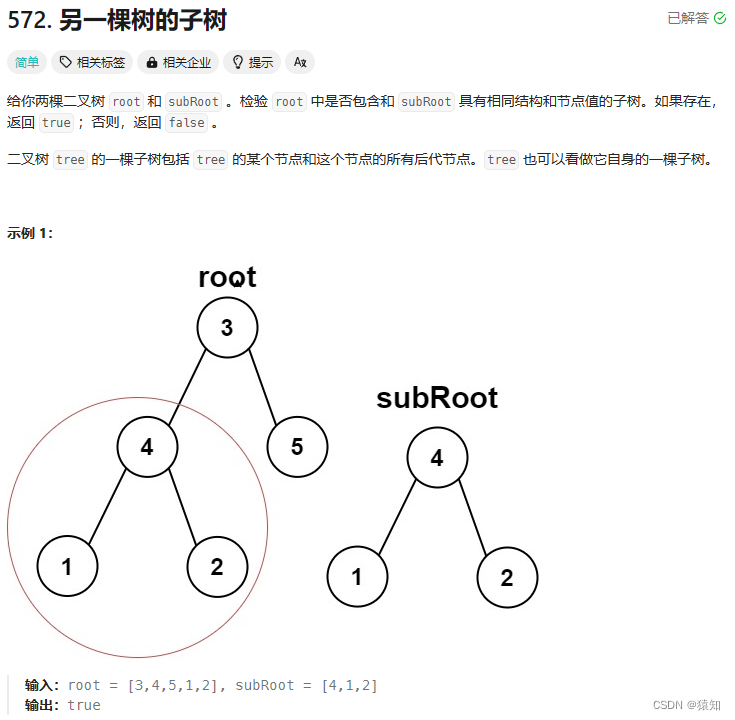
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

2 知识点

二叉树、深度优先搜索

3 代码及解释

class Solution {
public:
    bool compare(TreeNode* p, TreeNode* q) {
        if (!p || !q) return p == q;
        return p->val == q->val && compare(p->left, q->left) && compare(p->right, q->right);
    }

    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if (!root) return false;
        return compare(root, subRoot) || isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
    }
};

compare函数 的作用是对比两棵树是否相同：
第一行：处理两棵树存在某一为空或者二者都为空的情况（都为空自然是true）；
第二行：既然排除了两棵树存在空树的情况，那么剩下的一种就是两棵树都不为空，这个时候直接比较值，值相同则说明根节点一样，继续比较子节点，这里使用递归比较。

isSubtree函数 的作用是递归被查树的各个节点：
第一行：如果节点为空，那也就没有和subRoot比较的必要了；
第二行：比较两棵树的各个节点，如果不一致，就去左右子树继续比较。
由于是（|| ）或的关系，所以只要有任意一个子树满足条件都结束执行。

能力有限，不当之处，欢迎批评指正！