洛谷 P2184 贪婪大陆

链接

题意

长度为n的防线，你可以在一个区间[l, r]中放一种地雷，m次操作和询问，1表示在[l, r]中添加一种地雷，2表示查询[l, r]中的地雷种数

思路

最开始想了一下，就觉得是个简单的区间修改，然后把线段树模板敲了上去，发现不对，但是题意就是这个呀，后面发现题读错了，最开始以为是区间内的每个点都会添加一个地雷，后面仔细读才发现是这个区间类只添加一种地雷，是叫你求这个区间内的地雷种数。
其实不用线段数了，用先段数敲太多东西了，直接用树状数组，两个树状数组，这里来说一下，两个树状数组具体维护的是什么：
这里我们按照题目中给的样例画个图：

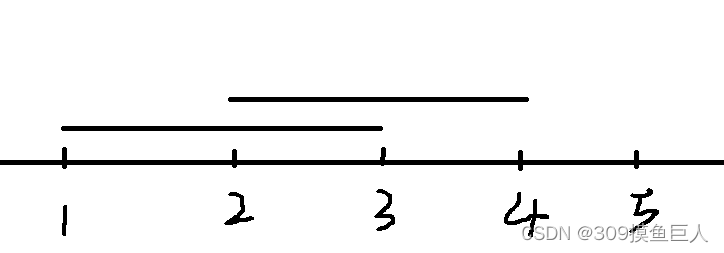
首先第一次查询问的是[2, 5]，这里发现就只有第一次插入的时候[2, 3]区间内有一种，第二次查询是[3, 5]，那么就是第一插入的[2, 3]和第二次插入的[3, 4]，一共两种，那么这个和前缀和很相似，前缀和我们自然而然就想到了树状数组，那么第一个树状数组我们维护的是以x为区间左端点开始的地雷种数，第二个梳妆数组维护的是以y为右端点的地雷种数。最后在求的时候直接相减即可。

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

int n, m;
int tr_1[N], tr_2[N];

int lowbit(int x) { return x & -x; }

void add(int x, int tr[]) { for (int i = x; i <= n; i += lowbit(i)) tr[i] += 1; }

int sum(int x, int tr[])
{
    int ans = 0;
    for (int i = x; i; i -= lowbit(i)) ans += tr[i];
    return ans;
}

void solve()
{
    cin >> n >> m;

    int op, l, r;
    while (m --)
    {
        cin >> op >> l >> r;
        if (op == 1) { add(l, tr_1), add(r, tr_2); }
        else
        {
            int ans = sum(r, tr_1) - sum(l - 1, tr_2);
            cout << ans << endl;
        }
    }
}

int main()
{
    std::ios::sync_with_stdio(false);

    solve();

    return 0;
}

补充一下，后面我想了一下，可不可以只用一个树状数组来计算（应该可以吧，只是我太菜了，实在没想到），我认为是不行的，因为我们在添加的时候，如果只有一个树状数组的话，我们可以想到在添加的时候就是：add(l, 1), add(r + 1, -1)，那么这样就可以保证就只是[l, r]之间的+1，然后在查询的时候直接是sum( r ) - sum(l - 1)，这样就表示了[l, r]之间的地雷种数了，如果是这样的话，我们会将有些区间里的地雷数减少，因为我们有一个add(r + 1, -1)，如果我们有一个区间的r恰好包含了之前的r + 1，那么这个时候区间内的地雷数就是减少了的。所以我们要用两个梳妆数组，一个表示起点，一个表示终点，终点之后的点肯定包含了这个点的，起点之前的点也可定是包含了这个点的。我们后面在找的时候，是以r为起点的数量减去以l - 1为终点的数量。