计算机网络中的编码与校验技术详解-优快云博客

本文链接：https://blog.youkuaiyun.com/MadeAndCreate/article/details/126218828

本文详细介绍了计算机网络中几种重要的编码技术，包括8421码、余3码和2421码的原理和应用。此外，还深入探讨了ASCII码的使用范围，以及奇偶校验码的工作机制，展示了奇校验码和偶校验码的计算过程。接着，重点讲解了海明码的构造、检错和纠错能力，通过实例解析了如何确定校验位和进行错误检测。最后，提到了循环冗余校验码（CRC）的生成和其在错误检测中的作用。这些编码和校验方法对于确保数据传输的准确性和可靠性至关重要。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

计算机网络

### BCD码

8421码

8421码（有权码）的映射关系:

0	1	2	3	4	5	6	7	8	9
0000	0001	0010	0011	0100	0101	0110	0111	1000	1001

例题1：1+3=4 -> 0001 + 0011 = 0100
例题2：5+8=13 -> 原：0101 + 1000 =1101 修正过程：1101 + 0110 = 0001 0011
相加后不在映射表内，则需要在原结果后在加上0110
例题3：在计算机中的保存形式985：1001 1000 0101

余3码

余3码：8421码+（0011）无权吗

0	1	2	3	4	5	6	7	8	9
0011	0100	0101	0110	0111	1000	1001	1010	1011	1100

2421码

0	1	2	3	4	5	6	7	8	9
0000	0001	0010	0011	0100	1011	1100	1101	1110	1111

【注】2421码规定在5（1011）及以后的数字首位一定是1

ASCII码

1. 可印刷的字符：32~126，其余为控制字符
2. 大写字母：65（0100 0001） ~ 90（0101 1010）小写字母：97~122

奇偶校验

检验原理简介

信息	A	B	C	D
编码	00	01	10	11
2bit映射到4个合法状态

信息	A	B	C	D
编码	100	001	010	111
3bit映射到4个合法状态 (有4个冗余的非法状态)

1. 由若干位代码组成的字叫<mark>码字</mark>。    
2. 将两个码字逐位对比，具有不同的位的个数称为<mark>两个码字间的距离</mark>。  
3. 一种编码方案可能有若干个合法码字，各合法码字间的最小距离称为“<mark>码距</mark>”。
4. 当（码距）d=1时，无检错的能力；当d=2时，有检错的能力；当d=3时，若设计合理，可能有检错、纠错能力

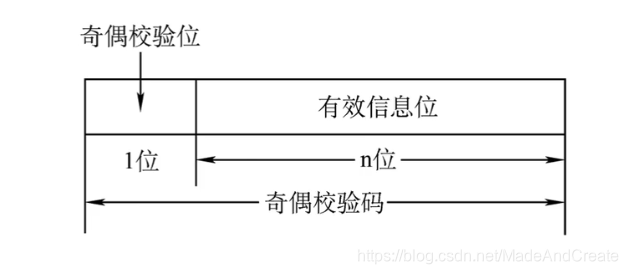
奇偶校验码

1. 奇校验码：整个校验码（有效信息位数和校验位）中“1”的个数为奇数。
2. 偶校验码：整个校验码（有效信息位数和校验位）中“1”的个数为偶数。  

![奇偶校验码](https://img-blog.csdnimg.cn/20210105221341860.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L01hZGVBbmRDcmVhdGU=,size_16,color_FFFFFF,t_70#pic_center)
【例题1】给出两个编码1001101和1010111的奇校验码和偶校验码。

设最高位为校验码，其余7位是信息位，则对应的奇偶校验码：

奇校验码：11001101 01010111

3. 偶校验的硬件实现：各信息进行异或运算（模2加）运算，得到的结果即为偶校验位
   - 异或运算：1⊕1=0；1⊕0=1（相同为1，不同为0）
   - 进行偶校验结果为为0这编码传输正确，结果为1说明错误
   - 奇偶校验只能检测出奇数个传输位的错误，若有偶数个传输位错误则不能检测数

海明校验码

海明码的设计思路简介

将信息位分组进行偶校验->多个校验位->多个校验位标注出错位置

【问题1】：一串编码n位需要多少个校验位？

信息位n位，需要k为校验位，k位校验码能表示2^k种状态

海明码求解步骤

【例题】信息位1010

确定海明码位数：2^k≥n+k+1

n=4–>k=3

设信息位D₄D₃D₂D₁，共4位，校验位为P₃P₂P₁，共3位，对应的海明码位H₇H₆H₅H₄H₃H₂H₁。

确定校验位分布

H₇	H₆	H₅	H₄	H₃	H₂	H₁
D₄	D₃	D₂	P₃	D₁	P₂	P₁
1	0	1		0

校验位P_i放在海明位号为2^i-1的位置上

信息位按顺序放在其余位置

求校验位
- 3.1将信息位所对应的海明码下标用二进制表示
  - H₃：011
  - H₅：101
  - H₆：110
  - H₇：111
- 3.2从左往右将同一列二进制分为一组
  - H₃：011–D₁
  - H₅：101–D₂
  - H₆：110–D₃
  - H₇：111–D₄
    
    列数1（D₁）数2（D₂）数3（D₃）数4（D₄）
    第一列 1 1 0 1
    第二列 1 0 1 1
    第三列 0 1 1 1
  表1
  
  信息位表
  D₁ D₂ D₃ D₄
  0 1 0 1

列	数1（D₁）	数2（D₂）	数3（D₃）	数4（D₄）
第一列	1	1	0	1
第二列	1	0	1	1
第三列	0	1	1	1

3.3将表1中每列中数为1所对应的信息位的值进行异或运算
- P₁ = D₁ ⨁ D₂ ⨁ D₄ = 0 ⨁1 ⨁ 1 = 0
  - P₂ = D₁ ⨁ D₃ ⨁ D₄ = 0 ⨁ 0 ⨁ 1 = 1
  - P₃ = D₂ ⨁ D₃ ⨁ D₄ = 1 ⨁ 0 ⨁ 1 = 0
H₇ H₆ H₅ H₄ H₃ H₂ H₁
D₄ D₃ D₂ P₃ D₁ P₂ P₁
1 0 1 0 0 1 0

检错纠错
- 将3.3中的运算式子加上对应的校验位进行异或运算,得到结果全为0说明信息无误
  - S₁ = P₁ ⨁ D₁ ⨁ D₂ ⨁ D₄ = 0 ⨁ 0 ⨁1 ⨁ 1 = 0
  - S₂ = P₂ ⨁ D₁ ⨁ D₃ ⨁ D₄ = 1 ⨁ 0 ⨁ 0 ⨁ 1 = 0
  - S₃ = P₃ ⨁ D₂ ⨁ D₃ ⨁ D₄ = 0 ⨁ 1 ⨁ 0 ⨁ 1 = 0
  接收到的的信息：1010010
- 如果得到的信息有去一位不为0
  
  【例】接收到的信息为：1010000
  - S₁ = P₁ ⨁ D₁ ⨁ D₂ ⨁ D₄ = 0 ⨁ 0 ⨁1 ⨁ 1 = 0
  - S₂ = P₂ ⨁ D₁ ⨁ D₃ ⨁ D₄ = 0 ⨁ 0 ⨁ 0 ⨁ 1 = 1
  - S₃ = P₃ ⨁ D₂ ⨁ D₃ ⨁ D₄ = 0 ⨁ 1 ⨁ 0 ⨁ 1 = 0
    
    从S₃到S₁的结果连接起来的：010 (2)，组成的二进制指明海明码的第2位H₂出现错误
海明码检错、纠错能力
- 检错能力——2位
- 纠错能力——1位

加上“全校验码”的海明码

H₈	H₇	H₆	H₅	H₄	H₃	H₂	H₁
P_全	D₄	D₃	D₂	P₃	D₁	P₂	P₁
1	1	0	1	0	0	1	0

全校验码：通过所有海明码的值进行偶校验得到全校验位的值
- H₈ = 0 ⨁ H₇ ⨁ H₆ ⨁ H₅ ⨁ H₄ ⨁ H₃ ⨁ H₂ ⨁ H₁
- H₈ ⨁ H₇ ⨁ H₆ ⨁ H₅ ⨁ H₄ ⨁ H₃ ⨁ H₂ ⨁ H₁ = 0
校验方程：
- S₁ = P₁ ⨁ D₁ ⨁ D₂ ⨁ D₄ = 0 ⨁ 0 ⨁1 ⨁ 1 = 0
- S₂ = P₂ ⨁ D₁ ⨁ D₃ ⨁ D₄ = 1 ⨁ 0 ⨁ 0 ⨁ 1 = 0
- S₃ = P₃ ⨁ D₂ ⨁ D₃ ⨁ D₄ = 0 ⨁ 1 ⨁ 0 ⨁ 1 = 0
  - S₃S₂S₁ = 000且全体偶校验成功 ->无错误
  - S₃S₂S₁ ≠ 000且全体偶校验失败->有1位错误，纠正即可
  - S₃S₂S₁ ≠ 000且全体偶校验成功 ->有2位错误，需重传

循环冗余验证码

循环冗余校验码的基本思想：

循环冗余校验码

发送方和接收方约定一个“除数”
K个信息位+R位校验位作为“被除数”，添加校验位后需保证除法的余数为0
收到信息后，进行除法检查余数是否为0
若余数非0说明出错，则进行重传或者纠错

【例题】设生成多项式位G(x) = x³ + x² + 1，信息码101001对应的的CRC码。

确定K、R以及多项式对应的二进制码
- K = 信息码的长度 = 6
- R = 生成多项式的最高次幂 = 3
- ->校验码位数N = K + R = 9
- 生成多项式G(x) = x³ + x ² + 1 = 1 * x³ + 1 * x² + 0 * x¹ + 1 * x⁰，对应的二进制码：1101
移位
- 信息码左移R位，低位补0
相除
- 对移位后的信息码，用多项式进行模2除，产生余数。