二分检索
分治法的思想就是把整个问题分成若干个小问题后分而治之。
①通常情况下,子问题与原问题具有相同的类型。
②可以反复使用分治策略,直到可以直接求解子问题为止。
③适合采用递归过程来表示。
题解:
在一个有序数组中查找元素,采用二分查找。找到数组的中间位置的元素a[(low+high)/2],如果要找的元素比它大,则把low更新为(low+high)/2+1;
如果要找的元素比它小,则把high更新为(low+high)/2-1;直到检索到该元素或low>high时检索失败为止。
代码:
#include<iostream>
using namespace std;
void find(int a[],int n,int x,int &index)
{
int i;
int low=1;
int high=n;
while(low<=high)
{
int mid=(low+high)/2;
if(x<a[mid])
{
high=mid-1;
}
else if(x>a[mid])
{
low=mid+1;
}
else
{
index=mid;
return ;
}
}
}
int main()
{
int a[10],i,index=-1,x,n;
cout<<"请输入数组有多少个元素"<<endl;
cin>>n;
cout<<"请输入有序的数列"<<endl;
for(i=0;i<n;i++)
{
cin>>a[i];
}
cout<<"请输入你要找的元素"<<endl;
cin>>x;
find(a,n,x,index);
cout<<"它的下标为:"<<index<<endl;
return 0;
}
}
输出示例:
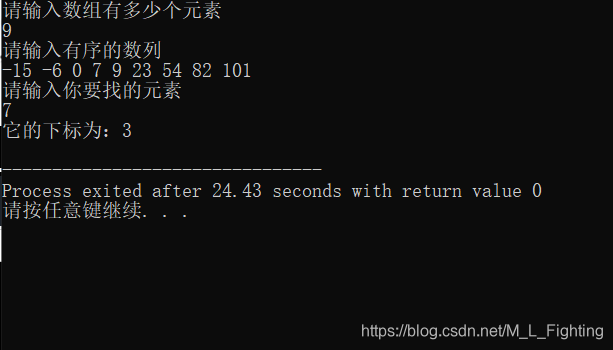





 本文深入讲解了二分检索算法,一种高效的在有序数组中查找特定元素的方法。文章详细阐述了分治法思想,通过不断缩小搜索范围实现快速定位,直至找到目标元素或确认不存在。附带的C++代码示例清晰展示了二分检索的实现过程。
本文深入讲解了二分检索算法,一种高效的在有序数组中查找特定元素的方法。文章详细阐述了分治法思想,通过不断缩小搜索范围实现快速定位,直至找到目标元素或确认不存在。附带的C++代码示例清晰展示了二分检索的实现过程。
















 1347
1347

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








