Datawhale X 李宏毅苹果书 AI夏令营 - 跟李宏毅学深度学习(入门)

《深度学习详解》主要内容源于《机器学习》（2021年春），选取了《机器学习》（2017年春） 的部分内容，在这些基础上进行了一定的原创，补充了不少除这门公开课之外的深度学习相关知识。

为了尽可能地降低阅读门槛，笔者对这门公开课的精华内容进行选取并优化，对所涉及的公式都给出详细的推导过程，对较难理解的知识点进行了重点讲解和强化，以方便读者较为轻松地入门。

在理论严谨的基础上，本书保留了公开课中大量生动有趣的例子，帮助读者从生活化的角度理解深度学习的概念、建模过程和核心算法细节，包括——

• 卷积神经网络、Transformer、生成模型、自监督学习（包括 BERT 和 GPT）等深度学习常见算法，
• 对抗攻击、领域自适应、强化学习、元学习、终身学习、网络压缩等深度学习相关进阶算法。

开源教程还获得了李宏毅老师的推荐~
链接指路：https://github.com/datawhalechina/leedl-tutorial（欢迎大家star~）

1、机器学习基础

	机器学习：让机器具备去寻找一个函数一个方法的概念。
	-- 机器学习存在不同的类别：回归、分类、结构化学习
	回归：如果机器学习要找的函数是一个数值、一个标量(scalar)， 这种学习的任务称为回归。
	分类：分类是让机器做选择题。人们设置好选项，让机器选择一个选项，对应的选项称之为类别，需要找的函数存在于设定好的分类中，这种任务
	称为分类。
	结构化学习：机器不仅仅只需要输出一个数值或选择一个类别，而是输出一个结构体，如：图像、文章等，这种任务称之为结构化学习。

案例分析

案例：通过已知的数据集来预测未来某个时间点的数据 ---- 预测明天视频点赞数（已知：过去每天的点赞数、浏览数、订阅数）

y = b + wx1

机器学习分三步分析：
1、写一个带有未知参数的函数；
2、定义因不确定因素造成的损失，可预测这个损失也是一个函数；
3、找出一个最优化的参数。使用梯度下降确定优化的方法。

y = b + wx1
模型：带有未知参数的函数；
特征：带有未知参数的函数中已知的信息参数(x1)；
权重：w称之为权重；
偏置：b称之为偏置；

估测的值y与实际值y间的差距，根据不同的算法，分为：平均绝对误差(MAE) 和 均方误差(MSE)。

交叉熵：一些任务中的 估测的值y与实际值y 是概率分布存在的， 此时会选择 交叉熵。
误差表面：调试不同参数计算损失所画出来的等高线，称之为误差表面。

内容分析

机器学习找函数的过程，分成 3 个步骤。第一个步骤是写出一个带有未知参数的函数 f，其能预测未来观看次数。比如将函数写成

  									y = b + wx1 

其中，y 是准备要预测的东西，要预测的是今天（2 月 26 日）这个频道总共观看的人，y 就假设是今天总共的观看次数。 x1是这个频道，前一天（2 月 25 日）总共的观看次数，y 跟 x1 都是数值，b 跟 w 是未知的参数，它是准备要通过数据去找出来的，
w 跟 b 是未知的，只是隐约地猜测。猜测往往来自于对这个问题本质上的了解，即领域知识（domain knowledge）。
机器学习就需要一些领域知识。这是一个猜测，也许今天的观看次数，总是会跟昨天的观看次数有点关联，所以把昨天的观看次数，
乘上一个数值， 但是总是不会一模一样，所以再加上一个 b 做修正，当作是对于 2 月 26 日，观看次数的预测，这是一个猜测，
它不一定是对的，等一下回头会再来修正这个猜测。总之，y = b + w ∗ x1，而 b 跟 w 是未知的。
带有未知的参数（parameter）的函数称为模型（model）。模型在机器学习里面，就是一个带有未知的参数的函数，
特征（feature） x1 是这个函数里面已知的，它是来自于后台的信息，2 月 25 日点击的总次数是已知的，而 w 跟 b
是未知的参数。 w 称为权重（weight），b 称为偏置（bias）。这个是第一个步骤。第 2
个步骤是定义损失（loss），损失也是一个函数。 这个函数的输入是模型里面的参数，模型是 y = b + w ∗ x1，而 b 跟 w
是未知的，损失是函数 L(b, w)，其输入是模型参数 b 跟w。
损失函数输出的值代表，现在如果把这一组未知的参数，设定某一个数值的时候，这笔数值好还是不好。 举一个具体的例子，假设未知的参数的设定是
b = 500，w = 1，预测未来的观看次数的函数就变成 y = 500 + x1。
要从训练数据来进行计算损失，在这个问题里面，训练数据是这一个频道过去的观看次数。 举个例子，从 2017 年 1 月 1 日到
2020 年 12 月 31 日的观看次数（此处的数字是随意生成的），接下来就可以计算损失。

把 2017 年 1 月 1 日的观看次数，代入这一个函数里面

  								yˆ = 500 + 1x1 

可以判断 b = 500，w = 1 的时候，这个函数有多棒。x1 代入 4800，预测隔天实际上的观看次数结果为 yˆ = 5300，真正的结果是 4900， 真实的值称为标签（label），它高估了这个频道可能的点击次数，可以计算一下估测的值 yˆ 跟真实值
y 的差距 e。 计算差距其实不只一种方式，比如取绝对值：

  								e1 = |y − yˆ| = 400

我们不是只能用 1 月 1 日，来预测 1 月 2 日的值，可以用 1 月 2 日的值，来预测 1 月 3日的值。根据 1 月 2
日的观看次数， 预测的 1 月 3 日的观看次数的，值是 5400。接下来计算5400 跟跟标签（7500）之间的差距，低估了这个频道。
在 1 月 3 日的时候的观看次数，才可以算出：

  								e2 = |y − yˆ| = 2100 	

我们可以算过这 3 年来，每一天的预测的误差，这 3 年来每一天的误差，通通都可以算出来，每一天的误差都可以得到 e。 接下来把每一天的误差，通通加起来取得平均，得到损失L

其中，N 代表训验数据的个数，即 3 年来的训练数据，就 365 乘以 3，计算出一个 L，，L 是每一笔训练数据的误差 e
相加以后的结果。L 越大，代表现在这一组参数越不好，L越小，代表现在这一组参数越好。估测的值跟实际的值之间的差距，其实有不同的计算方法，计算 y 与 yˆ 之间绝对值的差距，称为平均绝对误差（Mean Absolute Error，MAE）。

  	e = |yˆ − y| 

如果算 y 与 yˆ之间平方的差距，如式 (1.7) 所示，则称为均方误差（Mean SquaredError，MSE）。

  	e = (ˆy y −y)2

有一些任务中 y 和 yˆ 都是概率分布，这个时候可能会选择交叉熵（cross entropy），这个是机器学习的第
2步。刚才举的那些数字不是真正的例子，以下的数字是真实的例子，是这个频道真实的后台的数据，所计算出来的结果。可以调整不同的 w和不同b，求取各种w 和各种 b，组合起来以后，我们可以为不同的 w 跟 b 的组合，都去计算它的损失，就可以画出图 1.2所示的等高线图。在这个等高线图上面，越偏红色系，代表计算出来的损失越大，就代表这一组 w 跟 b越差。如果越偏蓝色系，就代表损失越小，就代表这一组 w 跟 b 越好，拿这一组 w 跟 b，放到函数里面，预测会越精准。假设 w = −0.25, b = −500，这代表这个频道每天看的人越来越少，而且损失这么大，跟真实的情况不太合。如果 w = 0.75, b = 500，估测会比较精准。如果 w 代一个很接近 1 的值，b 带一个小小的值，比如说 100多，这个时候估测是最精准的，这跟大家的预期可能是比较接近的，就是拿前一天的点击的总次数，去预测隔天的点击的总次数，可能前一天跟隔天的点击的总次数是差不多的，因此 w 设 1，b 设一个小一点的数值，也许估测就会蛮精准的。如图 1.2 所示的等高线图，就是试了不同的参数，计算它的损失，画出来的等高线图称为误差表面（error surface）。这是机器学习的第 2 步。

接下来进入机器学习的第 3 步：解一个最优化的问题。找一个 w 跟 b，把未知的参数找一个数值出来，看代哪一个数值进去可以让损失 L
的值最小，就是要找的 w 跟 b，这个可以让损失最小的 w 跟 b 称为 w∗ 跟 b∗ 代表它们是最好的一组 w 跟
b，可以让损失的值最小。梯度下降（gradient descent）是经常会使用优化的方法。为了要简化起见，先假设只有一个未知的参数 w，b
是已知的。w 代不同的数值的时候，就会得到不同的损失，这一条曲线就是误差表面，只是刚才在前一个例子里面，误差表面是 2
维的，这边只有一个参数，所以这个误差表面是 1 维的。怎么样找一个 w 让损失的值最小呢? 如图 1.3 所示，首先要随机选取一个初始的点
w0。接下来计算 ∂L∂w |w=w0，在 w 等于 w0 的时候，参数 w 对损失的微分。计算在这一个点，在 w0
这个位置的误差表面的切线斜率，也就是这一条蓝色的虚线，它的斜率，如果这一条虚线的斜率是负的，代表说左边比较高，右边比较低。在这个位置附近，左边比较高，右边比较低。如果左边比较高右边比较低的话，就把
w
的值变大，就可以让损失变小。如果算出来的斜率是正的，就代表左边比较低右边比较高。左边比较低右边比较高，如果左边比较低右边比较高的话，就代表把
w 变小了，w 往左边移，可以让损失的值变小。这个时候就应该把 w
的值变小。我们可以想像说有一个人站在这个地方，他左右环视一下，算微分就是左右环视，它会知道左边比较高还是右边比较高，看哪边比较低，它就往比较低的地方跨出一步。这一步的步伐的大小取决于两件事情：•
第一件事情是这个地方的斜率，斜率大步伐就跨大一点，斜率小步伐就跨小一点。• 另外，学习率（learning rate）η
也会影响步伐大小。学习率是自己设定的，如果 η 设大一点，每次参数更新就会量大，学习可能就比较快。如果 η
设小一点，参数更新就很慢，每次只会改变一点点参数的数值。这种在做机器学习，需要自己设定，不是机器自己找出来的，称为超参数（hyperparameter）。

• 第一件事情是这个地方的斜率，斜率大步伐就跨大一点，斜率小步伐就跨小一点。

• 另外，学习率（learning rate）η 也会影响步伐大小。学习率是自己设定的，如果 η 设大一点，每次参数更新就会量大，学习可能就比较快。如果 η
  设小一点，参数更新就很慢，每次只会改变一点点参数的数值。这种在做机器学习，需要自己设定，不是机器自己找出来的，称为超参数（hyperparameter）。

     Q: 为什么损失可以是负的?
     A: 损失函数是自己定义的，在刚才定义里面，损失就是估测的值跟正确的值的绝对值。
     如果根据刚才损失的定义，它不可能是负的。但是损失函数是自己决定的，比如设置一个损失函数为绝对值再减100，
     其可能就有负的。这个曲线并不是一个真实的损失，并不是一个真实任务的误差表面。因此这个损失的曲线可以是任何形状。
     把 w0 往右移一步，新的位置为 w1，这一步的步伐是 η 乘上微分的结果，即：
  

接下来反复进行刚才的操作，计算一下 w1 微分的结果，再决定现在要把 w1 移动多少，再移动到 w2，再继续反复做同样的操作，不断地移动 w 的位置，最后会停下来。往往有两种情况会停下来。

• 第一种情况是一开始会设定说，在调整参数的时候，在计算微分的时候，最多计算几次。上限可能会设为 100 万次，参数更新100万次后，就不再更新了，更新次数也是一个超参数。
• 还有另外一种理想上的，停下来的可能是，当不断调整参数，调整到一个地方，它的微分的值就是这一项，算出来正好是 0
  的时候，如果这一项正好算出来是 0，0 乘上学习率 η 还是 0，所以参数就不会再移动位置。假设是这个理想的情况，把 w0 更新到 w1，再更新到 w2，最后更新到 wT 有点卡，wT 卡住了，也就是算出来这个微分的值是 0 了，参数的位置就不会再更新。

梯度下降有一个很大的问题，没有找到真正最好的解，没有找到可以让损失最小的 w。在图 1.4 所示的例子里面，把 w
设定在最右侧红点附近这个地方可以让损失最小。但如果在梯度下降中，w0 是随机初始的位置，也很有可能走到 wT 这里，训练就停住了，无法再移动
w 的位置。右侧红点这个位置是真的可以让损失最小的地方，称为全局最小值（global minima），而 wT
这个地方称为局部最小值（local minima），其左右两边都比这个地方的损失还要高一点，但是它不是整个误差表面上面的最低点。

所以常常可能会听到有人讲到梯度下降不是个好方法，这个方法会有局部最小值的问题，无法真的找到全局最小值。事实上局部最小值是一个假问题，在做梯度下降的时候，真正面对的难题不是局部最小值。有两个参数的情况下使用梯度下降，其实跟刚才一个参数没有什么不同。如果一个参数没有问题的话，可以很快的推广到两个参数。假设有两个参数，随机初始值为
w0, b0。要计算 w, b 跟损失的微分，计算在 w = w0 的位置，b = b0 的位置，要计算 w 对 L 的微分，计算 b 对 L 的微分

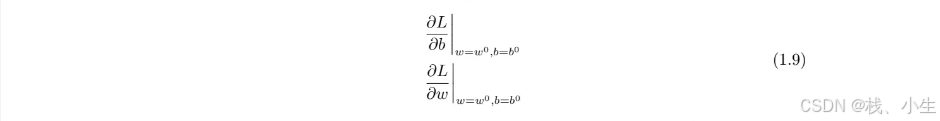
计算完后更新 w 跟 b，把 w0 减掉学习率乘上微分的结果得到 w1，把 b0 减掉学习率乘上微分的结果得到 b1。

在深度学习框架里面，比如 PyTorch 里面，算微分都是程序自动帮计算的。
就是反复同样的步骤，就不断的更新 w 跟 b，期待最后，可以找到一个最好的 w，w∗ 跟最好的 b∗. 如图 1.5 所示，随便选一个初始的值，先计算一下 w 对 L 的微分，跟计算一下 b 对 L 的微分，
接下来更新 w 跟 b，更新的方向就是 ∂L/∂w，乘以 η 再乘以一个负号，∂L/∂b，算出这个微分的值，就可以决定更新的方向，可以决定 w 要怎么更新。
把 w 跟 b 更新的方向结合起来，就是一个向量，就是红色的箭头，再计算一次微分，再决定要走什么样的方向，
把这个微分的值乘上学习率，再乘上负号，我们就知道红色的箭头要指向那里，就知道如何移动 w 跟 b 的位置，一直移动，期
待最后可以找出一组不错的 w, b。实际上真的用梯度下降，进行一番计算以后，这个是真正的数据，算出来的最好的 w∗ = 0.97, b∗ = 100，跟猜测蛮接近的。
因为x1 的值可能跟 y 很接近，所以这个 w 就设一个接近 1 的值，b 就设一个比较偏小的值。损失 L(w∗, b∗) 算一下是 480，也就是在 2017 到 2020 年的数据上，如果使用这一个函数，b 代100，w 代 0.97，平均的误差是 480，其预测的观看次数误差，大概是 500 人左右。

补充学习视频：
预测本频道观看人数（上） - 机器学习基本概念简介_哔哩哔哩_bilibili