递归模型

对递归的理解的要点主要在于放弃!

放弃你对于理解和跟踪递归全程的企图，只理解递归两层之间的交接，以及递归终结的条件。（知乎-Fireman A）

一、递归的定义

从前有座山，山里有座庙，庙里有个老和尚，正在给小和尚讲故事呢！故事是什么呢？“从前有座山，山里有座庙，庙里有个老和尚，正在给小和尚讲故事呢！故事是什么呢？‘从前有座山，山里有座庙，庙里有个老和尚，正在给小和尚讲故事呢！故事是什么呢？……’”

二、建立递归模型

一般情况下通用的递归模型为：
递归函数（）{
   1、递归的出口；
   2、递归调用
   3、递归的本级处
}

第二步和第三步中顺序按照实际情况处理

三、书写递归函数

1. 写出递归定义
2. 套用递归模型根据递归定义写出函数

例如：计算n！

• 递归定义
• 0*!=1（初始值/递归结束界限）
• n!=n* (n-1)!（递归定义）

int fact(int n) {
    if (n <= 1)
        return 1;                       //递归终止条件
    else                
        return fact(n - 1) * n;         //本级递归处理、调用
}

再例如：汉罗塔的递归处理

• 递归定义
• 当柱子上只有一个盘时直接移动（归结束点）
• 当柱子上有多个盘时把倒数第二个盘移动至辅助的柱子上（递归处理）

处理过程如图所示：

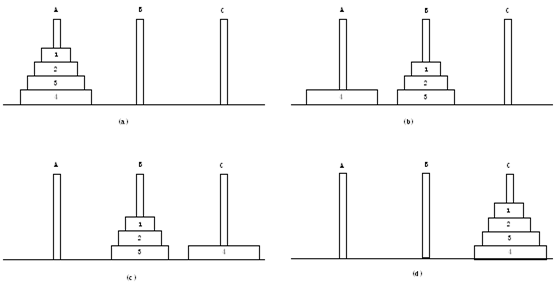
汉罗塔的递归调用（使用空返回值的函数）：
void hanoi(char a ,char b,char c,int n) {
    if (n <= 1) {
        printf("%c -> %c\n",a,c);       //递归终止条件
    }
    else {
        hanoi(a, c, b, n - 1);          //递归调用
        printf("%c -> %c\n", a, c);     //本级递归处理
        hanoi(b, a, c, n - 1);          //递归调用
    }
}