Momentum and NAG

Momentum

Momentum的迭代公式为：
$$\begin{gathered} v_t=\gamma v_{t-1}+\eta {\nabla }_{\theta }J(\theta ) \\ \theta =\theta -v_t \end{gathered}$$
其中$J(\cdot )$一般为损失函数。我们知道，一般的梯度下降，是没有$\gamma v_{t-1}$这一项的，有了这一项之后，$\theta$的更新和前一次更新的路径有关，使得每一次更新的方向不会出现剧烈变化，所以这种方法在函数分布呈梭子状的时候非常有效。

先来看看这个函数利用梯度下降的效果吧。

import matplotlib.pyplot as plt
import numpy as np


"""
z = x^2 + 50 y ^2
2x
100y
"""

partial_x = lambda x: 2 * x
partial_y = lambda y: 100 * y
partial = lambda x: np.array([partial_x(x[0]),
                              partial_y(x[1])])
f = lambda x: x[0] ** 2 + 50 * x[1] ** 2




class Decent:
    def __init__(self, function):
        self.__function = function

    @property
    def function(self):
        return self.__function

    def __call__(self, x, grad, alpha=0.4, beta=0.7):
        t = 1
        fx = self.function(x)
        dist = - grad @ grad
        while True:
            dx = x - t * grad
            fdx = self.function(dx)
            if fdx <= fx + alpha * t * dist:
                break
            else:
                t *= beta
        return dx


grad_decent = Decent(f)

x = np.array([30., 15.])
process = []
while True:
    grad = partial(x)
    if np.sqrt(grad @ grad) < 1e-7:
        break
    else:
        process.append(x)
        x = grad_decent(x, grad)

process = np.array(process)
print(len(process))
x = np.linspace(-40, 40, 1000)
y = np.linspace(-20, 20, 500)
fig, ax= plt.subplots()
X, Y = np.meshgrid(x, y)
ax.contour(X, Y, f([X, Y]), colors='black')
ax.plot(process[:, 0], process[:, 1])
plt.show()

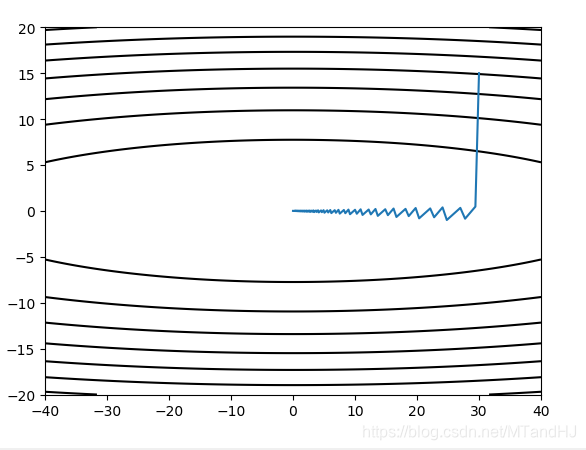
怎么说呢，有点震荡？289步1e-7的误差

x = np.array([30., 15.])
process = []
v = 0
gamma = 0.7
eta = 0.016
while True:
    grad = partial(x)
    v = gamma * v + eta * grad
    if np.sqrt(grad @ grad) < 1e-7:
        break
    else:
        process.append(x)
        x = x - v

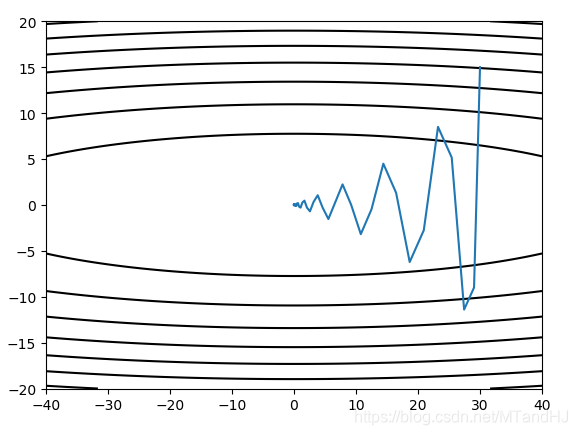
用117步，话说，这个参数是不是难调啊，感觉一般$\eta$很小啊。

还有一个很赞的分析，在博客：
路遥知马力-Momentum

Nesterov accelerated gradient

比Momentum更快：揭开Nesterov Accelerated Gradient的真面目

NGD的迭代公式是：
$$\begin{gathered} v_t=\gamma v_{t-1}+\eta {\nabla }_{\theta }J(\theta -\gamma v_{t-1}) \\ \theta =\theta -v_t \end{gathered}$$
和上面的区别就是，第$t$步更新，我们关心的是下一步(一个近似）的梯度，而不是当前点的梯度，我之前以为这是有一个搜索的过程的，但是实际上没有，所以真的是这个式子具有前瞻性？或许真的和上面博客里说的那样，因为后面的部分可以看成一个二阶导的近似。

x = np.array([30., 15.])
process = []
v = 0
gamma = 0.7
eta = 0.013
while True:
    grad = partial(x-gamma*v)
    v = gamma * v + eta * grad
    if np.sqrt(grad @ grad) < 1e-7:
        break
    else:
        process.append(x)
        x = x - v

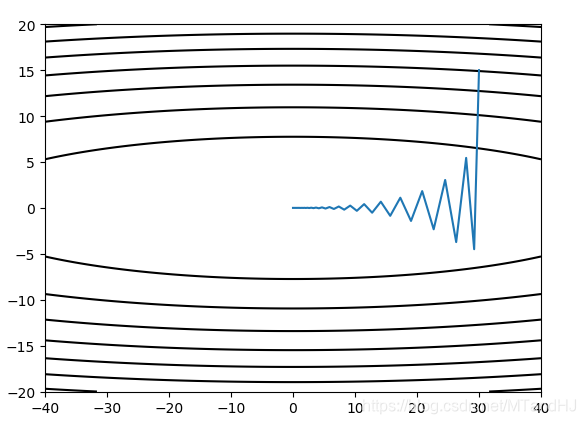
感觉没有momentum好用啊

NESTEROV 的另外一个方法？

在那个overview里面，引用的是

文献链接

但是里面的方面感觉不是NGD啊，不过的确是一种下降方法，所以讲一下吧。

假设$f(x)$满足其一阶导函数一致连续的凸函数，比如用以下条件表示：
$$\Vert f^{\prime }(x)-f^{\prime }(y)\Vert \le L\Vert x-y\Vert ,\forall x,y\in E$$
由此可以推得(不晓得这个0.5哪来的，虽然有点像二阶泰勒展式，但是呢，凸函数好像没有这性质吧，去掉0.5就可以直接证出来了，而且这个0.5对证明没有什么大的影响吧，因为只要让L=0.5L就可以了啊)：
$$f(y)\le f(x)+<f^{\prime }(x),y-x>+0.5L\Vert y-x{\Vert }^2(2)$$

为了解决 min ⁡ { f ( x ) ∣ x ∈ E } \min \{f(x)|x\in E\} min{f(x)∣x∈E}，且最优解$X^{\ast }$非空的情况，我们可以：

0. 首先选择一个点$y_0\in E$,并令
   $$k=0,a_0=1,x_{-1}=y_0,{\alpha }_{-1}=\Vert y_0-z\Vert /\Vert f^{\prime }(y_0)-f^{\prime }(z)\Vert$$
   其中$z$是E中不同于$y_0$的任意点，且$f^{\prime }(y_0)̸=f^{\prime }(z)$
1. 第k 步：
   a) 计算最小的$i$满足：
   $$f(y_k)-f(y_k-2^{-i}{\alpha }_{k-1}{f}^{\prime }(y_k))\ge 2^{-i-1}{\alpha }_{k-1}\Vert f^{\prime }(y_k){\Vert }^2(4)$$
   b) 令
   $$\begin{gathered} {\alpha }_k=2^{-i}{\alpha }_{k-1},x_k=y_k-{\alpha }_k{f}^{\prime }(y_k) \\ {a}_{k+1}=(1+\sqrt{4a_k^2+1})/2 \\ {y}_{k+1}=x_k+(a_k-1)(x_k-x_{k-1})/a_{k+1}. \end{gathered}$$

作者证明了这个方法的收敛率是$O(1/k^2)$的。
即在满足上面提到的假设，且利用上面给出的方法所求，可以证明，对于任意的$k\ge 0$:
$$f(x_k)-f^{\ast }\le C/(k+2{)}^2$$
其中$C=4L\Vert y_0-x^{\ast }{\Vert }^2$并且$f^{\ast }=f(x^{\ast }),x^{\ast }\in X^{\ast }$。
还有一些关于收敛步长的分析就不贴了。

证明：

令$y_k(\alpha )-\alpha f^{\prime }(y_k)$, 可以得到(通过(2))：
$$f(y_k)-f(y_k(\alpha ))\ge 0.5\alpha (2-\alpha L)\Vert f^{\prime }(y_k){\Vert }^2$$
结果就是， 只要$2^{-i}{\alpha }_{k-1}\le L^{-1}$，不等式(4)就成立，也就是说${\alpha }_k\ge 0.5L^{-1}，\forall k\ge 0$, 否则$2^{-i}{\alpha }_{k-1}>L^{-1}$。
令$p_l=(a_k-1)(x_{k-1}-x_k)$，则$y_{k+1}=x_k-p_k/a_{k+1}$,于是：
$$p_{k+1}-x_{k+1}=p_k-x_k+a_{k+1}{\alpha }_{k+1}{f}^{\prime }(y_{k+1})$$
于是：
$$\begin{array}{ll}\Vert p_{k+1}-x_{k+1}+x^{\ast }{\Vert }^2& =\Vert p_k-x_k+x^{\ast }{\Vert }^2+2(a_{k+1}-1){\alpha }_{k+1}<f^{\prime }(y_{k+1},p_k>\\ & +2a_{k+1}{\alpha }_{k+1}<f^{\prime }(y_{k+1},x^{\ast }-y_{k+1}>+a_{k+1}^2{\alpha }_{k+1}^2\Vert f^{\prime }(y_{k+1}){\Vert }^2\end{array}$$
利用不等式(4)和$f(x)$的凸性，可得：
$$\begin{array}{ll}<f^{\prime }(y_{k+1}),y_{k+1}-x^{\ast }>& \ge f(x_{k+1})-f^{\ast }+0.5{\alpha }_{k+1}\Vert f^{\prime }(y_{k+1}){\Vert }^2(5)\\ 0.5{\alpha }_{k+1}\Vert f^{\prime }(y_{k+1}){\Vert }^2& \le f(y_{k+1})-f(x_{k+1})\le f(x_k)-f(x_{k+1})\\ & -a_{k+1}^{-1}<f^{\prime }(y_{k+1},p_k>(6)\end{array}$$
其中第一个不等式，先利用凸函数得性质：
$$f^{\ast }\ge f(y_{k+1})+<f^{\prime }(y_{k+1}),x^{\ast }-y_{k+1})$$
再利用不等式(4):
$$f(y_{k+1})-f(x_{k+1})\ge 0.5{\alpha }_{k+1}\Vert f^{\prime }(y_{k+1}){\Vert }^2$$
代入这俩个不等式可得：
$$\begin{array}{ll}& \Vert p_{k+1}-x_{k+1}+x^{\ast }{\Vert }^2-\Vert p_k-x_k+x^{\ast }{\Vert }^2\le 2(a_{k+1}-1){\alpha }_{k+1}<f^{\prime }(y_{k+1}),p_k>\\ & -2a_{k+1}{\alpha }_{k+1}(f(x_{k+1}-f^{\ast })+(a_{k+1}^2-a_{k+1}){\alpha }_{k+1}^2\Vert f^{\prime }(y_{k+1}){\Vert }^2\\ & \le -2a_{k+1}{\alpha }_{k+1}(f(x_{k+1})-f^{\ast })+2(a_{k+1}^2-a_{k+1}){\alpha }_{k+1}(f(x_k)-f(x_{k+1}))\\ & =2{\alpha }_{k+1}{a}_k^2(f(x_k)-f^{\ast })-2{\alpha }_{k+1}{a}_{k+1}^2(f(x_{k+1}）-f^{\ast })\\ & \le 2{\alpha }_k{a}_k^2(f(x_k)-f^{\ast })-2{\alpha }_{k+1}{a}_{k+1}^2(f(x_{k+1})-f^{\ast })\end{array}$$
其中第一个不等式用到了(5), 第二个不等式用到了(6), 等式用到了$a_{k+1}^2-a_{k+1}=a_k^2$,最后一步用到了${\alpha }_k\le {\alpha }_{k+1}$且$f(x_k)\ge f^{\ast }$。

因此：
$$\begin{array}{ll}& 2{\alpha }_{k+1}{a}_{k+1}^2(f(x_{k+1})-f^{\ast })\le 2{\alpha }_{k+1}{a}_{k+1}^2(f(x_{k+1})-f^{\ast })+\Vert p_{k+1}-x_{k+1}+x^{\ast }{\Vert }^2\\ & \le 2{\alpha }_k{a}_k(f(x_k)-f^{\ast })+\Vert p_k-x_k+x^{\ast }{\Vert }^2\\ & \le 2{\alpha }_0{a}_0^2(f(x_0)-f^{\ast })+\Vert p_0-x_0+x^{\ast }{\Vert }^2\le \Vert y_0-x^{\ast }{\Vert }^2.\end{array}$$
最后一个不等式成立是因为$p_0=0,x_0=y_0$,左边第一项大于等于0.
又${\alpha }_k\ge 0.5L^{-1},a_{k+1}\ge a_k+0.5\ge 1+0.5(k+1)$，所以：
$$f(x_{k+1})-f^{\ast }\le C/(k+3{)}^2$$
证毕。

class Decent:
    def __init__(self, function, grad):
        self.__function = function
        self.__grad = grad
        self.process = []

    @property
    def function(self):
        return self.__function

    @property
    def grad(self):
        return self.__grad

    def __call__(self, y, z):
        def find_i(y, alpha):
            i = 0
            fy = self.function(y)
            fdy = self.grad(y)
            fdynorm = fdy @ fdy
            while True:
                temp = self.function(y - 2 ** (-i) * alpha * fdy)
                if fy - temp > 2 ** (-i -1) * alpha * fdynorm:
                    return i, fdy
                else:
                    i += 1
        a = 1
        x = y
        fdy = self.grad(y)
        fdz = self.grad(z)
        alpha = np.sqrt((y-z) @ (y-z) /
                        (fdy-fdz) @ (fdy - fdz))
        k = 0
        while True:
            k += 1
            self.process.append(x)
            i, fdy = find_i(y, alpha)
            if np.sqrt(fdy @ fdy) < 1:
                print(k)
                return x
            alpha = 2 ** (-i) * alpha
            x_old = np.array(x, dtype=float)
            x = y - alpha * fdy
            a_old = a
            a = (1 + np.sqrt(4 * a ** 2 + 1)) / 2
            y = x + (a_old - 1) * (x - x_old) / a







grad_decent = Decent(f, partial)

x = np.array([30., 15.])
z = np.array([200., 10.])
grad_decent(x, z)
process = np.array(grad_decent.process)
x = np.linspace(-40, 40, 1000)
y = np.linspace(-20, 20, 500)
X, Y = np.meshgrid(x, y)
fig, ax = plt.subplots()
ax.contour(X, Y, f([X, Y]), colors="black")
ax.scatter(process[:, 0], process[:, 1])
ax.plot(process[:, 0], process[:, 1])
plt.show()

用了30步就能到达上面的情况，不过呢，如果想让$\Vert f^{\prime }(x)\Vert \le 1e-7$得1000多步，主要是因为会来回振荡。