Sparse Principal Component Analysis via Regularized Low Rank Matrix Approximation(Adjusted Variance)

前言

这篇文章用的也是交替算法，不得不说，这个东西太好用了，变来变去怎么都能玩出花来。这篇论文的关键之处，我感觉是对adjusted variance的算法，比较让人信服。

文章概述

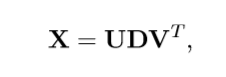
$X是中心化的样本矩阵$

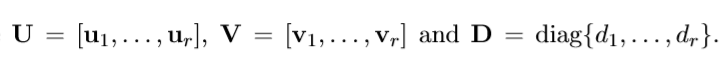
考虑下面的一个最优分解（F-范数）。

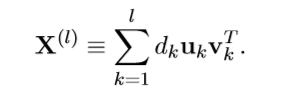
本文采取的也是一种搜索算法，每次计算一个载荷向量，所以，每次都处理的是rank-1的分解。

也就是：

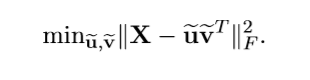
为了稀疏化，必须加上惩罚项，一般的就是1-范数或者0-范数。

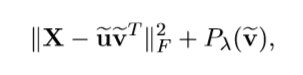
限定$\Vert \tilde{\mathrm{u}}\Vert =1$

固定$\tilde{\mathrm{v}}$

跟之前的论文差不了太多，挺好证的。

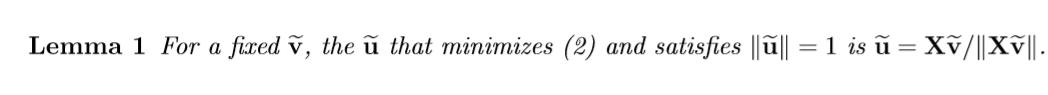
固定$\tilde{\mathrm{u}}$

上述问题，根据下面的改写：

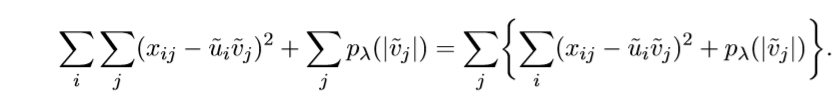
于是就可以分解为多个等价的小问题，每个子问题只需要考虑${\tilde{v}}_j$就可以了。
根据不同的截断手法，有不同的解：

注：对于第一种方法，存疑，因为我证出来的不大一样，当然，可能是我哪里搞错了。
还有一点要注意：因为最后我们要求的其实是载荷向量$\mathrm{v}$，它只需在最后收敛后归一化即可，看下来算法：

Adjusted Variance