【数据结构与算法-排序】常见排序算法的思路解析和代码实现-选择排序

最新推荐文章于 2025-12-19 19:21:47 发布

原创最新推荐文章于 2025-12-19 19:21:47 发布 · 198 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#排序算法 #java #算法

本文介绍了选择排序的基本思想，通过Java代码展示了其实现过程，同时分析了其时间复杂度为O(N^2)和空间复杂度为O(1)。文章还提及选择排序的不稳定性，并对比了与其他排序算法的差异。

选择排序

文章内容
选择排序

文章内容

这是一个系列博客，因为想尽可能的把所有排序的大致思想和代码以及优化方法都做赘述，涉及到篇幅原因可能需要有若干篇博客，每个博客只会写一个排序的算法。本篇是第二种选择排序

分别是
直接插入排序
选择排序
堆排序
冒泡排序
快速排序（重点）
归并排序
还有非基于比较的计数排序
另外还有一个希尔排序，因为时间复杂度问题，这里不做赘述，有想了解的同学可以查找站内其他优质博客。
并且我会解析这七种种排序算法的思想，时间复杂度和空间复杂度，排序算法的稳定性等。
叠甲：本系列博客是我个人为了加深理解以博客形式做的总结，不会特别的深入，如果文章内容有不正确之处欢迎各位大佬指出。

选择排序

思路分析

选择排序的思路非常简单，每次从要排序的数据中找出最小（或最大）的一个元素放在数据的起始位置，一直到没有数据可以进行排序。

下面通过一组图片来进行理解，假设要排序的数组内容是 6 5 7 4 3。
我们定义一个i下标，用来记录要排序内容的起始位置。
定义一个 j 下标， j = i + 1，用来寻找最小值的下标。
定义一个变量minIndex，用来记录最小值的下标。
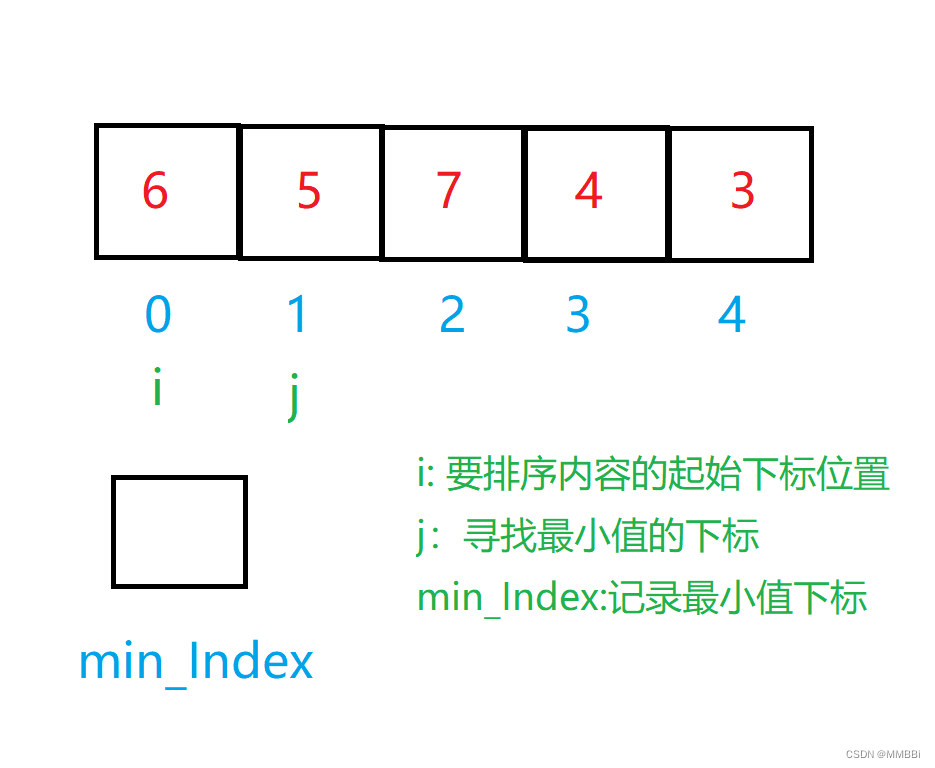
在这里插入图片描述
我们先假设 i 下标的值为最小值，然后用j下标的值去比较 i 下标的值。如果 j下标的值比 i 下标的值小，那么就更新min_Index的值为 j 下标，j 一直走完剩下的数组。最后把i下标的值和 min_Index下标的值交换即可完成一次排序。
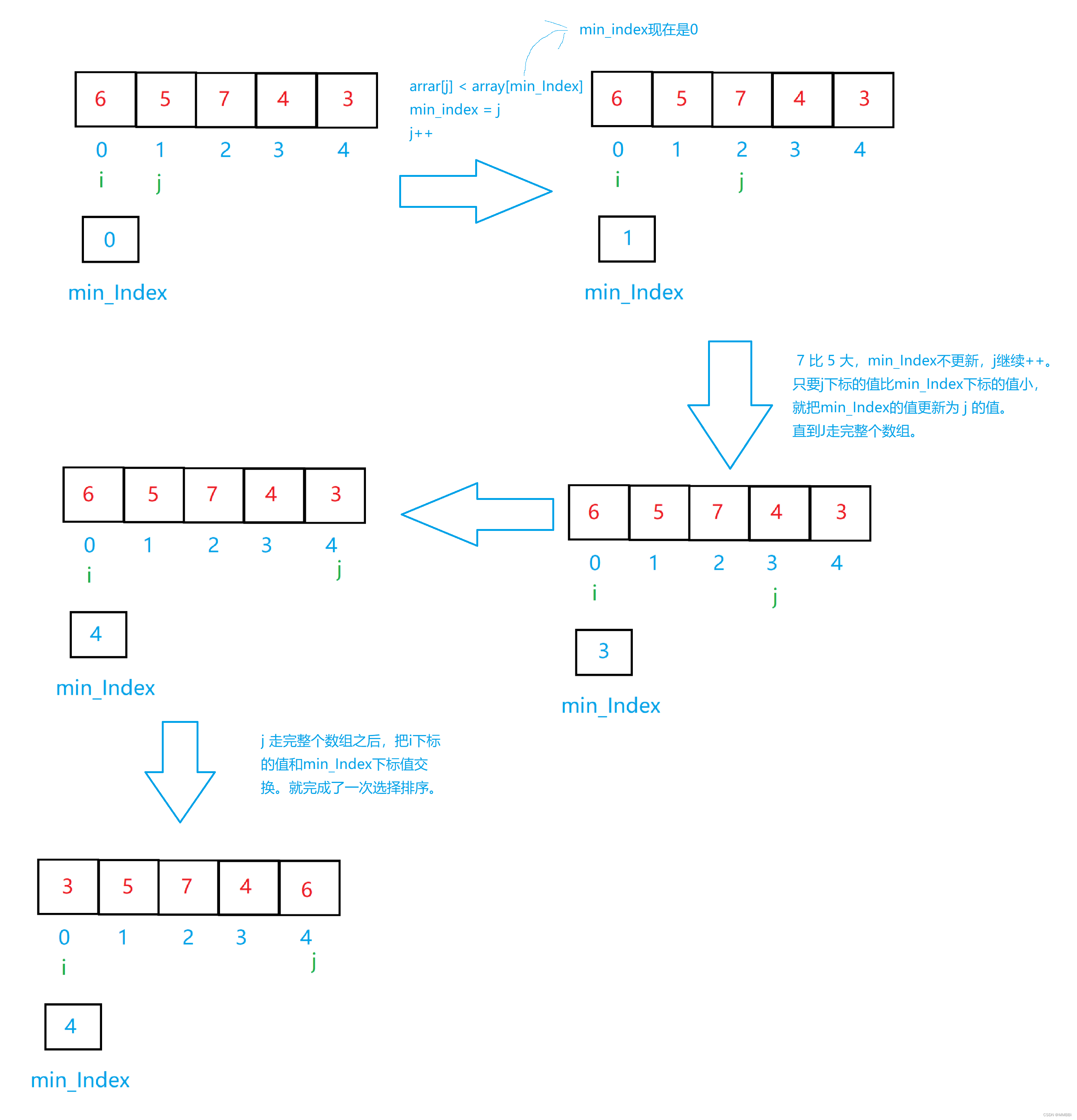
在这里插入图片描述
后面只需要把 i++，继续排剩下的内容即可。

Java代码实现

    public static void selectSort(int[] array) {
        if (array == null) {
            //判断数组是否为空，如果为空则直接return。
            return;
        }
        for (int i = 0; i < array.length; i++) {
            int min_Index = i;//先默认i下标的值就是最小的
            for (int j = i+1; j < array.length; j++) {
                //如果j下标的值比min_Index的值小，更新minIndex
                if (array[j] < array[min_Index]) {
                    min_Index = j;
                }
            }
            //最后交换一下i和minIndex下标的值。
            int tmp = array[i];
            array[i] = array[min_Index];
            array[min_Index] = tmp;
            //这里建议把交换单独写一个方法出来。
            //swap(array, i, min_Index);
        }
    }

   public static void main(String[] args) {
        int[] array = {4, 5, 2, 3, 1, 6, 7, 9, 10, 8};
        Sort.selectSort(array);
        System.out.println(Arrays.toString(array));
    }

在这里插入图片描述
这里再给出第二种写法，定义出minIndex和maxIndex，这样可以一次性找到两个值。不过这个代码不太好理解，并且有坑，仅作补充。这里不做详细解释。时间复杂度上本质上没区别。

   public static void selectSort2(int[] array) {
        int left = 0;
        int right = array.length - 1;
        while (left < right) {
            int min_Index = left;//假设最小值的下标
            int max_Index = left;//假设最大值的下标

            //用for循环找中间的值，更新minIndex和maxIndex下标。
            for (int i = left + 1; i <= right; i++) {
                if (array[i] > array[max_Index]) {
                    max_Index = i;//如果i下标的值比maxIndex下标的值大，更新maxIndex
                }
                if (array[i] < array[min_Index]) {
                    min_Index = i;//如果i下标的值比minIndex下标的值小，更新minIndex
                }
            }
            //交换交换最大和最小值
            swap(array, min_Index, left);//这里可能会出现把最大值给换到最小值的情况
            if (max_Index == left) {
                max_Index = min_Index;
            }
            swap(array, max_Index, right);
            //left和right往中间靠。
            left++;
            right--;
        }