【穆勒矩阵求解线双折射和圆双折射】

最新推荐文章于 2025-12-02 00:16:36 发布

原创最新推荐文章于 2025-12-02 00:16:36 发布 · 855 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#矩阵 #线性代数 #算法

文章详细介绍了如何使用穆勒矩阵从《Accuratemeasurementsofcircularandresiduallinearbirefringenceofspunfibersusingbinarypolarizationrotators》一文中所述的方法，计算并分离光纤中的线双折射和圆双折射。通过测量MD、MR和MΔ，以及应用差分方法处理相位缠绕和波长依赖性，可以提高测量精度并消除不确定性影响。

穆勒矩阵分解
从文章《Accurate measurements of circular and residual linear birefringences of spun fibers using binary polarization rotators》中总结通过穆勒矩阵求解线双折射和圆双折射的计算过程。
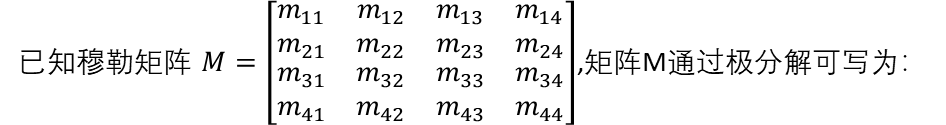
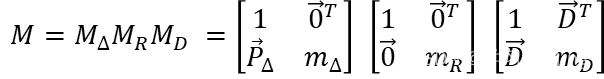
在这里插入图片描述

MD表示测量正交偏振本征态(对应于光纤中常用的偏振相关损耗或PDL)之间的差分损耗的衰减器，MR表示测量两个本征态之间的差分相位的延迟器，MΔ表示表征去偏振的去偏振器。

MD
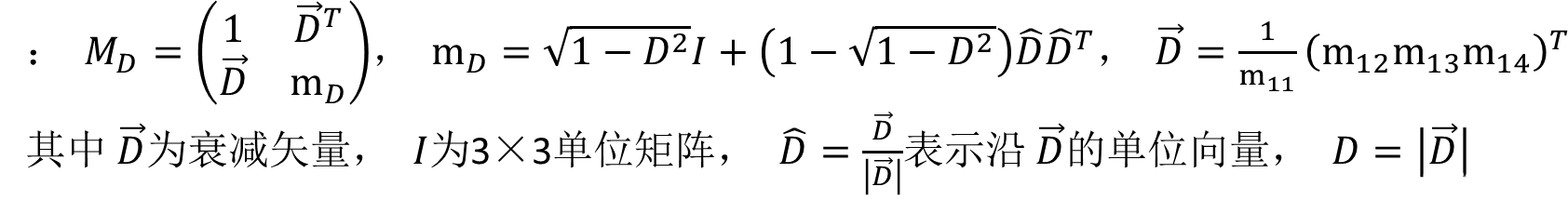
MR

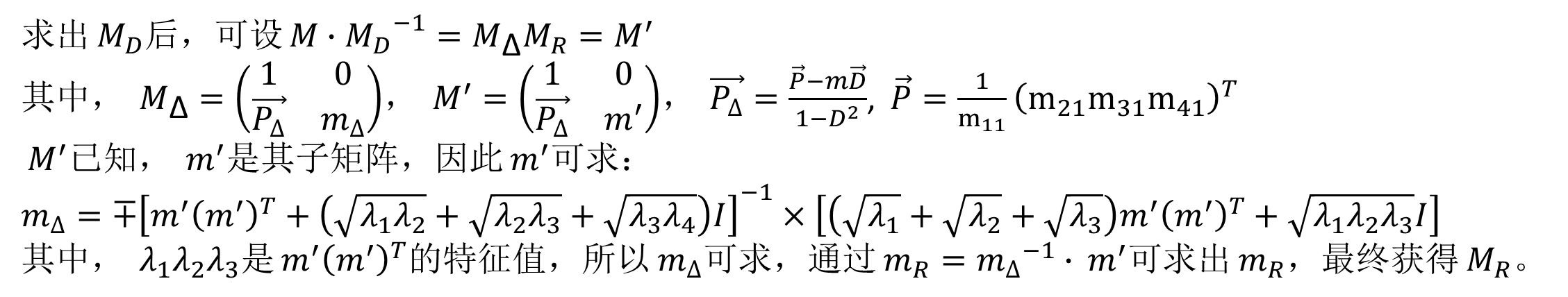
对于被测光纤，总的延迟是∆nL和∆nC（线双折射和圆双折射）的综合效应，因此MR可以分解为两个矩阵：线性延迟为δ且取向角为θ(线性双折射的轴相对于水平轴)的线性延迟矩阵和光学旋转为φ的圆形延迟矩阵：

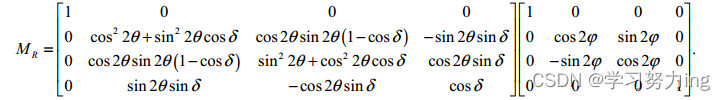
在这里插入图片描述
其中部分元素计算式为

光学旋转φ和线性延迟δ的值可以从矩阵MR中确定

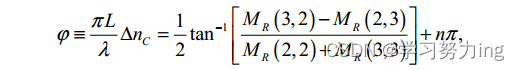
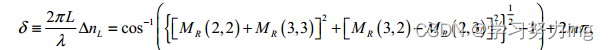
在这里插入图片描述

上式中，m和n是考虑相位缠绕的整数。由于m和n不确定数量，因此在波长λ处很难直接计算出ΔnL和Δnc。在实践中，通过首先在两个相邻波长λ1和λ2处测量φ和δ，即将两个波长代入穆勒矩阵M(λ)中，得到MR(λ1)，MR(λ2)，φ(λ1)，φ(λ2)，δ(λ1)，δ(λ2)，之后计算Δφ=φ(λ1)-φ(λ2)和Δδ=δ(λ1)-δ(λ2)的差值，假设波长步长Δλ=λ2-λ1足够小，使得Δφ和Δδ分别小于π和2π。使用差分方法的优点是1)提高测量精度，2)消除m和n的影响。然后，ΔNc和ΔNl可以使用等式分别从差动旋转角Δφ和差动延迟Δδ获得以下两个式子。
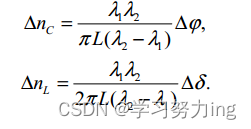
在这里插入图片描述
其中，假设ΔnC和ΔnL在波长上是恒定的，并且这样的假设是准确的，因为如附录B[29]中所讨论的可以忽略双折射色散和小的波长阶跃