数学建模中的线性规划

例1.1 某机床厂生产甲、乙两种机床，每台销售后的利润分别为4千元与3千元。生产甲机床需用A、B机器加工，加工时间分别为每台2小时和1小时;生产乙机床需用A、B、C三种机器加工,加工时间为每台各一小时。若每天

可用于加工的机器时数分别为A机器10小时、B机器8小时和C机器7小时，问该厂应生产甲、乙机床各几台，才能使总利润最大?

上述问题的数学模型:设该厂生产x1台甲机床和x2台乙机床时总利润z最大，则x1 ,x2应满足：

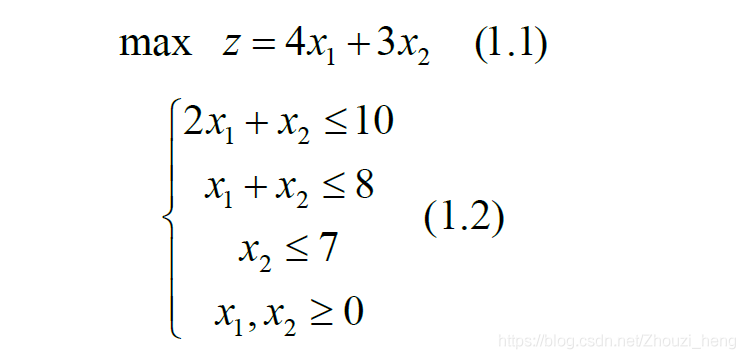
变量x1,x2称之为决策变量，(1.1) 式被称为问题的目标函数，(1.2)中的几个不等式是问题的约束条件,记为s.t.(即subject to)。

目标函数及约束条件均为线性函数，故被称为线性规划问题。

线性规划问题是在-一组线性约束条件的限制下,求一线性目标函数最大或最小的问题。在解决实际问题时，把问题归结成-一个线性规划数学模型是很重要的一步,往往也是很困难的一步，模型建立得是否恰当，直接影响到求解。而选适当的决策变量,是建立有效模型的关键之一。

目标规划和线性规划

目标规划是为了解决多个目标问题而产生的一种数学规划方法，是由线性规划发展演变而来。

目标规划和线性规划主要有以下区别：

线性规划是在一组线性约束条件下，寻求某一单一目标的最优值，只有一个目标函数，但在实际问题中往往要考虑多个目标。

目标规划模型中的目标函数可以有多个目标可以设置，多个目标之间可能是互相矛盾、相互排斥的，每个目标分别带有不同的优先级和权系数；线性规划立足于满足所有约束条件的可行解，而目标规划是在条件下找到满意解,并不一定要满足所有约束，更能运用于实际生活中。