[2022-09-20]神经网络与深度学习第2章-simple classification

classification

写在开头

刚刚结束的数模比赛C题中，关于古文物玻璃提出了一个分类的问题。分类是什么？在词语概念中，分类是按照种类、等级或性质分别归类。同样地，在神经网络与深度学习中也有分类问题，其一般抽象为：对于可以分类的数据样本，通过对其特定参数构建判别模型并进行训练，寻找样本上最优的划分。本次实验我们通过实现简单的两种线性分类模型：Logistic线性回归和Softmax线性回归，对其各部分组成、模型优化以及评价指标进行了解和掌握。

Logistic 回归

Logistic回归是一种非常简单的二分类方式，其通过在线性算子的基础上嵌套一层Sigmoid函数，利用该函数的特性，能够得到较优的分类结果。

• 为什么Sigmoid函数能够二分类？
  答：因为其函数$\sigma (x)=\frac{1}{1+e^{-x}}$，使用代码绘制后图像如下：
  

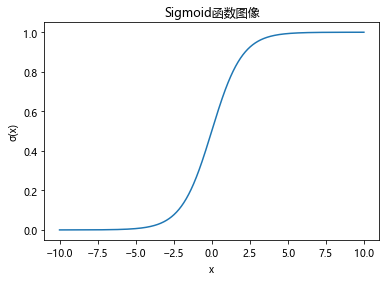
该函数是一个非线性函数，在接近0的区间范围内具有较高的斜率，因此该函数尽可能地将输出分布在接近0或1的部分，所以能够得到较好的二分类效果。

扩展：在二分类中，还有一种常用的二分类函数：tanh，tanh即双曲正切函数，该函数可以看作是Sigmoid的放缩，它将数据尽可能分布在-1和1，在0附近的小区间内函数变化率更大，其公式如下：

$$tanh(x)=\frac{sinhx}{coshx}=(很牛的推导过程)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

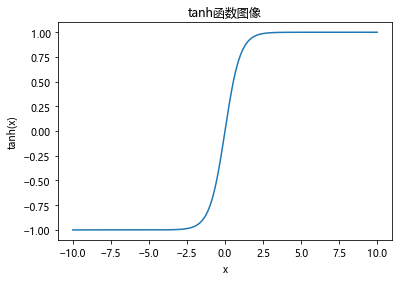
数据集构建

• 数据集构建选取带噪音的两个弯月形状函数，对每个弯月对应一个类别，采集1000条样本，每个样本包含2个特征。

DatasetGenerator类

为了偷懒方便进行数据集构建，我们可以自定义一个生成数据集的类DatasetGenerator。下面是DatasetGenerator的类代码：

class DatasetGenerator():
    def __init__(self):
        self.collections = None
        self.labels_count = 0
        
    def copy(self):
        return self.collections
    
    def copy_from(self, dataset:torch.Tensor):
        self.collections = dataset
    
    def generate(self, inputs, strategy, class_label = None):
        if class_label is None:
            class_label = self.labels_count
        raw = strategy(inputs)
        pairs = torch.hstack([raw,torch.tensor(class_label).repeat(inputs.shape[0],1)])
        if self.collections is None:
            self.collections = pairs
        else:
            self.collections = torch.vstack([self.collections, pairs])
        self.labels_count += 1
        return pairs

    def shuffle(self, seed=None):
        if seed is not None:
            torch.seed(seed)
        if self.collections is None:
            return
        self.collections = self.collections[torch.randperm(self.collections.shape[0])]
        
    def train_test_split(self,
                         use_percentage:bool = True,
                         split_pos:float = 0.8,
                         split_size:tuple = (None, None)):
        if self.collections is None:
            raise Exception('attempted to generate from empty dataset failed')
        n = self.collections.shape[0]
        if use_percentage == True:
            if split_pos <=0 or split_pos >= 1:
                raise Exception('split pos not in range (0, 1)')
        elif split_size[0] + split_size[1] > n:
            raise Exception('split size is greater than max size of dataset : {}'.format(n))
        split_index = int(split_pos * n) if use_percentage else split_size[0]
        dataset_train = self.collections[:split_index]
        if use_percentage == False:
            dataset_test = self.collections[split_index:split_index + split_size[1]]
        else:
            dataset_test = self.collections[split_index:]
        return (dataset_train, dataset_test)

数据生成和可视化

借助数据生成器，生成两个数据类别和生成训练集、验证集、测试集的代码如下：

# 定义数据生成器
dataset = DatasetGenerator()
# 定义两类数据生成函数
def func_claz1(x):
    ox = torch.cos(x).reshape(-1,1) + torch.normal(0,0.05,size=(x.shape[0],1))
    oy = torch.sin(x).reshape(-1,1) + torch.normal(0,0.05,size=(x.shape[0],1))
    return torch.hstack([ox,oy])
def func_claz2(x):
    ox = 1-torch.cos(x).reshape(-1,1) + torch.normal(0,0.05,size=(x.shape[0],1))
    oy = 0.5- torch.sin(x).reshape(-1,1) + torch.normal(0,0.05,size=(x.shape[0],1))
    return torch.hstack([ox,oy])
#生成两类数据
dataset.generate(torch.linspace(0,torch.pi,500),func_claz1,0)
dataset.generate(torch.linspace(0,torch.pi,500),func_claz2,1)
dataset.shuffle()
#生成训练、评估、测试集
dataset_train, dataset_test = dataset.train_test_split(False,split_size=(640,360))
dataset_eval,dataset_test = dataset_test[:160],dataset_test[160:]
# 可视化
plt.rcParams['font.family'] = 'Microsoft YaHei'
plt.scatter(dataset_train[:,0],dataset_train[:,1],label='train',c='r',alpha=0.5)
plt.scatter(dataset_eval[:,0],dataset_eval[:,1],label='eval',c='g',alpha=0.5)
plt.scatter(dataset_test[:,0],dataset_test[:,1],label='test',c='b',alpha=0.5)
plt.title('弯月数据集')
plt.legend()

可得数据集分布如下：

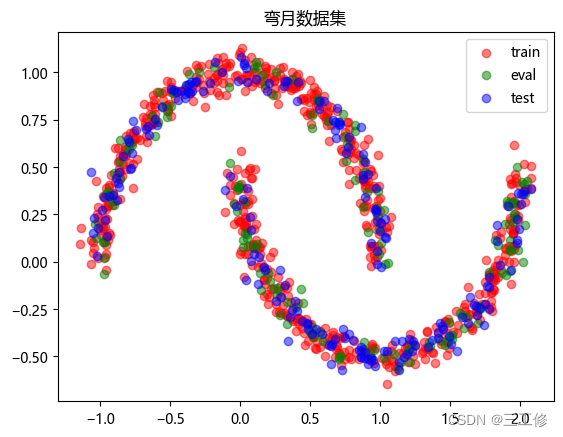
模型构建

前面已经说到，Logistic回归实在线性函数的基础上添加Sigmoid函数即可，其预测标签的后验概率和总体公式如下：
$$\begin{gathered} p(y=1|x)=\sigma (W^{T}x+b), \\ ---分割一下，要不然这两个离太近了--- \\ output=\sigma (W^{T}x+b)=\frac{1}{1+e^{-(W^{T}x+b)}} \end{gathered}$$

• Logistic回归在不同的书籍中，有许多其他的称呼，具体有哪些？你认为哪个称呼最好？
  答：有逻辑回归、逻辑斯蒂回归、还有题目中的Logistic回归。我觉得Logistic回归最好，理由有二：①这是个外文词，翻译太多样了，中文之间叫法不同可能会引起歧义，用原本的英文就算中文不同也没关系；②Logistic长度这么长，属于是水论文字数的利器，具体表现如：这个答案中Logistic这个单词每出现一次要占这么多（doge。
• 什么是激活函数？为什么要用激活函数？常见激活函数有哪些？
  答：激活函数本质上是一种映射关系，将模型的输入进入激活函数，通过激活函数的特点（比如本文中Sigmoid的特点）进行计算并输出得到答案或进入下一层级进行后续计算。

由于该模型实现比较简单，这边直接使用torch进行模型的构建：

class Logistic(torch.nn.Module):
    def __init__(self):
        super(Logistic,self).__init__()
        self.linear = torch.nn.Linear(2,1)
        self.activa = torch.nn.Sigmoid()
        self.linear.weight.data = torch.tensor([[0.,0.]])
        self.linear.bias.data = torch.tensor(0.)
    def forward(self,x):
        return self.activa(self.linear(x))

损失函数

对于分类问题，先然计算数据点偏离程度的均方误差已经不太适合，对此大佬们发明了交叉熵损失函数来解决计算线性分类中计算损失的问题。对于信息熵的概念相信大家都不陌生（不会可以自行百度哈），在二分类问题中，对于每个样本的预测值有一个概率P，显然相对其另一种情况概率为1-P，由此可得损失公式，其中y∈{0,1}为两种类别标签，简单理解可以认为是类别预测错误的信息熵+相对熵：
$$Loss=-(ylogP+(1-y)log(1-P))$$

传送门：这篇解释交叉熵损失写的非常好，比我写的这个四不像好多了

后续实验内容中将介绍多分类的相对熵。

模型优化

有了损失函数和模型的损失值，接下来就是喜闻乐见的模型优化内容了，对于模型优化，我们最简单粗暴的计算方法依旧是梯度下降法^^。
初始模型中，权重和偏置值均为随机，本文定义权重矩阵$W$，偏置值$b$，由此可得：

$$\begin{gathered} \frac{\partial R(W,b)}{\partial W}=-\frac{1}{N}\sum _{n=1}^N{x}^{(n)}(y^{(n)}-{\hat{y}}^{(n)})=-\frac{1}{N}{X}^T(\text{y}-\hat{\text{y}}), \\ ---分割一下，要不然这两个离太近了--- \\ \frac{\partial R(W,b)}{\partial b}=-\frac{1}{N}\sum _{n=1}^N(y^{(n)}-{\hat{y}}^{(n)})=-\frac{1}{N}\sum (\text{y}-\hat{\text{y}}) \end{gathered}$$
偏导数已经得到了，接下来就是更新数据，将原来的$W,b$分别减去学习率$a$乘上前面各自的偏导数即可。这两部分依旧直接使用torch内置，代码如下（关于nndl，代码已经同步至github）：

loss_fn = torch.nn.BCE() # Binary Cross Entropy Loss
logistic = Logistic()
optimizer = torch.optim.SGD(logistic.parameters(),0.01)

评价指标

因为是分类问题，分对才是硬道理，我们这边也只需要用准确率评估分类结果即可：

def accuracy(y,y_pred):
    n = y.shape[0]
    return torch.sum(y == y_pred) / n

完善Runner类

Runner类在之前代码的基础上进行微调，增加特定训练迭代次数输出训练集的指标，代码如下：

class Runner():
    def __init__(self, model, loss_fn, optimizer,eval=None):
        self.model = model
        self.loss_fn = loss_fn
        self.optimizer = optimizer
        if eval is None:
            self.eval = loss_fn
        else:
            self.eval = eval

    def train(self,train_x, train_y,epochs,display_epochs=50):
        for i in range(1,epochs+1):
            pred = self.model(train_x)
            loss = self.loss_fn(train_y,pred)
            self.optimizer.zero_grad()
            loss.backward()
            self.optimizer.step()
            if i % display_epochs == 0:
                print('[{} / {}] loss = {}, acc = {}'.format(i,epochs,loss,accuracy(pred,train_y)))
        
    def eval(self,eval_x,eval_y):
        pred = self.model(eval_x)
        eval_val = self.eval(pred.reshape(-1,1),eval_y)
        return eval_val

    def predict(self,x):
        pred = self.model(x)
        return pred

    def save_model(self, path):
        torch.save(self.model.state_dict(),path)
    
    def load_model(self,path):
        self.model = torch.load(path)

模型训练

通过前面对Runner类的构建，我们能够非常方便地进行模型训练，具体代码如下：

loss_fn = torch.nn.BCELoss()
logistic = Logistic()
optimizer = torch.optim.SGD(logistic.parameters(),0.01)
modelrunner = Runner(logistic,loss_fn,optimizer)
x = dataset_train[:,:-1].squeeze()
y = dataset_train[:,-1].reshape(-1,1)
modelrunner.train(x,y,500,50)

训练输出：

模型评价

使用测试集进行模型评价，计算准确率和损失，这部分代码是前面的简单重复和简单修改，代码如下：

out = logistic_model(dataset_test[:,:-1]).squeeze()
acc = accuracy(out,dataset_test[:,-1])
plt.scatter(dataset_test[:,0],dataset_test[:,1],c=[['red','green'][i] for i in torch.round(torch.squeeze(dataset_test[:,-1])) == torch.squeeze(torch.round(out))])
loss = loss_fn(dataset_test[:,-1],out)
print('acc = {}, loss = {}'.format(acc,loss))

结果如下，其中绿色为分类正确，红色为分类错误：

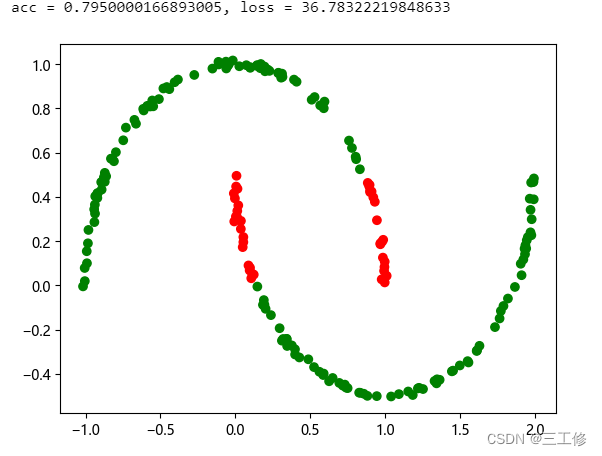
可见模型的效果不错。

基于Softmax回归的多分类任务

我们已经熟悉了简单的二分类问题，进一步扩展便到了多分类问题。我们当然可以使用OvO、OvR和RvR（这三个相信大家在机器学习课上非常熟悉了）将多分类问题转变为二分类问题，但是这样毕竟会构建过多模型导致时间或空间上的大量浪费，于是一个伟大的方法出现了：Softmax回归。

数据集构建

我们采集1000条样本，每个样本包含2个特征。该步骤依旧使用前面制作的DatasetGenerator实现：

# 定义数据生成器
dataset = DatasetGenerator()
# 定义两类数据生成函数
def func_claz1(x):
    ox = 0.2*torch.cos(x).reshape(-1,1) + torch.normal(0,0.1,size=(x.shape[0],1))
    oy = 0.2*torch.sin(x).reshape(-1,1) + torch.normal(0,0.1,size=(x.shape[0],1))
    return torch.hstack([ox,oy])
def func_claz2(x):
    ox = 0.2*torch.cos(x).reshape(-1,1) + torch.normal(0,0.1,size=(x.shape[0],1)) + 1
    oy = 0.2*torch.sin(x).reshape(-1,1) + torch.normal(0,0.1,size=(x.shape[0],1)) + 1
    return torch.hstack([ox,oy])
def func_claz3(x):
    ox = 0.2*torch.cos(x).reshape(-1,1) + torch.normal(0,0.1,size=(x.shape[0],1)) -1
    oy = 0.2*torch.sin(x).reshape(-1,1) + torch.normal(0,0.1,size=(x.shape[0],1)) + 1
    return torch.hstack([ox,oy])
#生成两类数据 使用one-hot编码
dataset.generate(torch.linspace(0,2*torch.pi,1000),func_claz1,[1,0,0])
dataset.generate(torch.linspace(0,2*torch.pi,1000),func_claz2,[0,1,0])
dataset.generate(torch.linspace(0,2*torch.pi,1000),func_claz3,[0,0,1])
dataset.shuffle()
#生成训练、评估、测试集
dataset_train, dataset_test = dataset.train_test_split(False,split_size=(1600,400))
dataset_eval,dataset_test = dataset_test[:200],dataset_test[200:]
# 可视化
plt.rcParams['font.family'] = 'Microsoft YaHei'
plt.scatter(dataset_train[:,0],dataset_train[:,1],label='train',c='r',alpha=0.5)
plt.scatter(dataset_eval[:,0],dataset_eval[:,1],label='eval',c='g',alpha=0.5)
plt.scatter(dataset_test[:,0],dataset_test[:,1],label='test',c='b',alpha=0.5)
plt.title('三个簇数据集')
plt.legend()

数据集分布如下：

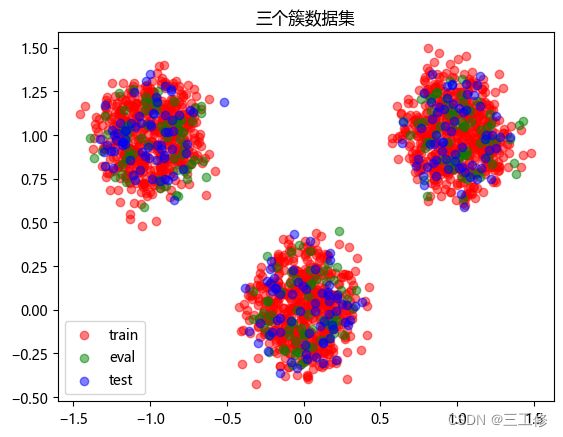
模型构建

要构建Softmax回归的多分类模型，我们首先需要去了解什么是Softmax，其可以将多个标量映射为一个概率分布，公式如下：
$$softmax(x_k)=\frac{e^{x_k}}{{\sum }_{i=1}^K(x_i)}$$
显然可见，Softmax输出构成一个K维的向量，通过和该类真正的标签[0,…,1,…,0]对比才能计算损失，这种标签被称为one-hot编码，通过上述写法也可知类别必须要写成one-hot编码才能进行计算比较。
在预测时如何使用呢？，只需要使用argmax函数得到所分类最高概率的那个标签即可得到最终分类。
模型基于nndl的构建已上传至github，下面给出利用torch直接构建的模型。

• Logistic函数是激活函数。Softmax函数是激活函数么？谈谈你的看法。
  答：当然是。激活函数通过将输入进行特定算子的映射得到对应的特定结果，Softmax也是如此，怎么会不算呢;)

class Softmax(torch.nn.Module):
    def __init__(self):
        super(Softmax,self).__init__()
        self.linear = torch.nn.Linear(2,3)
        self.activation = torch.nn.Softmax()
    def forward(self,x):
        return self.activation(self.linear(x))

损失函数

前面介绍了二分类上的cross entropy loss，扩展到多分类上计算结合one-hot编码后公式非常简单，就是多个类别的二分类交叉熵之和：
$$R(W,b)=-\frac{1}{N}\sum _{n=1}^N(y^{(n)}{)}^{T}log{\hat{y}}^{(n)}$$
由公式也显然可见，交叉熵损失只关心正确类别的预测概率，因此适合分类。

模型优化

模型优化和前面相同，只要构建好对于反向传播的各个梯度项即可，这边我们依旧使用SGD作为优化函数。优化过程详见nndl库和github。

softmax_model = Softmax()
loss_fn = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(softmax_model.parameters(),0.1)

模型训练

模型训练和前面的二分类问题并无二异，这边贴代码也只是水长度而已，因此不再赘述，直接给出训练输出：

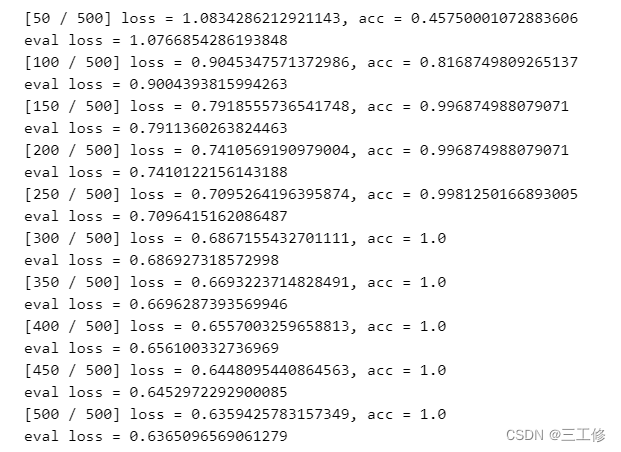
可见训练效果非常好XD。

模型评价

模型评价的代码和前面也几乎完全相同，这边直接给出检验结果，全部分类正确：

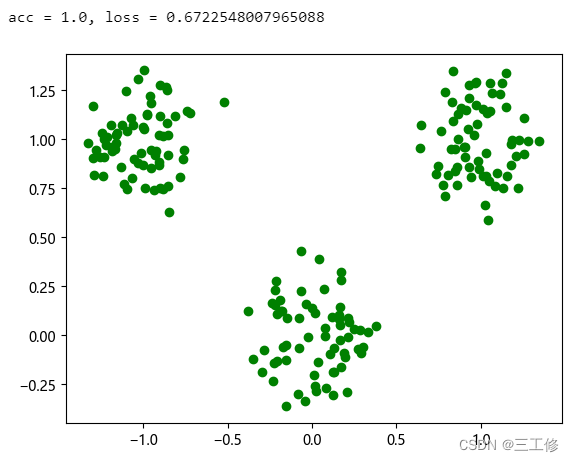
基于Softmax回归完成Iris分类任务

和前面一样，有了模型，我们一定要尝试将其应用在实际数据之上。这里我们使用经典的鸢尾花分类数据集。

数据集的读取、处理和分析

Iris数据集在著名机器学习库sklearn中就有内置，我们将其读出，判断其中有无缺失值或误差值：

from sklearn.datasets import load_iris
dataset = load_iris()

x = torch.tensor(dataset.data)
y_tmp = dataset.target
y = []
for i in y_tmp:
    y.append(list(torch.zeros(3).scatter_(0,torch.tensor(int(i)),value=1).numpy()))
y = torch.tensor(y)

print(torch.isnan(x).any())
print(torch.isnan(y).any())
boxplot(x.numpy())

输出结果如下，可见数据没有缺失值或异常值（想来既然都内置在库里面了，再有这些异常或者缺失也说不过去嘻嘻）。

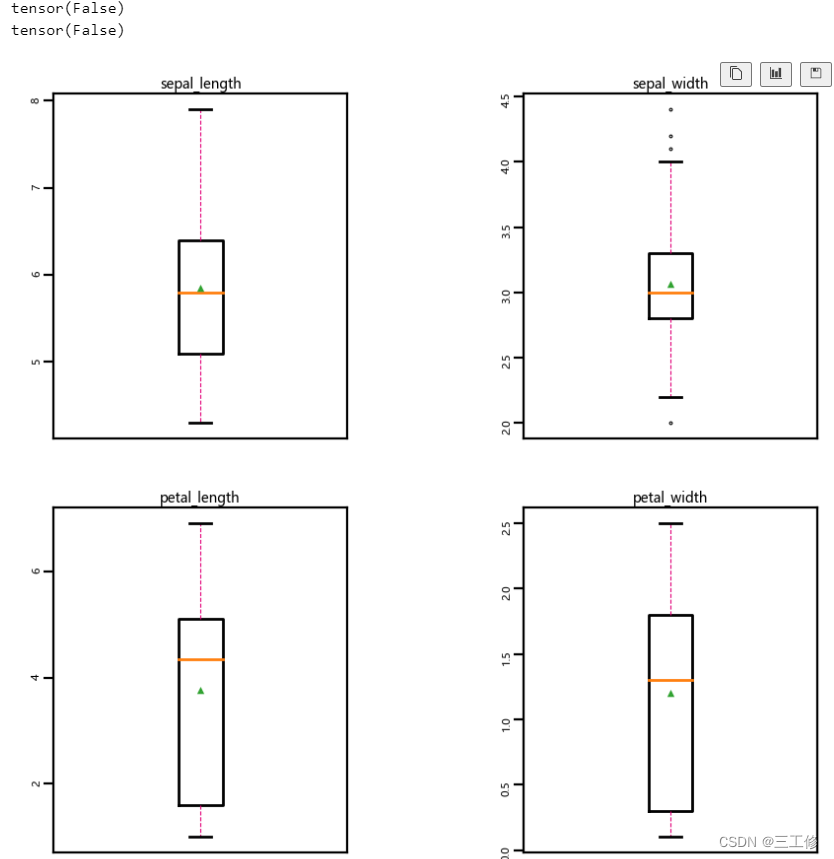
数据划分

这里使用前面定义的DatasetGenerator类进行数据集构建和划分。

dataset_iris = DatasetGenerator()
dataset_iris.copy_from(torch.hstack([x,y]))
dataset_iris.shuffle()
dataset_train,dataset_test = dataset_iris.train_test_split(split_pos=0.8)
n_half = dataset_test.shape[0] // 2
dataset_eval,dataset_test = dataset_test[:n_half],dataset_test[n_half:]

模型构建、损失和优化

前面已经介绍了Softmax函数，这边直接给出代码：

class Softmax(torch.nn.Module):
    def __init__(self):
        super(Softmax,self).__init__()
        self.linear = torch.nn.Linear(4,3)
        self.activation = torch.nn.Softmax()
    def forward(self,x):
        return self.activation(self.linear(x))


model = Softmax()
loss_fn = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(),0.01)
runner = Runner()
runner.train(dataset_train[:,:-3],dataset_train[:,-3:],200,10)

训练的输出结果如下：

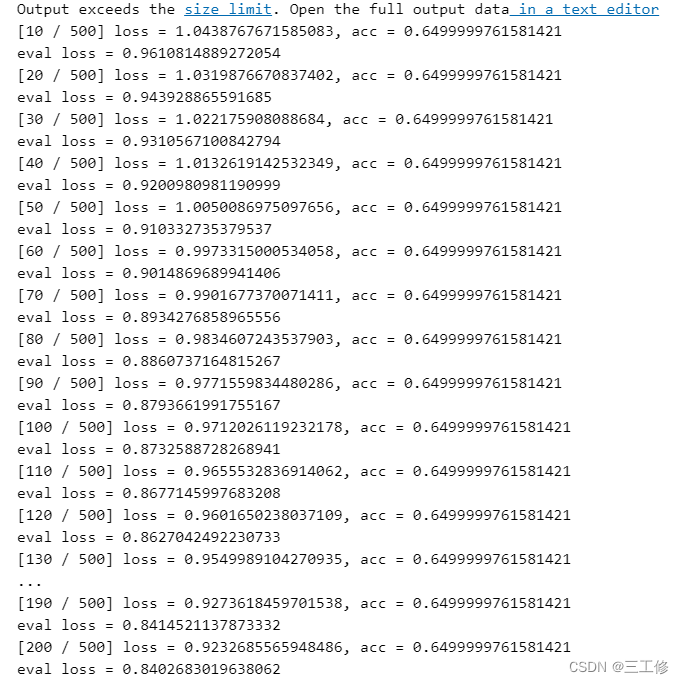
模型评价

模型评价的代码和Softmax也几乎相同，代码如下：

out = model(dataset_test[:,:-3].float())
acc = accuracy(out,dataset_test[:,-3:])
for i in range(out.shape[0]):
    plt.scatter(dataset_test[i,0],dataset_test[i,1],c=['red','green'][torch.argmax(out[i]) == torch.argmax(dataset_test[i,-3:])])
loss = loss_fn(dataset_test[:,-3:],out)
print('acc = {}, loss = {}'.format(acc,loss))

结果如下：

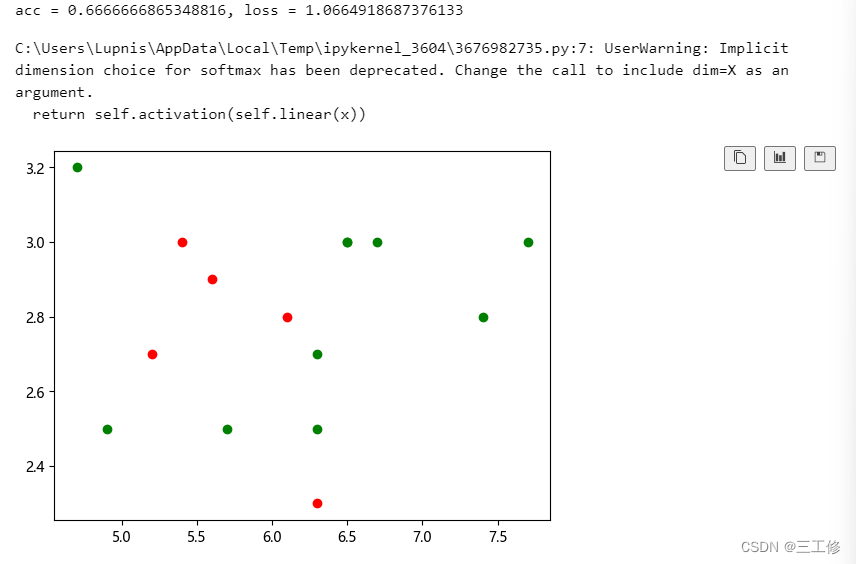
1.调整学习率和训练轮数等超参数，观察是否能够得到更高的精度？

我们使用Iris，将训练代数修改为500，得到：

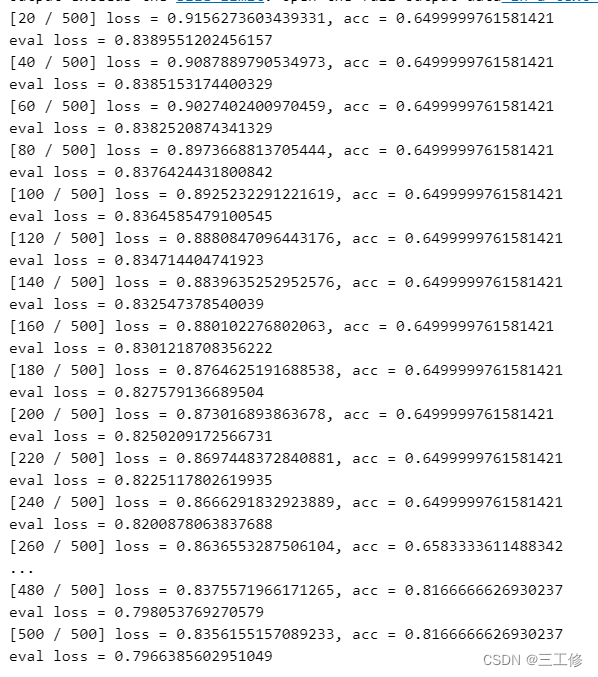
• 结论：适当提升训练轮数，能够提升准确率、降低损失，但是仅限于如Iris这种分割较为简单、不会出现特殊样本的数据集。

将学习率调整至0.1，得到：

• 结论：对于局部极小点不多的数据，适当增大学习率能够使得梯度下降地更快，从而提升精度。

写在最后

这周太忙了，这几天吃了学校的炸鸡还拉肚子，关于拆分成二分类任务的策略，以及使用其他模型进行鸢尾花识别的报告内容，代码已经同步至github，以后可能也许大概会加到实验报告里面，如果没有的话就当留给读者的小练习，可以访问github看看代码xwx。不说了，肚子又痛了救命。