python-leetcode-892. 三维形体的表面积

892. 三维形体的表面积 - 力扣（LeetCode）

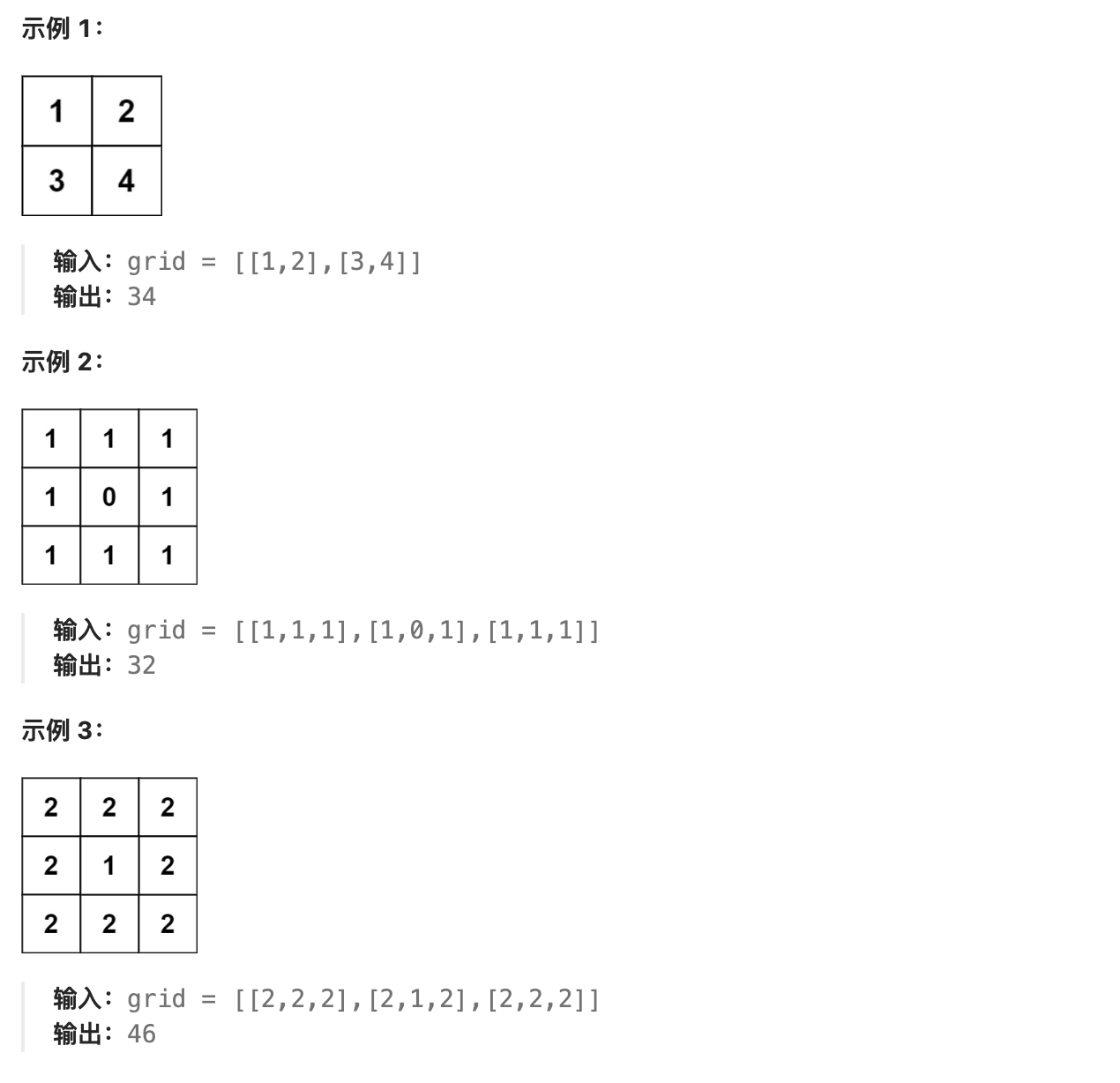
可以按照以下步骤计算总表面积：

1. 初始化总表面积：遍历整个 grid，对于每个 grid[i][j]，如果 v > 0，则贡献 6 * v（每个立方体有 6 个面）。

2. 计算重叠部分：

   • 同一列中，相邻单元格 (i, j) 和 (i+1, j) 之间会粘住 min(grid[i][j], grid[i+1][j]) 个面。

   • 同一行中，相邻单元格 (i, j) 和 (i, j+1) 之间会粘住 min(grid[i][j], grid[i][j+1]) 个面。

3. 最终计算：总表面积 = 初始面积 - 粘连减少的面积。

代码实现：

def surfaceArea(grid):
    n = len(grid)
    area = 0

    for i in range(n):
        for j in range(n):
            if grid[i][j] > 0:
                # 计算该单元格的总表面积
                area += 6 * grid[i][j] - 2 * (grid[i][j] - 1)

            # 减去与上方单元格的粘连部分
            if i > 0:
                area -= 2 * min(grid[i][j], grid[i-1][j])

            # 减去与左侧单元格的粘连部分
            if j > 0:
                area -= 2 * min(grid[i][j], grid[i][j-1])

    return area

复杂度分析：

• 遍历整个 grid，时间复杂度为 O(n^2)。

• 额外只使用了常数级别的空间，空间复杂度为 O(1)。

例子：

输入：

grid = [[1,2],[3,4]]

计算：

• 初始表面积：1*6 + 2*10 + 3*14 + 4*18 = 6 + 10 + 14 + 18 = 48

• 减去粘连部分：

  • 上下相邻 (1,0) 和 (0,0) 贡献 2*min(3,1) = 2

  • 上下相邻 (1,1) 和 (0,1) 贡献 2*min(4,2) = 4

  • 左右相邻 (0,1) 和 (0,0) 贡献 2*min(2,1) = 2

  • 左右相邻 (1,1) 和 (1,0) 贡献 2*min(4,3) = 6

• 总面积 48 - (2 + 4 + 2 + 6) = 34

输出：

print(surfaceArea(grid))  # 34

这个方法高效地计算了最终的表面积，确保所有的粘连部分都正确扣除。