python-leetcode-598. 区间加法 II

598. 区间加法 II - 力扣（LeetCode）

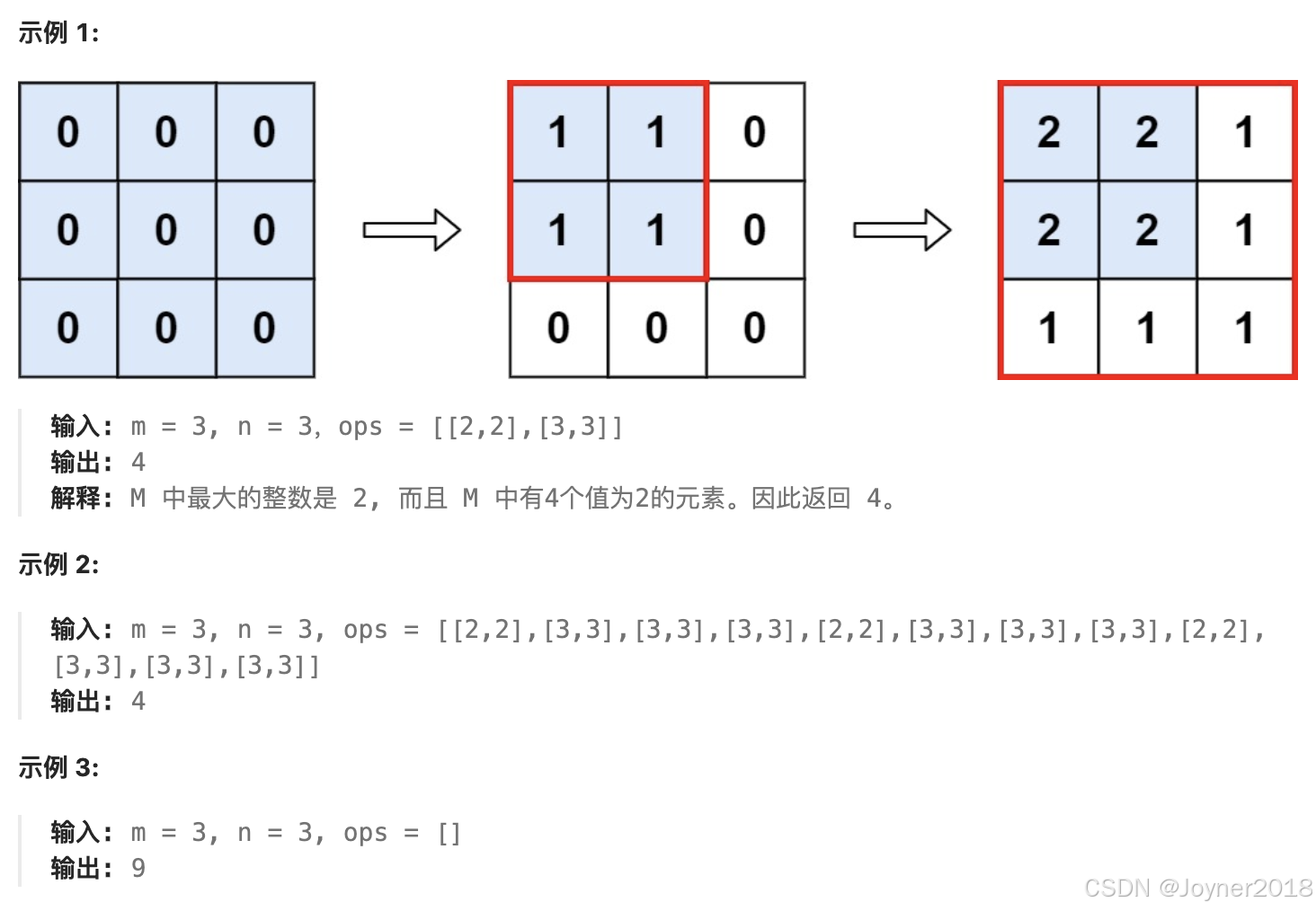
可以通过分析 ops 数组找到影响矩阵值的最小区域。每次操作 [ai, bi] 只会增加 M[0:ai][0:bi] 范围内的值。因此，所有操作的交集决定了矩阵中最大整数的出现次数。

解法：

1. 找到最小的 ai 和 bi：

   • 由于所有的操作都作用在 [0:ai, 0:bi] 这个子矩阵区域，因此最终受影响的最小区域就是所有 ai 中的最小值和所有 bi 中的最小值。
   • 设 min_a = min(ai) 和 min_b = min(bi)，那么最大整数的个数就是 min_a * min_b。

2. 边界情况：

   • 如果 ops 为空，则矩阵中所有元素都是 0，最大整数的个数为整个矩阵的大小 m * n。

代码实现：

def maxCount(m: int, n: int, ops: list[list[int]]) -> int:
    if not ops:
        return m * n  # 没有操作时，整个矩阵都是 0
    
    min_a = min(op[0] for op in ops)
    min_b = min(op[1] for op in ops)
    
    return min_a * min_b

复杂度分析：

• 时间复杂度：O(k)（k 是 ops 的长度，需要遍历 ops 一次）
• 空间复杂度：O(1)（仅使用了常数变量）

示例：

print(maxCount(3, 3, [[2,2],[3,3]]))  # 输出 4
print(maxCount(3, 3, [[2,3],[3,2]]))  # 输出 4
print(maxCount(3, 3, []))            # 输出 9

这样，我们就能快速计算出矩阵中最大整数的个数！ 🚀