Day2.时间复杂度算法

Day2.时间复杂度算法

复杂度分析是整个算法学习的精髓，只要掌握了它，数据结构和算法的内容基本上就掌握了一半。

大 O 复杂度表示法 #趋势

 int cal(int n) {
   int sum = 0; //运行一次
   int i = 1;	//运行一次
   for (; i <= n; ++i) { //运行n次
     sum = sum + i; //运行n次
   }
   return sum; 
 }//总共运行了2n+2次

可以发现： 所有代码的执行时间 T(n) 与每行代码的执行次数 n 成正比。

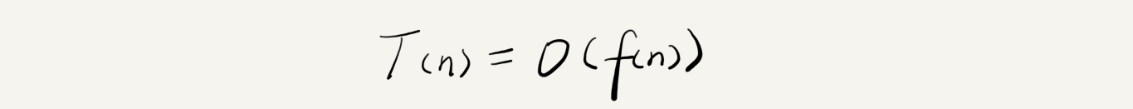
T(n) 表示代码执行的时间；n 表示数据规模的大小；f(n) 表示每行代码执行的次数总和。因为这是一个公式，所以用 f(n) 来表示。公式中的 O，表示代码的执行时间 T(n) 与 f(n) 表达式成正比。

所以例子代码执行时间 T(n) = O(2n+2) 就是大 O 时间复杂度表示法

大 O 时间复杂度实际上并不具体表示代码真正的执行时间，只是表示代码执行时间随数据规模增长的变化趋势，所以，也叫作渐进时间复杂度（asymptotic time complexity），简称时间复杂度。

如何进行时间复杂度分析

1. 只关注循环执行次数最多的一段代码

大 O 这种复杂度表示方法只是表示一种变化趋势 ，通常会忽略掉公式中的常量、低阶、系数，只需要记录一个最大阶的量级就可以啦

我们在分析一个算法、一段代码的时间复杂度的时候，也只关注循环执行次数最多的那一段代码就可以了。这段核心代码执行次数的 n 的量级，就是整段要分析代码的时间复杂度

 int cal(int n) {
   int sum = 0; //运行一次
   int i = 1;	//运行一次
   for (; i <= n; ++i) { //运行n次
     sum = sum + i; //运行n次
   }
   return sum; 
 }

其中第 2、3 行代码都是常量级的执行时间，与 n 的大小无关，所以对于复杂度并没有影响。循环执行次数最多的是第 4、5 行代码，所以这块代码要重点分析。这两行代码被执行了 n 次，所以总的时间复杂度就是 O(n)。 注：不是O(2n)，仔细阅读只关注循环执行次数最多的那一段代码 4,5行代码执行次数一样多，所以只用选取其中一段即可，就是O(n)

2. 加法法则：总复杂度等于量级最大的那段代码的复杂度

int cal(int n) {
   int sum_1 = 0;
   int p = 1;
   for (; p < 100; ++p) { //100
     sum_1 = sum_1 + p;
   }
 
   int sum_2 = 0;
   int q = 1;
   for (; q < n; ++q) { //n
     sum_2 = sum_2 + q;
   }
 
   int sum_3 = 0;
   int i = 1;
   int j = 1;
   for (; i <= n; ++i) { //n
     j = 1; 
     for (; j <= n; ++j) { //n^2
       sum_3 = sum_3 +  i * j; 
     }
   }
 
   return sum_1 + sum_2 + sum_3; //100+n+n^2
 }

代码分为三部分，分别是求 sum_1、sum_2、sum_3。我们可以分别分析每一部分的时间复杂度，然后把它们放到一块儿，再取一个量级最大的作为整段代码的复杂度。

第一段的时间复杂度是多少呢？这段代码循环执行了 100 次，所以是一个常量的执行时间，跟 n 的规模无关。即便这段代码循环 10000 次、100000 次，只要是一个已知的数，跟 n 无关，照样也是常量级的执行时间。当 n 无限大的时候，就可以忽略。尽管对代码的执行时间会有很大影响，但是回到时间复杂度的概念来说，它表示的是一个算法执行效率与数据规模增长的变化趋势，所以不管常量的执行时间多大，我们都可以忽略掉。因为它本身对增长趋势并没有影响。

那第二段代码是O(n)和第三段代码是 O(n^2)

综合这三段代码的时间复杂度，我们取其中最大的量级。所以，整段代码的时间复杂度就为 O(n^2)。也就是说：总的时间复杂度就等于量级最大的那段代码的时间复杂度。那我们将这个规律抽象成公式就是：

如果 T1(n)=O(f(n))，T2(n)=O(g(n))；那么 T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n)))

3. 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

如果 T1(n)=O(f(n))，T2(n)=O(g(n))；那么 T(n)=T1(n)*T2(n)=O(f(n)) * O(g(n))=O(f(n)*g(n)).

常见算法复杂度

对数阶 O(logn)，O(nlogn)

 i=1;
 while (i <= n)  {
   i = i * 2;//这条语句执行了多少次呢？
 }

当i>n时候才停止：i=1 ，2^1，22, 2^3 ,2^x

当 2^x>n时候停止，求出x的值，所以x=log2n ，所以的时间复杂度为O(log2n)

**所有对数阶的时间复杂度都记为 O(logn) **

如果一段代码的时间复杂度是 O(logn)，我们循环执行 n 遍，时间复杂度就是 O(nlogn) 了。而且，O(nlogn) 也是一种非常常见的算法时间复杂度。比如，归并排序、快速排序的时间复杂度都是 O(nlogn)。

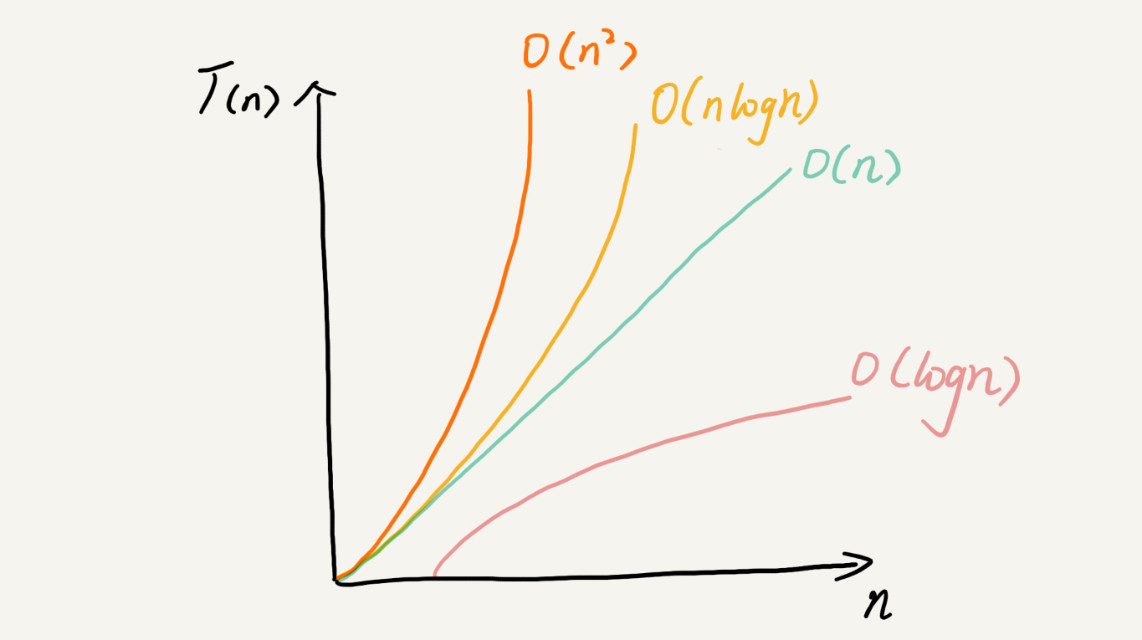
算法复杂度排序