代码随想录算法训练营Day10｜栈与队列Part1

理论知识

概念

队列是先进先出，栈是先进后出

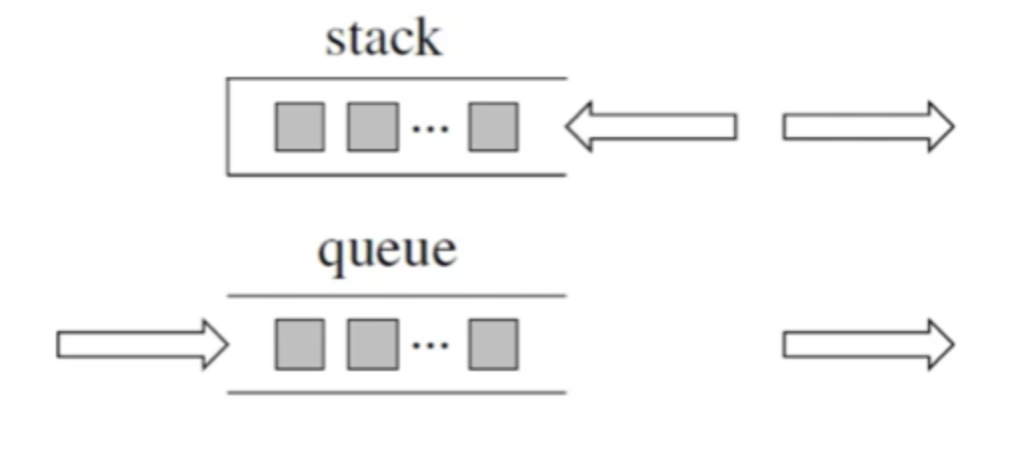
底层实现（Python）

队列：deque实现

python中collections.deque为双端队列，即可以从前端出队，也可以从后端出队。

from collections import deque

q1 = deque()
q1.append(1)
q1.append(2)
q1.append("hello")

q1.popleft()

输出

1

队列：list实现

append 和 deque 的 append 一样，从右侧推入；
pop 可以按照索引抽取，用 index=0 即可抽出最左侧（dqeue的队头）元素。

q2 = []
q2.append(1)
q2.append(2)
q2.append("hello")

q2.pop(0)

输出

1

注意： deque.popleft() 的时间复杂度是O(1)，然而 list.pop(0) 的时间复杂度是O(n) ，列表越长时间复杂度越高。CPython list implementation is array-based. pop(0) removes the first item from the list and it requires to shift left len(lst) - 1 items to fill the gap.

栈：list实现

stack = []
stack.append(1)
stack.append(2)
stack.append("hello")
print(stack)
print("取一个元素：",stack.pop())
print("取一个元素：",stack.pop())
print("取一个元素：",stack.pop())

输出

[1, 2, 'hello']
取一个元素： hello
取一个元素： 2
取一个元素： 1

栈：deque实现

from collections import deque
stack = deque()
stack.append(1)
stack.append(2)
stack.append("hello")

stack.pop()

输出

'hello'

232.用栈实现队列

解题思路

用栈表示队列，需要设置两个栈（stack_in、stack_out），分别用于元素进、出。

代码演示

class MyQueue(object):

    def __init__(self):
        """
	初始化两个空列表作为栈：in主要负责push，out主要负责pop
        """
        self.stack_in = []
        self.stack_out = []
        

    def push(self, x):
        """
        :type x: int
        :rtype: None
        """
        self.stack_in.append(x)


    def pop(self):
        """
        :rtype: int
        """
        if self.empty():
            return None
        
        if self.stack_out:
            return self.stack_out.pop()
        else:
            for i in range(len(self.stack_in)):
                self.stack_out.append(self.stack_in.pop())
            #pop前需要将【入栈】中的元素【全部】塞进【出栈】
            return self.stack_out.pop()
        

    def peek(self):
        """
        :rtype: int
        """
        ans = self.pop()
        self.stack_out.append(ans) #pop后注意放回原栈
        return ans
        

    def empty(self):
        """
        :rtype: bool
        """
        return not (self.stack_in or self.stack_out)

225.用队列实现栈

解题思路

直接利用Python中的双端队列（collections.deque）实现栈的操作

代码演示

from collections import deque

class MyStack(object):

    def __init__(self):
        self.que = deque()

    def push(self, x):
        """
        :type x: int
        :rtype: None
        """
        self.que.append(x)
        

    def pop(self):
        """
        :rtype: int
        """
        if self.empty():
            return null
        else:
            return self.que.pop()    


    def top(self):
        """
        :rtype: int
        """
        if self.empty():
            return None
        else:
            temp = self.que.pop()
            self.que.append(temp)
            return temp
        

    def empty(self):
        """
        :rtype: bool
        """
        return not self.que

20.有效的括号

解题思路

括号匹配是使用栈解决的经典问题。
由于栈结构的特殊性，非常适合做对称匹配类的题目。

写代码前先分析有几种无效字符串的情况：

1. 字符串左方向括号有多余；
2. 左右方向括号无多余，但括号类型不匹配；
3. 字符串右方向括号有多余。
   

代码演示

class Solution(object):
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """
        stack = []
        for char in s:
            if char == "(":
                stack.append(")")
            elif char == "{":
                stack.append("}")
            elif char == "[":
                stack.append("]")
            elif not stack or stack[-1]!= char: #list[-1]表示返回列表最后一个元素
                return False
            else:
                stack.pop()
        
        return True if not stack else False

备注：Python中list切片操作

#list[起始索引:结束索引]切片时包含起始索引位置的元素，但不包含结束索引位置的元素
# 索引为 0表示第一个,1表示第二个,-1表示最后一个,-2表示倒数第二个

# list[-1]：返回最后一个数据
# list[:1]：返回0到1的数据，故返回第一个数据
# list[1:]：返回从1到0的数据,故返回第二个到最后一个的数据（不包含结束索引位置0）
# list[-1:]：返回从-1到0的数据，故返回最后一个数据
# list[:-1]：返回从0到-1的数据，故返回第一个到倒数第二个的数据（不包含结束索引位置-1）
# list[::1]：表示步长为1，步长大于0时，返回序列为原顺序；。
# list[::-1]: 表示从右往左以步长为1进行切片。步长小于0时，返回序列为倒序
# list[::2]: 表示从左往右步长为2进行切片

list = [1, 2, 3, 4, 5]
print(list[-1])  # 5
print(list[:1])  # [1]
print(list[1:])  # [2, 3, 4, 5]
print(list[-1:])  # [5]
print(list[:-1])  # [1, 2, 3, 4]
print(list[::1])  # [1, 2, 3, 4, 5]
print(list[::-1])  # [5, 4, 3, 2, 1]
print(list[::2])  # [1, 3, 5]

1047.删除字符串中的所有相邻重复项

解题思路

将字符串放入栈（append），放入过程中判断是否有相同字母，若有则pop。
需要考虑栈为空的情况，栈为空，直接append。

代码演示

class Solution(object):
    def removeDuplicates(self, s):
        """
        :type s: str
        :rtype: str
        """
        res = list()
        for item in s:
            if res and res[-1] == item: #栈不为空，且有相邻相同字母
                res.pop()
            else:
                res.append(item)
        return "".join(res)  # 字符串拼接（list转str）