目录
写在前面
这是本机器学习小白写的第一篇优快云博客,内容是我学习KNN算法时的一些笔记,后面的案例练习是我对课程实验作业的一次详细复盘。一些关键代码中不太明白的部分,是询问了AI大模型得到并总结的解答(感谢豆包豆老师手把手教学
希望能用自己的一点输出对抗AI时代的存在焦虑
一、KNN算法介绍
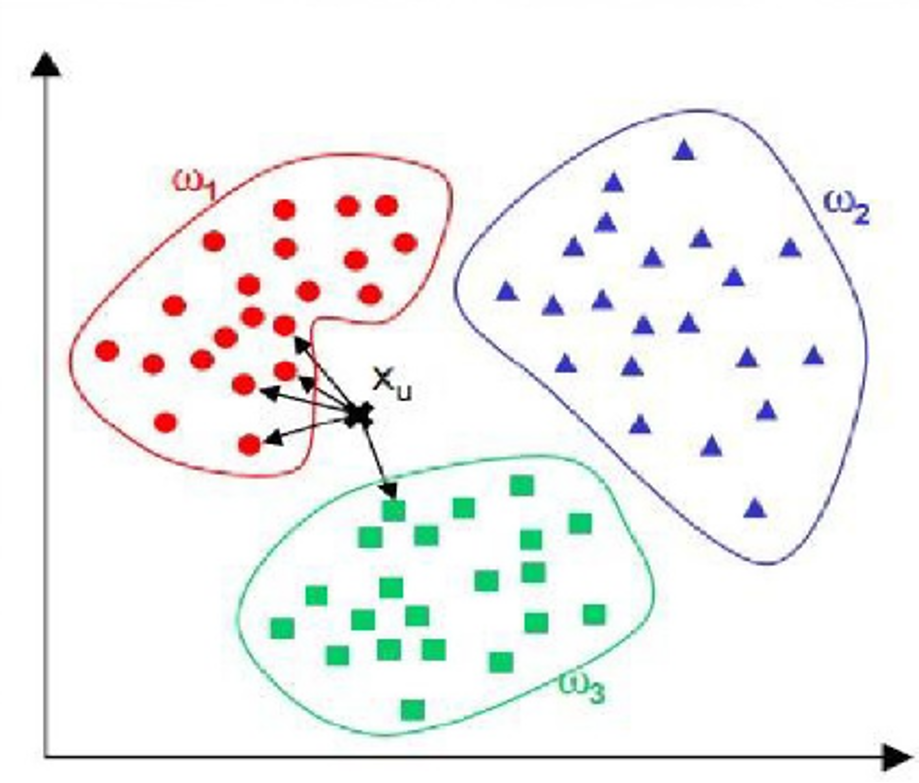
KNN,即K-nearest neighbor,翻译过来为k个最近的邻居,是一种最直接的用来分类未知数据的方法。其核心逻辑为:未知样本的类别由其周围 k 个最近邻样本的类别通过多数投票决定。算法无需预先训练模型参数,仅在预测时计算未知样本与所有训练样本的距离,选择距离最近的 k 个样本作为邻居,最终将邻居中出现频率最高的类别作为未知样本的预测类别。
简单来说,KNN可以看成:有一堆已经分好类的数据,然后当一个新数据进入的时候,就开始跟已知数据里的每个点求距离,然后挑出离新数据最近的K个点,看看这K个点属于什么类型,然后用少数服从多数的原则,给新数据归类。
二、算法改进
1.从降低计算复杂度的角度
当样本容量较大以及特征属性较多时,KNN算法分类的效率就会大大降低。
改进方法有:
- 对样本属性进行约简,删除那些对分类结果影响较小(说明不太重要)的属性
- 缩小训练样本:在原有样本中删除一部分与分类不太相关的样本,或只选取一部分的代表样本
- 通过聚类,将聚类所产生的中心点作为新的训练样本。
2.从优化相似度度量方法的角度
基本的KNN算法基于欧式距离来计算样本的相似度,这种方法对噪声特征非常敏感。
为了改变传统KNN算法中特征作用相同的缺陷,可在度量相似度的距离公式中给特征赋予不同权重,特征的权重一般根据各个特征在分类中的作用设定。
也可采用不同的度量方法,如余弦距离。
3.从选取k值的角度
k值选择过小,得到的neighbor过少,会降低分类精度,同时也会放大噪声数据的干扰;而k值选择过大,如果待分类样本属于训练集中数据量较少的那一类,那么在选择k个近邻的时候,实际上并不相似的数据也被包含进来,造成噪声增加而导致分类效果的降低。
通常采用误差平衡法和交叉验证法。
- 误差平衡法:选定训练集和测试集,将k由小变大逐渐递增,计算测试误差,制作k与测试误差的曲线图。
- 交叉验证法:对于较小的数据集,为了分离出测试集合而减小训练集合是不明智的,因为最佳的k值显然依赖于训练数据集中数据点的个数,一种有效的策略就是采用“留出一个”交叉验证,即留一验证,代替之前的一次性验证来选择k值。留一交叉验证是交叉验证的极限形式,适用于小样本场景:
- 将 N 个样本依次作为验证集(每次 1 个样本),剩余 N-1 个样本作为训练集;
- 对每个待测试的 k 值,循环 N 次训练与验证,计算 N 次预测的平均准确率;
- 选择平均准确率最高的 k 值作为最优参数。
三、案例练习:
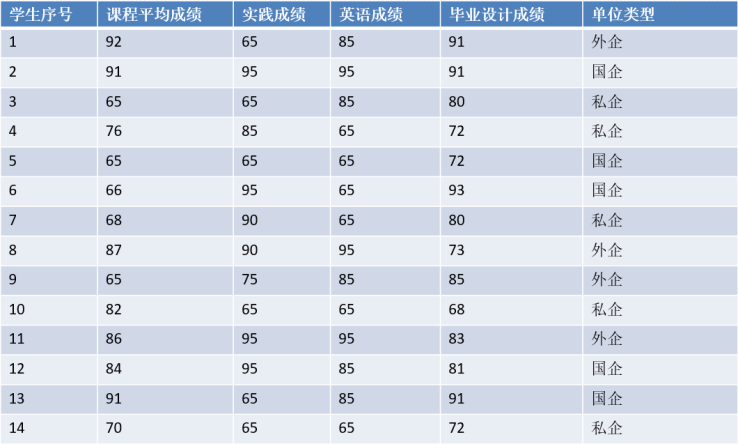
数据样例如下,其中各个属性权重分别为(1,0.7,0.9,0.5)
实验环境:
编程语言:Python 3.8+
核心库:pandas(数据处理)、numpy(数值计算)、scikit-learn(模型构建与评估)
开发环境:Jupyter Notebook
引入库:
import pandas as pd
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split,GridSearchCV,LeaveOneOut
from sklearn.metrics import accuracy_score, classification_report
1.数据加载与预处理
使用pandas库创建一个包含 14 条学生成绩记录的 DataFrame
# -------------------------1.创建数据集-------------------------
data={
'学生序号': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14],
'课程平均成绩': [92, 91, 65, 76, 65, 66, 68, 87, 65, 82, 86, 84, 91, 70],
'实践成绩': [65, 95, 65, 85, 65, 95, 90, 90, 75, 65, 95, 95, 65, 65],
'英语成绩': [85, 95, 85, 65, 65, 65, 65, 95, 85, 65, 95, 85, 85, 65],
'毕业设计成绩': [91, 91, 80, 72, 72, 93, 80, 73, 85, 68, 83, 81, 91, 72],
'单位类型': ['外企', '国企', '私企', '私企', '国企', '国企', '私企', '外企',
'外企', '私企', '外企', '国企', '国企', '私企']
}
df = pd.DataFrame(data)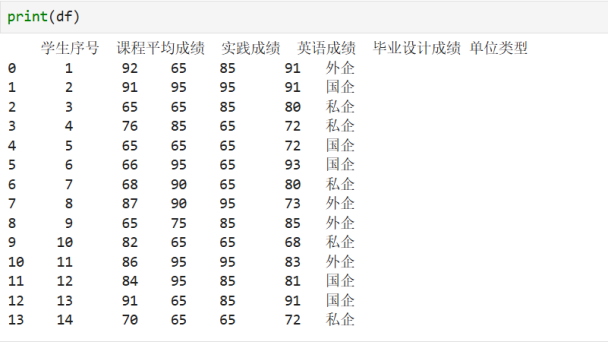
分离特征与标签,为分类标签编码
# ------------------------2.数据预处理------------------------------
# 2.1 分离特征(X)和标签(y)
X=df[['课程平均成绩', '实践成绩', '英语成绩', '毕业设计成绩']].values
# 标签:单位类型(转换为数字编号)
label_map={'私企':0,'国企':1,'外企':2}
y=df['单位类型'].map(label_map).values
# 2.2应用属性权重(对标准化后的特征加权)
weights=np.array([1,0.7,0.9,0.5])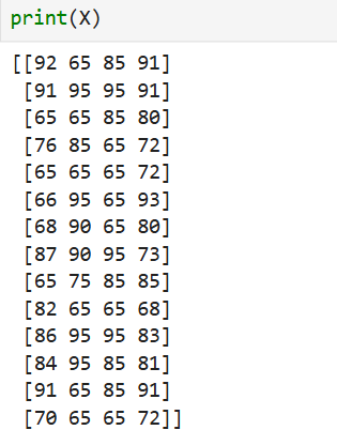

2.自定义相似度度量计算函数:
相似度度量方法如下
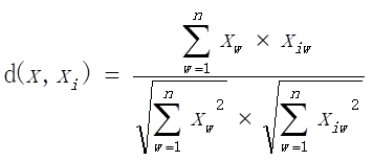
如未知样本为x=(75, 80, 85, 85),各属性权重分别为(1, 0.7, 0.9, 0.5),采用新的度量方式计算方式为
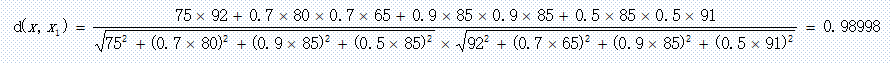
传统余弦相似度用于衡量两个向量的方向一致性,而加权余弦距离在其基础上引入特征权重,突出重要特征对相似度计算的影响,公式如下:
加权向量计算:x_weighted=x×w(x为原始特征向量,w为特征权重向量)
点积计算:numerator=dot(x1_weighted,x2_weighted)
意义:衡量两个向量 “方向是否一致”。点积越大,说明两个学生在 “加权特征” 上的整体趋势越像(比如都在重要特征上得分高)。
范数乘积计算:denominator=norm(x1weighted)×norm(x2weighted)
意义:对 “点积” 做「标准化」。因为点积会受向量 “长度” 影响(比如一个学生所有特征得分都很高,点积自然大),分母可以抵消这种影响,让最终结果落在 [-1, 1] 之间(余弦相似度的范围),方便横向对比。
加权余弦相似度:similarity=denominator*numerator
结果越接近 1:两个样本越相似(比如这个例子中,学生 1 和 2 的加权相似度很高)
结果越接近 - 1:两个样本越不相似
结果 = 0:两个样本完全无关
距离转换:distance=1−similarity(满足 sklearn 中 “距离越小越相似” 的要求)
# -----------------------3.加权余弦距离函数---------------------------
def weighted_cosine_distance(x1,x2):
x1_weighted=x1*weights
x2_weighted=x2*weights
# 分子:加权后向量的点积
numerator=np.dot(x1_weighted,x2_weighted)
# 分母:加权后向量的L2范数的乘积
denominator=np.linalg.norm(x1_weighted)*np.linalg.norm(x2_weighted)
#返回相似度(余弦距离 = 1 - 余弦相似度,这里直接返回相似度用于KNN的“距离越小越相似”逻辑)
return 1-(numerator/denominator)3.留一交叉验证优化k值
要注意的是,KNN 中偶数 k 易出现 “投票平局”(如 2 个邻居分属不同类别),模型会随机选择类别,导致预测稳定性下降。通常 KNN 会选择奇数 k避免该问题。
# ---------------------- 4. 交叉验证确定最优k值 ----------------------
# 4.1 定义待搜索的k值范围
param_grid = {'n_neighbors': [3,5,7,9,11,13]}
# 4.2 初始化KNN分类器(距离函数固定为自定义的加权余弦距离)
knn = KNeighborsClassifier(metric=weighted_cosine_distance, algorithm='brute',n_neighbors=7)这段代码是初始化一个自定义距离的KNN分类器,核心是告诉 KNeighborsClassifier:“用我自己定义的加权余弦距离来计算样本相似度,并且用暴力搜索的方式找邻居”。KNeighborsClassifier 是 sklearn内置的K近邻分类器类 —— 它封装了 KNN 算法的核心逻辑(找邻居、投票分类),我们只需要通过参数配置,就能直接使用(不用自己写 “找 top-K 个邻居”“多数投票” 的代码)。
代码详解:
metric=weighted_cosine_distance
-
metric的作用:定义 KNN 算法中 “如何计算两个样本之间的距离 / 相似度”。KNN 的核心是 “找和测试样本最像的 K 个邻居”,而 “像不像” 就由metric决定。 -
默认的
metric:sklearn 默认用「欧氏距离(Euclidean Distance)」,比如两个学生的特征向量直接算直线距离。这里自定义:weighted_cosine_distance,即不使用默认方法,用我们自己写的加权余弦距离函数判断样本到底像不像。
algorithm='brute'(算法选择)
-
algorithm的作用:定义 KNN 如何 “高效找到测试样本的 K 个邻居”(即 “近邻搜索算法”)。 -
brute的含义:brute翻译为中文是 “暴力”,它的逻辑最简单直接:当要预测一个测试样本时,把测试样本和训练集中的每一个样本都计算一次距离,然后对所有距离排序,取距离最小的前 K 个作为邻居。
-
为什么要用
brute:因为用了 自定义距离函数——sklearn 中的其他高效搜索算法(比如kd_tree或ball_tree)只支持 sklearn 内置的距离(如欧氏距离、曼哈顿距离),不支持用户自定义的距离函数。所以必须用algorithm='brute',强制 KNN 用 “暴力搜索” 的方式,才能适配自定义距离。(如果样本量很大,暴力搜索会变慢)
n_neighbors=5
- 默认找 5 个邻居,这就是我们之前用交叉验证要优化的 “k 值”,后面会通过
GridSearchCV替换成最优 k
# 初始化LOOCV(每个样本单独当验证集)
loo = LeaveOneOut() # 等价于cv=N(N=14)
# 4.3 初始化GridSearchCV
# 用GridSearchCV执行LOOCV
grid_search_loo = GridSearchCV(
estimator=knn,
param_grid=param_grid,
cv=loo, # 关键:用LOOCV替代5折
scoring='accuracy', # 用准确率(1-平均误差)作为评价指标
n_jobs=-1,
verbose=1
)
# 执行LOOCV
grid_search_loo.fit(X, y)LeaveOneOut():负责 “怎么划分训练集和验证集”—— 每个样本轮流当唯一的验证集,其余 N-1 个当训练集,不用传任何参数,它会自动识别你数据的样本数 N(14 个样本,就自动分成 14 组 “训练集 + 验证集”)。
GridSearchCV:负责 “自动干活”—— 按 LOOCV的规则,对每个待测试的 k 值,跑一遍完整的 LOOCV 验证,算准确率,最后挑最优 k。参数解释如下:
1. estimator=knn
- 传入之前定义的 KNN 分类器:
knn - 意思是:“我要优化的模型就是这个 KNN”—— 后续所有 k 值的验证,都基于这个 KNN 的基础配置
2. param_grid=param_grid
param_grid是之前定义的 “待测试 k 值列表”({'n_neighbors': [1,3,5,7,9]})- 意思是:“请你帮我把这些 k 值一个个试一遍,每个 k 都用 LOOCV 验证,最后看哪个 k 最好”
3. cv=loo
- 传入前面初始化的 LOOCV 工具,指定 “用 LOOCV 方式做交叉验证”
4. scoring='accuracy'
- 定义 “怎么判断 k 值好不好”—— 用 “准确率”(正确预测的样本数 / 总样本数)作为评价标准。
- 因为 LOOCV 是 N 次验证,所以每个 k 值会得到 N 个 “单样本预测结果”,
scoring='accuracy'会自动计算这 N 次的平均准确率( 正确次数 / N)。 - 补充:如果是回归问题,会用
scoring='mse'(均方误差),但这里是分类问题,用准确率最合适。
5. n_jobs=-1
- 优化计算速度:让电脑用所有 CPU 核心同时计算不同 k 值的 LOOCV,不用逐个 k 排队算(对小样本影响不大,但养成习惯很好)
- 如果改成
n_jobs=1,就是只用 1 个核心,计算会慢一点
6. verbose=1
- 控制输出日志:
0表示 “不输出中间过程”,1表示 “输出每个 k 的计算进度”(比如 “正在计算 k=3 的 LOOCV”)
grid_search_loo.fit(X, y)是 “触发执行” 的代码:运行后,GridSearchCV会按照上面的配置,自动完成所有工作。
输出如下:
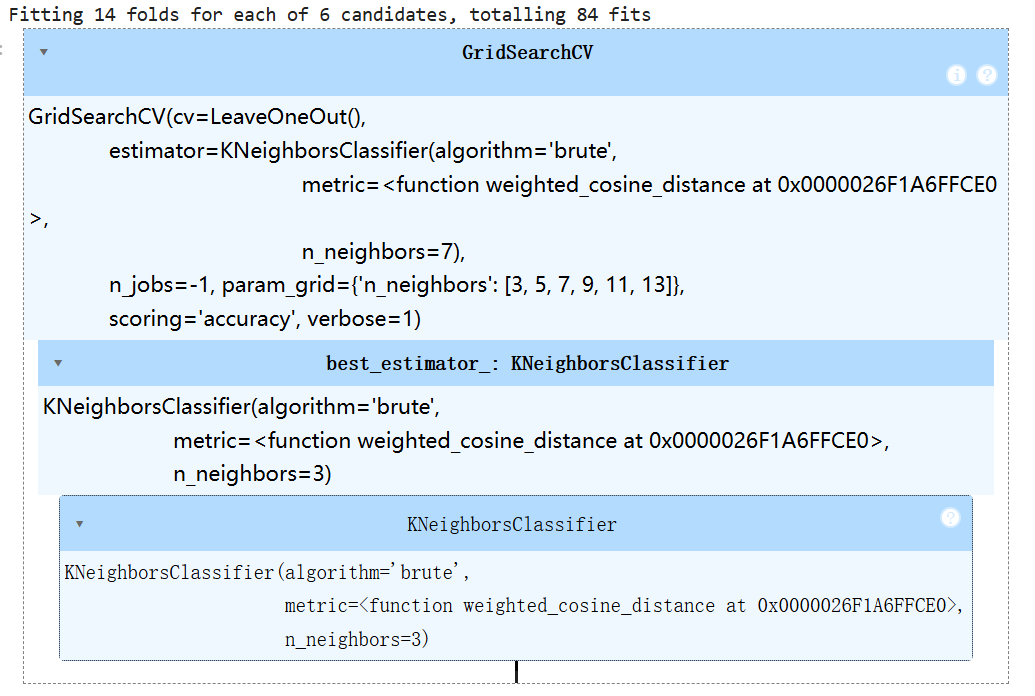
交叉验证结果输出:
# 4. 输出LOOCV结果(重点看平均准确率)
print("="*60)
print("LOOCV交叉验证结果(每个样本单独当验证集):")
print("="*60)
print(f"最优k值:{grid_search_loo.best_params_['n_neighbors']}")
print(f"最优k对应的LOOCV平均准确率:{grid_search_loo.best_score_:.4f}")
print(f"最优k对应的LOOCV平均误差:{1 - grid_search_loo.best_score_:.4f}") # 平均误差=1-平均准确率
print("\n所有k值的LOOCV表现:")
for k, acc in zip(grid_search_loo.cv_results_['param_n_neighbors'], grid_search_loo.cv_results_['mean_test_score']):
print(f"k={k} → 平均准确率:{acc:.4f} | 平均误差:{1-acc:.4f}")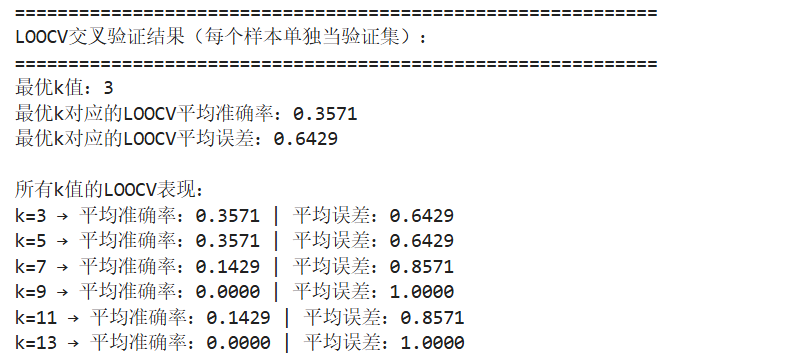
4.构建最终KNN模型
通过grid_search_loo.best_params获取最优 k 值(比如{'n_neighbors': 3})
按照7:3划分训练集与测试集,用最优k值训练模型
# 5.3 用最优k训练最终模型
best_k = grid_search_loo.best_params_['n_neighbors']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)
final_knn = KNeighborsClassifier(n_neighbors=best_k, metric=weighted_cosine_distance, algorithm='brute')
final_knn.fit(X_train, y_train)
5.模型评估
计算测试集准确率,生成分类报告
# 5.4 模型评估(测试集上的表现)
y_pred = final_knn.predict(X_test)
test_accuracy = accuracy_score(y_test, y_pred)
print("\n" + "="*60)
print(f"最终模型(最优k={best_k})测试集评估:")
print("="*60)
print(f"测试集准确率:{test_accuracy:.4f}")
print("\n分类报告:")
print(classification_report(y_test, y_pred, target_names=label_map.keys()))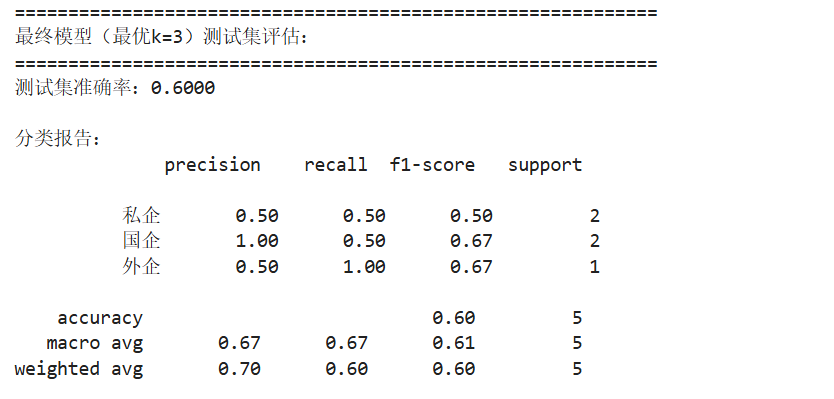
按类别拆解指标(精确率、召回率、F1-score):
私企:精确率 = 0.50、召回率 = 0.50:2 个真实私企样本中,模型正确识别 1 个;预测为 “私企” 的样本中,仅 50% 是真实私企。综合 F1-score=0.50,表现中等。
国企:精确率 = 1.00、召回率 = 0.50:模型预测为 “国企” 的样本全部是真实国企(精确率满分),但仅识别出 2 个真实国企中的 1 个。F1-score=0.67,综合表现较好。
外企:精确率 = 0.50、召回率 = 1.00:1 个真实外企样本被模型正确识别(召回率满分),但模型预测为 “外企” 的样本中,只有 50% 是真实外企。F1-score=0.67,对仅 1 个样本的类别来说表现合理。
6.新样本预测
def predict_company(new_data):
"""
预测新学生的单位类型
new_data: 列表,格式[课程平均成绩, 实践成绩, 英语成绩, 毕业设计成绩]
"""
new_data = np.array(new_data).reshape(1, -1) # 转为模型需要的格式
pred_label = final_knn.predict(new_data)[0] # 预测标签(数字)
return {v: k for k, v in label_map.items()}[pred_label] # 转回单位类型名称
# 测试预测
new_student = [88, 90, 92, 85] # 示例数据
pred_result = predict_company(new_student)
print(f"\n新学生数据:{new_student}")
print(f"预测单位类型:{pred_result}")

7.数据可视化
需提前引入相关第三方库
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import confusion_matrix
# 设置中文字体(解决Jupyter中文显示问题)
plt.rcParams['font.sans-serif'] = ['SimHei'] # Windows用黑体,Mac用['Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题(1)交叉验证结果准确率对比图
# ---------------------- 不同k值的交叉验证准确率对比图 ----------------------
# 提取交叉验证结果(k值和对应的平均准确率)
k_list = [3, 5, 7,9,11,13]
cv_acc_list = [grid_search_loo.cv_results_['mean_test_score'][i] for i in range(len(k_list))]
best_k_idx = k_list.index(best_k) # 最优k的索引
# 创建图表
plt.figure(figsize=(10, 6))
bars = plt.bar(k_list, cv_acc_list, color='lightblue', edgecolor='black', alpha=0.7)
# 给最优k值的柱子标红,突出显示
bars[best_k_idx].set_color('red')
bars[best_k_idx].set_alpha(0.8)
# 添加数值标签
for bar, acc in zip(bars, cv_acc_list):
height = bar.get_height()
plt.text(bar.get_x() + bar.get_width()/2., height + 0.01,
f'{acc:.4f}', ha='center', va='bottom', fontsize=10)
# 设置标题和标签
plt.title('不同k值的留一交叉验证平均准确率', fontsize=14, fontweight='bold')
plt.xlabel('k值(邻居数量)', fontsize=12)
plt.ylabel('平均准确率', fontsize=12)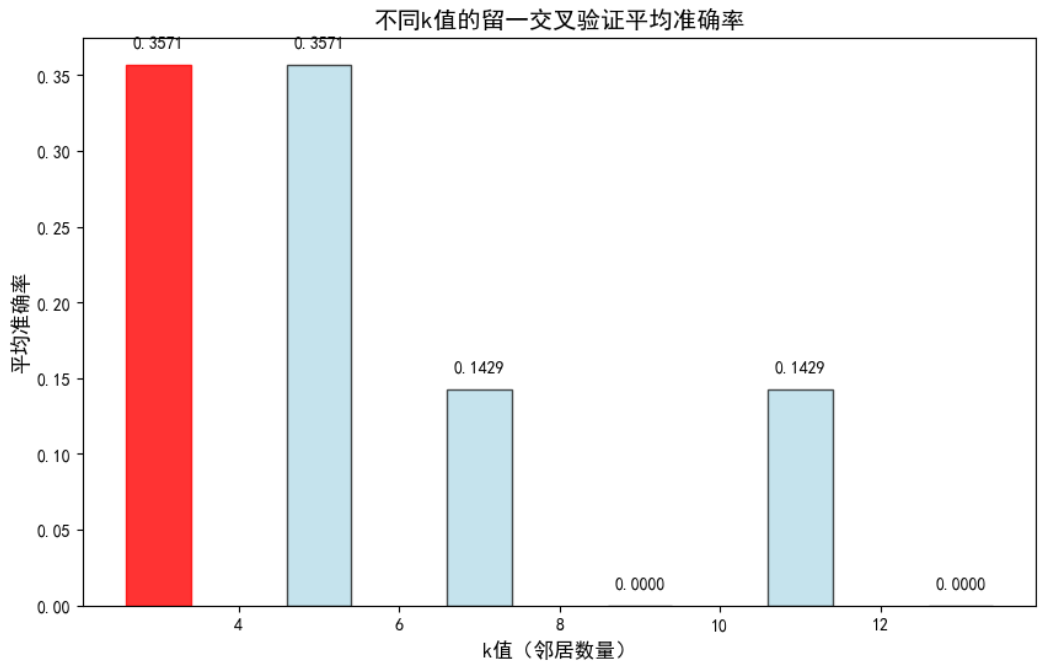
(2)混淆矩阵热力图
# ---------------------- 2. 测试集分类混淆矩阵 ----------------------
# 计算混淆矩阵(真实标签vs预测标签)
cm = confusion_matrix(y_test, y_pred)
class_names = ['私企', '国企', '外企'] # 类别名称
# 创建混淆矩阵热力图
plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues',
xticklabels=class_names,
yticklabels=class_names)
# 设置标题和标签
plt.title(f'KNN模型(k={best_k})测试集混淆矩阵', fontsize=14, fontweight='bold')
plt.xlabel('预测标签', fontsize=12)
plt.ylabel('真实标签', fontsize=12)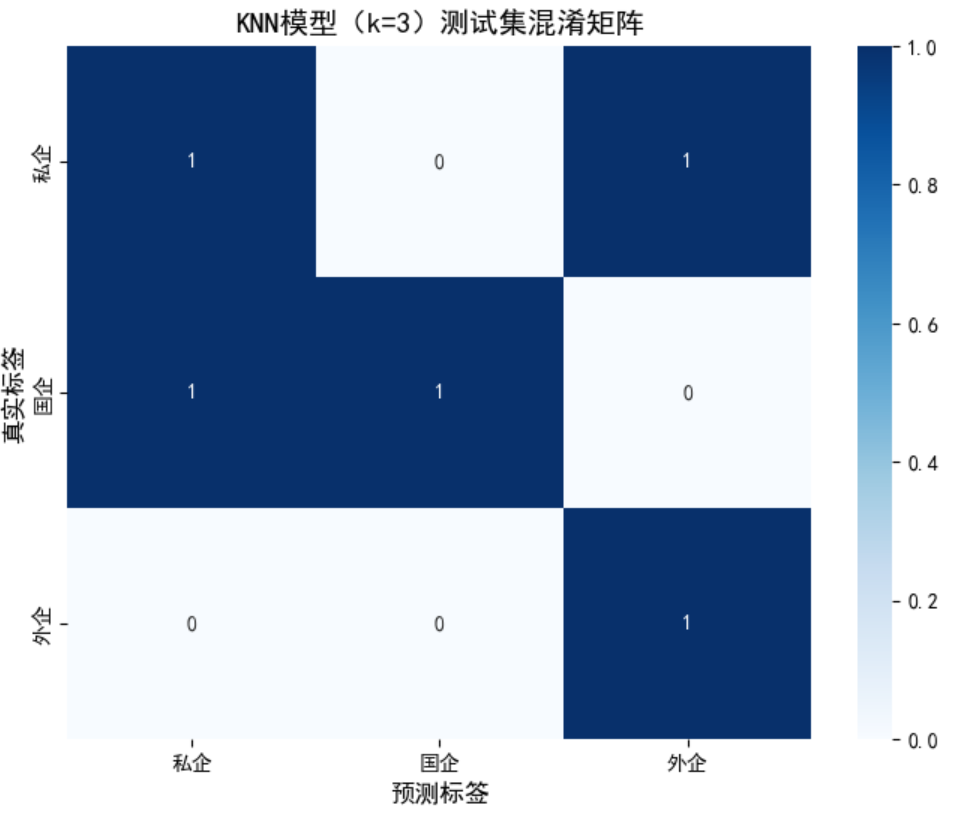
(3)样本特征分布散点图
# ---------------------- 3. 样本特征分布散点图(课程成绩vs英语成绩) ----------------------
# 选择2个重要特征(课程平均成绩+英语成绩)做散点图,颜色区分类别
plt.figure(figsize=(8, 6))
colors = ['red', 'green', 'blue'] # 私企=红,国企=绿,外企=蓝
markers = ['o', 's', '^'] # 不同类别用不同标记
# 遍历每个类别绘图
for label, class_name in enumerate(class_names):
mask = y == label # 该类别的样本掩码
plt.scatter(X[mask, 0], X[mask, 2], # X[mask,0]=课程成绩,X[mask,2]=英语成绩
c=colors[label], marker=markers[label], s=80, alpha=0.7,
label=class_name, edgecolors='black')
# 标注测试集样本(用黑色边框放大显示)
for i, (x, y_label) in enumerate(zip(X_test, y_test)):
plt.scatter(x[0], x[2], c=colors[y_label], marker=markers[y_label],
s=200, edgecolors='black', linewidth=2, alpha=0.9)
# 标注预测结果(正确=黑色,错误=红色)
pred_label = y_pred[i]
text_color = 'black' if y_label == pred_label else 'red'
plt.annotate(f'测试{i+1}\n{class_names[pred_label]}',
xy=(x[0], x[2]), xytext=(5, 5), textcoords='offset points',
fontsize=9, color=text_color, fontweight='bold')
# 设置标题和标签
plt.title('样本特征分布(课程平均成绩 vs 英语成绩)', fontsize=14, fontweight='bold')
plt.xlabel('课程平均成绩', fontsize=12)
plt.ylabel('英语成绩', fontsize=12)
plt.legend(loc='best')
plt.grid(alpha=0.3)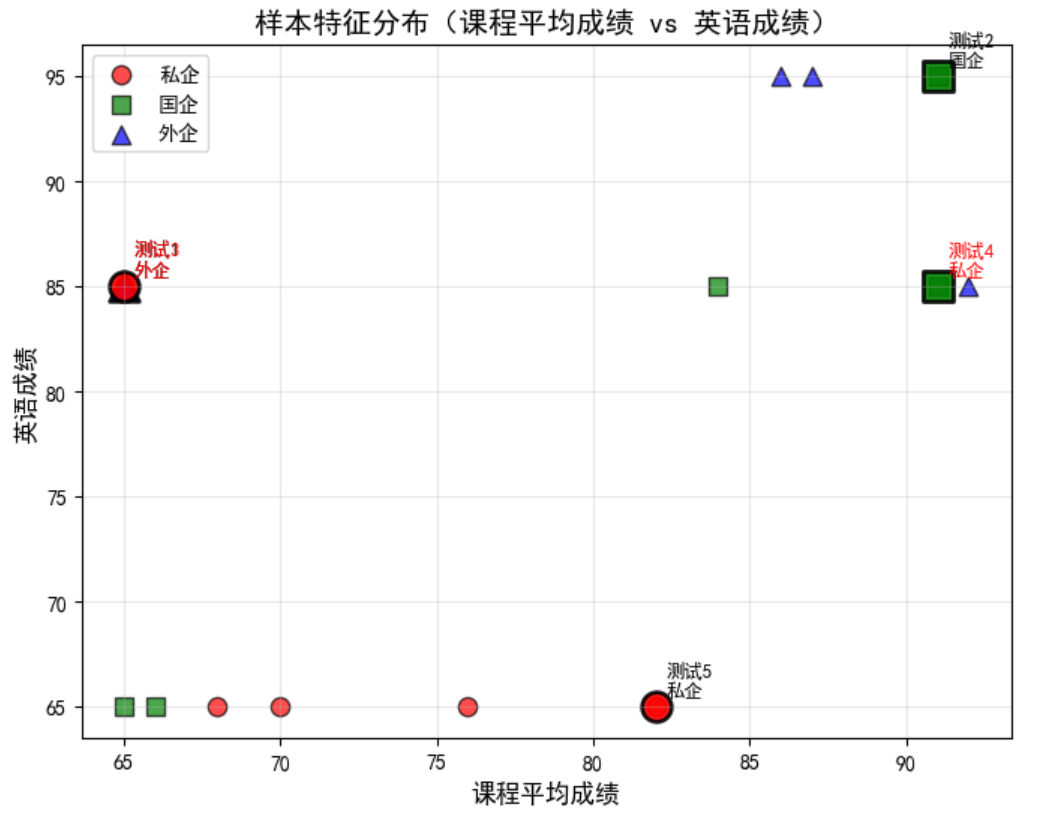
用 “课程平均成绩” 和 “英语成绩”(两个高权重特征)展示所有样本的分布,颜色 / 标记区分类别,黑色边框标注测试集样本;
能看到不同类别样本的特征聚集情况(比如外企样本是否在高英语成绩区域),以及测试集样本的预测对错(红色标注为预测错误,黑色为正确)
 KNN算法详解与实战优化
KNN算法详解与实战优化




















 2434
2434

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








