【机器学习实战3】、基于统计的分类方法：朴素贝叶斯

朴素贝叶斯

假设你被诊断出患有非常罕见的疾病，这种病患的比例仅是人口的0.1％，即每千人中有1人。
你参加的检查这种疾病的检测能正确地找出99%的患者，将健康的人错误分类的几率只有1%。
那么你有多少概率真正患病呢，回答：99%。完了,贝叶斯老爷子的棺材板压不住了。
答案为9%。
P（患病 | 检测为阳性）= P（患病）P（检测为阳性 | 患病）/P（检测为阳性）=0.001 * 0.99/ (0.999 *0.01+ 0.001 *0.99) =0.09
那如果再测第二次依然为阳性，真正患病的概率为多少呢。
此时只需将上面的0.01即患病率改为0.09，0.999改为0.91，
结果为0.91

一、贝叶斯最优分类器及公式推导

分类任务就是将样本正确分类，在分类时将预测结果与样本真实分类的差距，定义为损失，

对分类任务来说，在所有相关概率都已知的理想情形下，贝叶斯决策论考虑如何基于这些概率和误判损失来选择使损失最小的类别标记。

有M个样本要分类，即X{x1，x2,…,Xm}，假设有N个可能的类别标记，即Y ={c1,c2,…,cN}

λij 表示将一个真实标记为ci的样本x误分类为cj所产生的损失。

那么将一个真实标记为ci的样本x分类为每一个可能类别的概率乘以λij，再累加
即为将x分类为ci所产生的损失，称为“条件风险” R(ci | x)

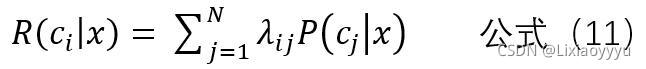
条件风险只是一个样本的风险，总体风险就是将所有样本分类的损失。

目的是寻找一个 h：X ->Y（h表示X到Y的映射），以最小化总体风险。

只要h能最小化每一个样本的条件风险，那么总体风险也将被最小化

这就产生了贝叶斯判定准则：为最小化总体风险，只需在每个样本上选择那个能使条件风险 R(c | x)最小的类别标记

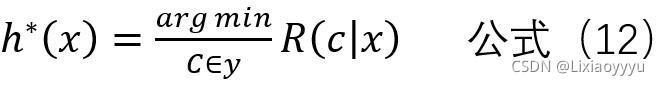
此时，h *称为贝叶斯最优分类器。

如目标是最小化条件风险。那么误判损失λij
if i=j，λij =0，ortherwise λij=1.

此时条件风险

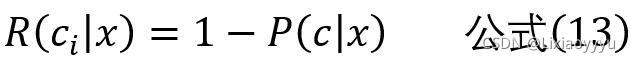
于是，最小化分类错误率的贝叶斯最优分类器为：

那分类器的意义就具体为，对样本x，选择使P（c|x）最大的类别c作为真实标记。

那么接下来，要计算后验概率P（c|x）。

而后验概率P（c|x）难以直接获得。就要使用贝叶斯定理了。

贝叶斯定理如下

如果不理解，举例进行推导

现有两个事件A，B,如何将A设为条件，那么在A发生的条件下，B（此处B表示Bi，即Bi简写成B）发生概率计算如下，

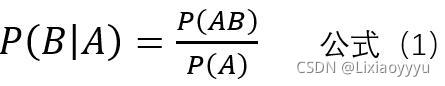
类似的，可以得如下公式，

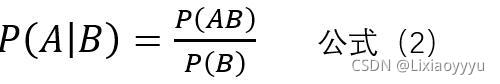
将公式（2）移项，那么易得

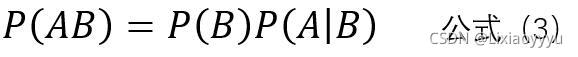
将公式（3）带入公式（1）易得
注解：当公式（6）回代时，B即为Bi

公式（4）就称之为贝叶斯定理，

由上述推导看出，贝叶斯定理揭示了如何交换条件概率的条件与结果。

此时求P(B | A）就转化为P（B)和P（A|B)。
P（A|B)是需要考虑A各属性的联合概率，对训练样本数要求巨大，不可行。

朴素贝叶斯的一大假设就在于

朴素贝叶斯假设A事件的各项属性Aj（j=1,2,3,…,m）相互独立，易得

公式（5）代入公式（4），易得
注解：此处A = ∩Ai（i=1，2，…,m)

对于对于不同的Bi，P(A）都是不变的，那么可知

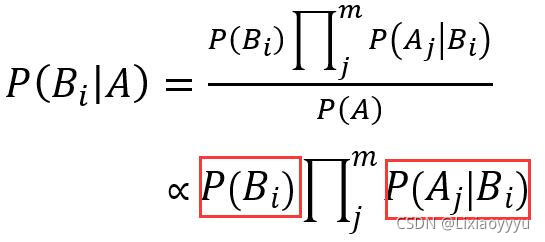
注解：特殊符号表示正比。

最终后验概率P（c|x）转化为先验概率P（c）和条件概率P（xi|c）

再回顾
贝叶斯决策论：
对样本x，选择使P（c|x）最大的类别c作为真实标记。**
表现为：如果P(c1 | x）>P(c2| x）,则分类结果为c1，否则为c2.

我们已经推导出P(Bi | A）的表达式，
P(A)是一个常数值，则P(Bi | A）正比例于红框标记的两个参数，此时只需求出这两个参数就可以进行决策。

二、极大似然估计（MLP）

极大似然估计（MLP）与极大后验概率估计（MAP）解析1

极大似然估计（MLP）与极大后验概率估计（MAP）解析2

此时，只需关注类Bi的先验概率P（Bi）和 Aj属性的条件概率P(Aj | Bi）

对于 P（Bi）和 P（ Aj | Bi）采用极大似然估计的方法取值。

朴素贝叶斯分类器的训练器的训练过程就是基于训练集D估计类先验概率P©,并为每个属性估计条件概率P(Aj | Bi）

估计公式如下：
Dc表示所有实验数据结果为Bi的个数，D为实验数据数

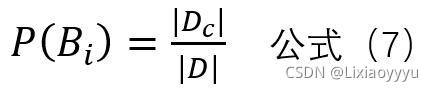
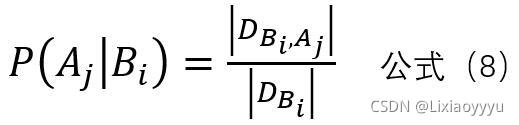
对于公式七的推导，可以点击链接2，看链接2极大似然估计的举例计算，最后 theta = X1+X2 / 2， 其中X1+X2就等于Dc，2就恰好是D, 所以可以归纳出公式七。

举例，一个女生的择偶标准如下

高矮	穷富	帅丑	嫁不嫁
高	富	帅	嫁
高	富	丑	嫁
矮	富	帅	嫁
矮	穷	帅	不嫁
高	穷	帅	不嫁
矮	穷	丑	不嫁

对于P（嫁）极大似然估计为0.5，判断是否嫁给矮、富、丑的

如果 P（ 嫁 | 矮、富、丑）> P（ 不嫁 | 矮、富、丑）则嫁，否则不嫁。

P（ 嫁 | 矮、富、丑）= 【P（嫁）* P（矮、富、丑 | 嫁 ）】/ P ( 矮、富、丑 ）
                                    = 【0.5 * P（矮 | 嫁 ）* P（ 富 | 嫁 ）* P（ 丑 | 嫁 ）】/ P ( 矮、富、丑 ）
                                    =【0.5 * 1/3 * 1 * 1/3 】 / P ( 矮、富、丑 ）
                                    = 0.5/P ( 矮、富、丑 ）

P（ 不嫁 | 矮、富、丑）= 【P（不嫁）* P（矮、富、丑 | 不嫁 ）】/ P ( 矮、富、丑 ）
                                    = 【0.5 * P（矮 | 不嫁 ）* P（ 富 | 不嫁 ）* P（ 丑 | 不嫁 ）】/ P ( 矮、富、丑 ）
此时发现不存在”富-不嫁“这个实验数据，如果以0计算，那么连乘计算的概率值为0，此时就算另外属性值为矮、丑显然会导致不嫁，结果是嫁，显然不合理。那么针对此情况就要加入平滑项，进行拉普拉斯修正。

三、拉普拉斯修正

若某个属性值在训练集中没有与某个类同时出现过，则训练后的模型会出现over-fitting现象。
为了避免其他属性携带的信息被训练集中未出现过的属性值“抹去”，在估计概率值时通常要进行”拉普拉斯修正“

令n表示训练集中出现的类别数，Ni表示A的第i个属性值可能类别数，
Dc表示所有实验数据结果为Bi的个数，D为实验数据数

则贝叶斯公式可修正为：

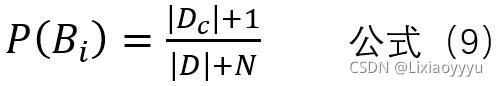
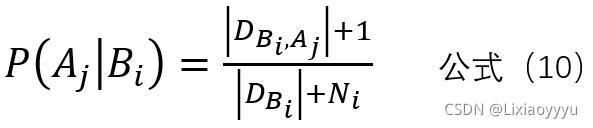
此时 P（嫁）修正为 =（3+1）/（6+2）=1/2，
P（不嫁）修正为 =（3+1）/（6+2）=1/2，可以看出非常合理。

P（ 不嫁 | 矮、富、丑）= 【P（不嫁）* P（矮、富、丑 | 不嫁 ）】/ P ( 矮、富、丑 ）
                                     = 【0.5 * P（矮 | 不嫁 ）* P（ 富 | 不嫁 ）* P（ 丑 | 不嫁 ）】/ P ( 矮、富、丑 ）
                                     = 0.5 * （2+1/3+2）*（1/3+2） * （1+1/3+2） / P ( 矮、富、丑 ）
                                     = 0.016
P（ 嫁 | 矮、富、丑）=【0.5 * （1+1/3+2） *（ 3+1/3+2） * （1+1/3+2 ）】 / P ( 矮、富、丑 ）
                                     = 0.064

P（ 嫁 | 矮、富、丑）> P（ 不嫁 | 矮、富、丑）

可认为会嫁给矮、富、丑（。。。如有冒犯，纯属巧合）

四、算法实战

使用朴素贝叶斯对电子邮件进行分类
1.收集数据：提供文本文件；
2.准备数据：将文本文件解析成词条向量；
3.分析数据：检查词条确保解析的正确性；
4.训练算法：计算先验概率和条件概率；
5.测试算法：输入测试文本，查看分类结果；
6.使用算法：构建一个完整的程序对一组文档进行分类。

1、加载数据

def load_data(folder_path):
    print("Loading dataset ...")
    loadTime = time()
    datalist = datasets.load_files(folder_path)
    #datalist是一个Bunch类，其中重要的数据项有
    #data:原始数据
    #filenames:每个文件的名称
    #target:类别标签（子目录的文件从0开始标记了索引）
    #target_names:类别标签（子目录的具体名称）
    #输出总文档数和类别数
    print("summary: {0} documents in {1} categories.".format(len(datalist.data),len(datalist.target_names)))
    #加载数据所用的时间
    print("Load data in {0}seconds".format(time() - loadTime))
    return datalist

2、文本文件解析成词条向量

生成一个所有文档中出现的不重复词的列表

def word_create(ori_data):
    #去停用词的操作
    #ori_data.data = [word for word in ori_data.data if(word not in stopwords.words('english'))]
    print("Vectorzing dataset ...")
    #建立一个集合列表
    word_dic = set([])
    #词向量的时间
    vectorTime = time()
    #词典的构造
    for doc in ori_data.data:
        #doc是byte，这里将byte转化为string
        doc = str(doc, encoding = "utf-8")
        #使用正则表达式将特殊符号去除
        doc = re.sub("[\s+\.\!\/_,$%^*(+\"\'-]+|[+——！，。？、~@#￥%……&*（）<>]+", " ", doc)
        #使用默认的空格方式将email分隔开，然后转化为小写字母，与原集合取并集
        word_dic = word_dic|set(doc.lower().split())
    #向量化的时间和词典中词的数量
    print("Vectorzing time:{0}\nThe number of word_dictionary:{1}".format(vectorTime,len(word_dic)))
    return list(word_dic)

根据词条向量，将训练文档划分成文档向量，词条出现则加1

def doc_represent(wordDic,ori_data):
    #创建一个文档数（行）*词向量（列）长度的二维数组
    doc_re = numpy.zeros((len(ori_data.data),len(wordDic)),dtype= numpy.int)
    #计数器
    count = 0
    #用来记录词向量表示时间
    representTime = time()
    for doc in ori_data.data:
        #同word_create函数，进行同样的操作
        doc = str(doc, encoding = "utf-8")
        doc = re.sub("[\s+\.\!\/_,$%^*(+\"\'-]+|[+——！，。？、~@#￥%……&*（）<>]+", " ", doc)
        for word in doc.lower().split():
            if word in wordDic:
                #将对应词向量位置置1
                doc_re[count][wordDic.index(word)] = 1
        count = count+1
    print("Represent doc time:{0}\nThe number of doc:{1}".format(representTime-time(),len(doc_re)))
    #返回表示文档的二维数组
    return doc_re

3、训练算法，计算先验概率和条件概率；

def pre_probabilty(ori_data):
    s_pre_pro = []

    #正常邮件的先验概率
    P_normal = (normal + 1.0)/(len(ori_data.data) + 2.0)
    s_pre_pro.append(P_normal)
    #垃圾邮件的先验概率
    P_spam = (spam + 1.0)/(len(ori_data.data) + 2.0)
    s_pre_pro.append(P_spam)
    #返回先验概率的列表
    return s_pre_pro

4、测试算法

#测试
def test_spam(test_repre,pre_pro,con_pro):
    email_pro = numpy.zeros((len(test_repre),2),dtype = numpy.double)
    email_judge = []
    normal_num = 0
    spam_num = 0
    for i in range(len(test_repre)):
        email_pro[i][0] = round(pre_pro[0],8)
        email_pro[i][1] = round(pre_pro[1],8)
        for j in range(len(test_repre[0])):
            if test_repre[i][j] != 0:
                email_pro[i][0] *= con_pro[0][j]
                email_pro[i][1] *= con_pro[1][j]
        if email_pro[i][0] > email_pro[i][1] :
            email_judge.append(0)
        elif email_pro[i][0] < email_pro[i][1] :
            email_judge.append(1)
        else :
            if random.random() > 0.5:
                email_judge.append(1)
            else:
                email_judge.append(0)
        if i%10 == 0:
            print(i)
    for i in range(normal_test):
        if email_judge[i] == 0:
            normal_num +=1
    for i in range(normal_test,len(test_repre)):
        if email_judge[i] == 1:
            spam_num +=1
    print("email_judge\n")
    print(email_judge)
    print("normal_num="+str(normal_num)+"\nspam_num="+str(spam_num))
    return (normal_num + spam_num)/len(test_repre)

5、使用算法

if __name__ == "__main__":
     # 训练集和测试集的路径
     train_path = "spamDataset/email/train2"
     test_path = "spamDataset/email/test2"
     train_list = load_data(train_path)
     test_list = load_data(test_path)
     # 正常邮件的数目
     normal = class_num(train_path,"pos")
     # 垃圾邮件的数目
     spam = class_num(train_path,"neg")
     #建立词汇表
     WordDictionary = word_create(train_list)
     #将训练数据进行向量表示
     docRepre = doc_represent(WordDictionary,train_list)
     #
     print(docRepre[0])
     #计算先验概率
     prePro = pre_probabilty(train_list)
     #计算条件概率
     conPro = con_probabilty(docRepre,WordDictionary)
     print("preProbablity:",prePro)
     print("conProbablity:",conPro)
     #测试数据的向量表示
     testRepre = doc_represent(WordDictionary,test_list)
     # 正常邮件的数目
     normal_test = class_num(test_path, "pos")
     # 垃圾邮件的数目
     spam_test = class_num(test_path, "neg")
     #测试数据的准确率
     test_accuracy = test_spam(testRepre,prePro,conPro)
     print ("test accuracy")
     print(test_accuracy)

根据email_judge的输出，前面0-199为正常邮件，大多数应标记为0，后200-399为垃圾邮件，大多数应标记为1，显然正确率低是因为对垃圾邮件的分类正确率低导致的。

写完了博客突然发现，一个问题，那就是为什么会想到用朴素贝叶斯来分类。
朴素贝叶斯，用定理转化求两个未知的概率，对这个两个概率最终还是用频率来估计，
那我直接用频率来估计P（ B | A )不就好了？

贻笑大方了。
这个问题就要提到生成式模型和判别式模型？