数据结构和算法之树形结构(2)

文章出处：数据结构和算法之树形结构(2)  

关注码农爱刷题，看更多技术文章！！

三、二叉查找树(接前篇)

      二叉查找树，又称二叉搜索树或二叉排序树，是在普通二叉树基础上为了实现快速查找而设计出来的一种树形结构。二叉查找树要求每个节点在树中的任意一个节点，其左子树中的每个节点的值都要小于这个节点的值，而右子树节点的值都大于这个节点的值。引进二叉查找树，是为了更高效地实现二叉树的查找和节点的增删，下图是典型的二叉查找树：

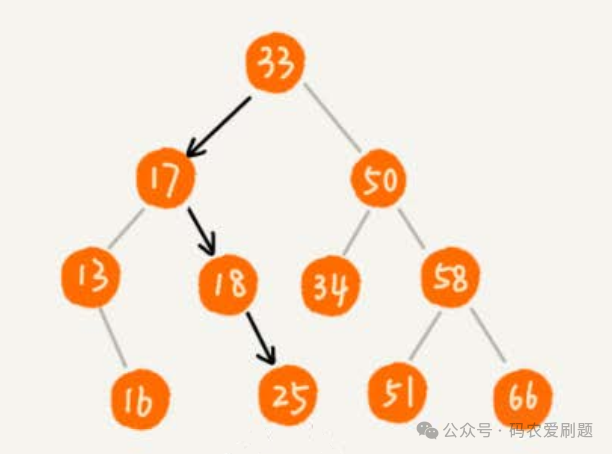
      通过中序遍历，我们很容易得到一个按值大小排序的数据序列：13,16,17,18,25,33,34,50,51,58,66。正是这样一个按值大小排序的数据序列，让二叉树节点的查找和增删变得更加高效：当查询一个节点值时，可以从根节点开始比较。如果目标值小于当前节点值，则搜索左子树；如果目标值大于当前节点值，则搜索右子树。这样理论上，每次比较都可以排除掉一半的子树，而不需要遍历整个二叉树。特别是数据集足够大并且查询频繁发生，使用二叉查找树会显著提高性能，理想的情况下二叉查找树的时间复杂度可达到 O(log n)。接下来我们详细介绍二叉查找树的各种操作的实现：

        二叉查找树的查找操作

      二叉查找树的查找其实逻辑也很简单，如前文所述：从根节点开始查找，如果目标值小于根节点值，则搜索左子树；如果目标值大于根节点值，则搜索右子树，以此类推；下面代码通过循环和递归两种方式实现了查找逻辑：

public class BinaryTreeFind {

    private Node tree; //假设已初始化树及节点

    public Node find(int data) {
        Node p = tree;
        while (p != null) {
            if (data < p.data){
              p = p.leftNode;
            } else if (data > p.data) {
              p = p.rightNode;
            } else {
              return p;
            }