数据结构-编写哈夫曼树

数据结构—哈弗曼树

（学期接近尾声，学数据结构13周了，还是好菜。）

1.哈夫曼树

树中的每个结点赋予一个数值，称为权。
从根结点到该结点之间的路径长度与该结点权的乘积为节点的带权路径长度。
所有叶子结点的带权路径长度之和最小的二叉树称为哈弗曼树。

2.哈夫曼树的构造算法

（1）根据给定的n0个权值对应构成n0棵二叉树的森林F，每棵二叉树中都只有一个带权值wi的根结点，其左右孩子为空。
（2）森林F中选取两棵结点权值最小的子树分别作为左右子树构造成一棵新的二叉树，并且新的二叉树的权值为左右子树权值之和。
（3）森林F中，用新的二叉树代替这两棵子树。
（4）重复（2）和（3），直到只剩一棵树，这棵树便是哈弗曼树。

示例：

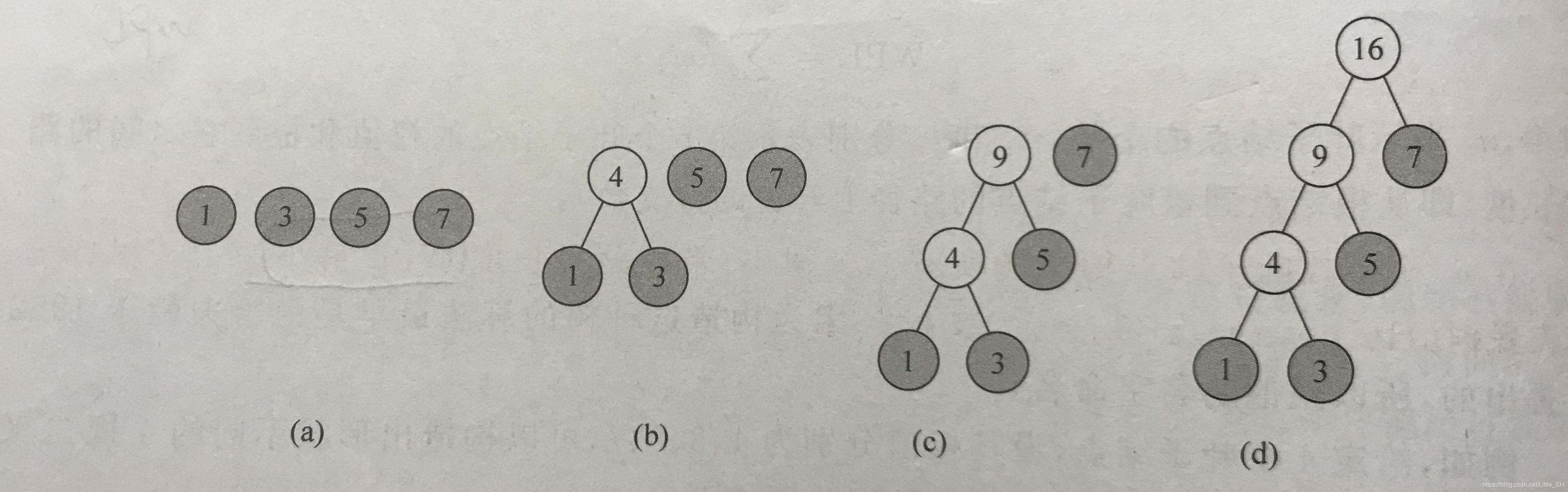
这里有个定理：对于有n0个叶子结点的哈弗曼树，共有2*n0-1个结点。

// 哈弗曼树结点类型
typedef struct
{
    char data;
    double weight;
    int parent;
    int lchild;
    int rchild;
}HTNode;

↓ht[0]~ht[n0-1]存放叶子结点，ht[n0] ~ht[2*n0-2]存放非叶子结点。

// 构造哈弗曼树
void CreateHT(HTNode ht[],int n0)
{
   
    int i,k,lnode,rnode;
    double min1