分解幂计算再加和

递推数列

- 核心:求方阵的幂
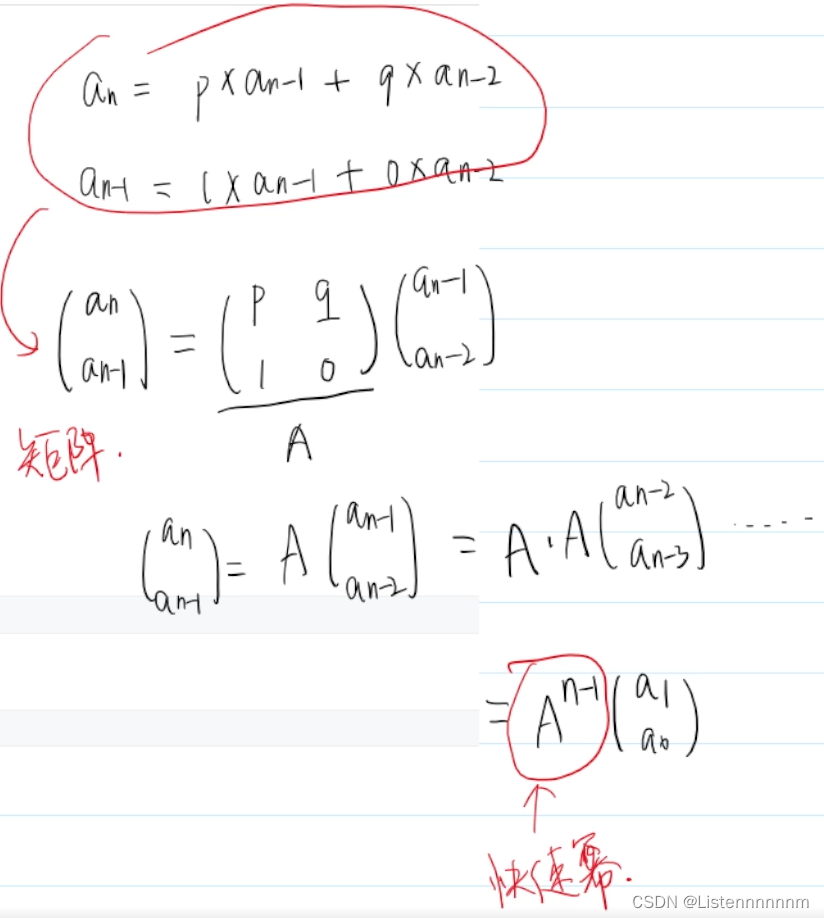
#include <iostream>
using namespace std;
void MatrixMultiply(int m1[2][2],int m2[2][2],int res[2][2]){
res[0][0] = (m1[0][0] * m2[0][0] %10000) + (m1[0][1] * m2[1][0] %10000);
res[0][0] %= 10000;
res[0][1] = (m1[0][0] * m2[0][1] %10000) + (m1[0][1] * m2[1][1] %10000);
res[0][1] %= 10000;
res[1][0] = (m1[1][0] * m2[0][0] %10000) + (m1[1][1] * m2[1][0] %10000);
res[1][0] %= 10000;
res[1][1] = (m1[1][0] * m2[0][1] %10000) + (m1[1][1] * m2[1][1] %10000);
res[1][1] %= 10000;
}
void MatrixPower(int m1[2][2],int n,int res[2][2]){
if(n == 0){
res[0][0] = 1;
res[0][1] = 0;
res[1][0] = 0;
res[1][1] = 1;
}else if(n%2==0){
int temp[2][2];
MatrixPower(m1,n/2,temp);
MatrixMultiply(temp,temp,res);
}else{
int temp1[2][2];
MatrixPower(m1,n/2,temp1);
int temp2[2][2];
MatrixMultiply(temp1,temp1,temp2);
MatrixMultiply(temp2,m1,res);
}
}
int main()
{
int matrix[2][2];
matrix[1][0] = 1;
matrix[1][1] = 0;
int a0,a1,p,q,k;
scanf("%d%d%d%d%d",&a0,&a1,&p,&q,&k);
matrix[0][0] = p;
matrix[0][1] = q;
int res[2][2];
MatrixPower(matrix,k-1,res);
printf("%d\n",(res[0][0]*a1%10000 + res[0][1]*a0%10000)%10000);
return 0;
}


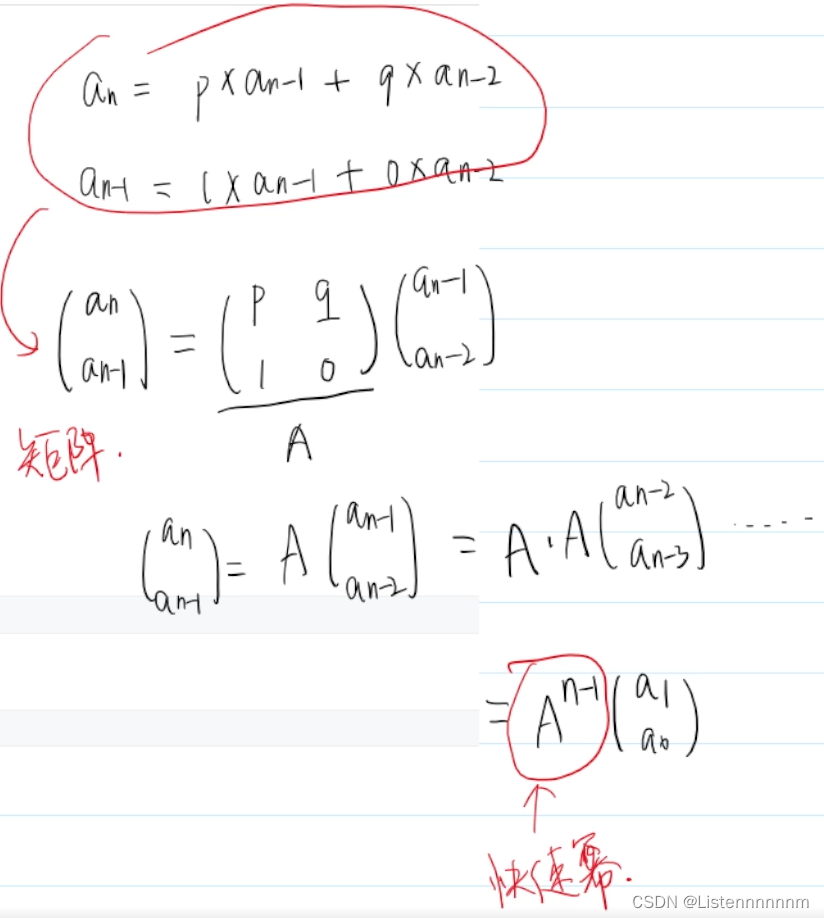








 本文介绍了如何使用C++编写核心算法,实现矩阵的幂运算,以解决递推数列中涉及矩阵乘法和求幂的问题,最终用于计算特定条件下的加和结果。
本文介绍了如何使用C++编写核心算法,实现矩阵的幂运算,以解决递推数列中涉及矩阵乘法和求幂的问题,最终用于计算特定条件下的加和结果。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










