A卷
个人解题过程思路

条件概率:P(B)>0时,P(A|B)=P(AB)/P(B)
互斥时P(AB)=0
![]() 为AB相互独立
为AB相互独立

![]() 由F(x,y)=1得a+b=1
由F(x,y)=1得a+b=1
 所以选D
所以选D

P(x<=2)=1-P(x=3)=1-(1/2)^3=7/8
i=2,A3和A4无法同时成立,D错,选C

距离为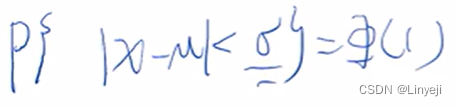 固定不变,选C
固定不变,选C

同样用条件概率:P(A|B)=P(AB)/P(B) 得:P(AB)=0.3
和U转乘n
 乘转减,为负变减数
乘转减,为负变减数
减法拆分 P(B-A)=P(B)-P(AB)
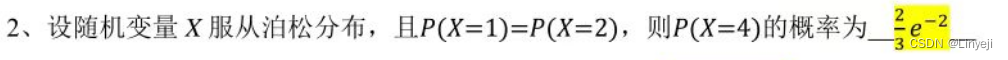
 由
由![]() 得lumda=2,然后带入就可得答案
得lumda=2,然后带入就可得答案
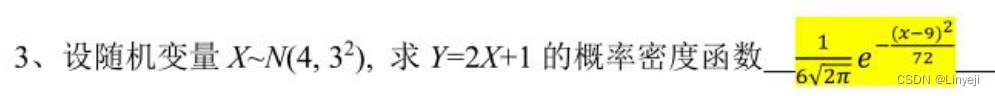
 X服从正态分布μ=E(X)=4,sigma^2=D(X)=9;
X服从正态分布μ=E(X)=4,sigma^2=D(X)=9;
Y服从正态分布μ=E(2X+1)=2*4+1=9,sigma^2=D(2X+1)=2^2*9=36

1-P{一次都没中}=0.875,1-(1-p)^3=0.875

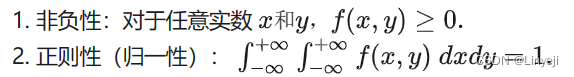 由归一性可得k*(x^3/3*y^4/4)=1 k=12
由归一性可得k*(x^3/3*y^4/4)=1 k=12

记事件A=取到第i台车床加工的零件,则P(A1)=2/3,P(A2)= 1/3,
B=取到合格品 , P(B|A1)= 0.03,P(B|A1)=0.97, P(B|A2)= 0.06,P(B|A2)=0.94

![]() 即条件概率
即条件概率

分母P(B)自然展开

整卷答案

B卷
个人解题过程思路
整卷答案





 统计与概率问题解答:条件概率、独立事件与正态分布应用
统计与概率问题解答:条件概率、独立事件与正态分布应用





 文章主要探讨了条件概率在事件独立性和互斥情况下的应用,涉及正态分布的计算,以及如何使用条件期望解决实际问题。解题过程中展示了多个实例,包括概率计算、分布性质和条件概率的计算方法。
文章主要探讨了条件概率在事件独立性和互斥情况下的应用,涉及正态分布的计算,以及如何使用条件期望解决实际问题。解题过程中展示了多个实例,包括概率计算、分布性质和条件概率的计算方法。





















 934
934

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








