第六课 算法效率的度量

本文学习自 狄泰软件学院 唐佐林老师的 数据结构课程

---

我们用算法的时间复杂度来表示算法的效率，算法的时间复杂度使用大O表示法来描述，大O表示法的工程意义可以将大O表示法作为一个算法实现或者选择的标准例如要求某个算法是时间复杂度不能超过O(n*n)

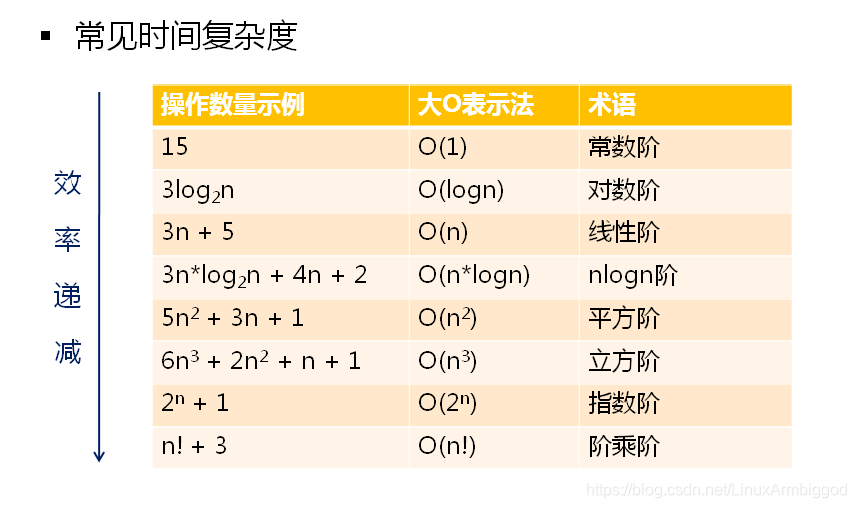
当算法的时间复杂度为O(n!)、O(2(n))、O(n(n))是，即使n很小，实际的程序运行时间也会是不可接受的。O(nnn)是分水岭，最差的算法时间复杂度是立方阶

算法的空间复杂(space Complexity)

• 定义 S(n) = S(f(n))
• n是算法的问题规模,即这个算法处理的数据元素的个数
• f(n)是空间使用函数，与n相关，即需要的内存空间
• 推导时间复杂度的方法同样适用于空间复杂度，如当算法需要的空间是常数时，空间复杂度为S(1)

空间与实践的策略

• 多数情况下，算法的时间复杂的更令人关注
• 如果有必要，可以通过增加额外空间降低时间复杂度
• 同理，也可以通过增加算法的耗时降低空间复杂度

空间换时间例子

-问题：在一个有自然数 1-1000 中的某些数组所组成的数组中，每个数字可能出现0次或多次，设计一个算法，找出出现次数最多的数字

#include <iostream>

using namespace std;

void search(int a[], int len)     // O(n)
{
    int sp[1000] = {0};//重要的初始化
    int max = 0;
    
    for(int i=0; i<len; i++)
    {
        sp[a[i] - 1]++;
    }
    
    for(int i=0; i<1000; i++)
    {
        if( max < sp[i] )
        {
            max = sp[i];
        }
    }
    
    for(int i=0; i<1000; i++)
    {
        if( max == sp[i] )
        {
            cout << i + 1 << endl;
        }
    }
}

int main(int argc, char* argv[])
{
    int a[] = {1, 1, 3, 4, 5, 6, 6, 6, 3, 3};
    
    search(a, sizeof(a)/sizeof(*a));

    return 0;
}

经典问题：当两个算法的大O表示法相同时，是否意味着两个算法的效率完全相同？
答；如果两个算法的大O表示法相同，只能够说明两个算法的效率是同一个级别的，不能够说明的这两个算法的效率完全相同

小结：

• 一般而言，工程中使用的算法，时间复杂度不超过O(n * n * n)
• 算法分析与设计时，重点考虑最坏情况下的时间复杂度
• 数据结构课程中重点关注算法的时间复杂度
• 大O表示法同样适用于算法的空间复杂度
• 空间换时间是工程开发中常用的策略