26. Remove Duplicates from Sorted Array
Given an integer array nums sorted in non-decreasing order, remove the duplicates in-place such that each unique element appears only once. The relative order of the elements should be kept the same.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the first part of the array nums. More formally, if there are k elements after removing the duplicates, then the first k elements of nums should hold the final result. It does not matter what you leave beyond the first k elements.
Return k after placing the final result in the first k slots of nums.
Do not allocate extra space for another array. You must do this by modifying the input array in-place with O(1) extra memory.
Example 1:
Input: nums = [1,1,2]
Output: 2, nums = [1,2,_]
Explanation: Your function should return k = 2, with the first two elements of nums being 1 and 2 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
Example 2:
Input: nums = [0,0,1,1,1,2,2,3,3,4]
Output: 5, nums = [0,1,2,3,4,_,_,_,_,_]
Explanation: Your function should return k = 5, with the first five elements of nums being 0, 1, 2, 3, and 4 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
# 0 <= nums.length <= 3 * 10^4
if len(nums)<2:
return len(nums)
# -100 <= nums[i] <= 100
existed_nondup_last_index=0
for i in range(1, len(nums) ):
if nums[i]!=nums[existed_nondup_last_index]:
existed_nondup_last_index +=1
nums[existed_nondup_last_index] = nums[i]
# esle: i+1
# Return k after placing the final result in the first k slots of nums.
# return the number of non-duplicates
return existed_nondup_last_index+1 27. Remove Element
Given an integer array nums and an integer val, remove all occurrences of val in nums in-place. The relative order of the elements may be changed.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the first part of the array nums. More formally, if there are k elements after removing the duplicates, then the first k elements of nums should hold the final result. It does not matter what you leave beyond the first k elements.
Return k after placing the final result in the first k slots of nums.
Do not allocate extra space for another array. You must do this by modifying the input array in-place with O(1) extra memory.
Example 1:
Input: nums = [3,2,2,3], val = 3
Output: 2, nums = [2,2,_,_]
Explanation: Your function should return k = 2, with the first two elements of nums being 2.
It does not matter what you leave beyond the returned k (hence they are underscores).
Example 2:
Input: nums = [0,1,2,2,3,0,4,2], val = 2
Output: 5, nums = [0,1,4,0,3,_,_,_]
Explanation: Your function should return k = 5, with the first five elements of nums containing 0, 0, 1, 3, and 4.
Note that the five elements can be returned in any order.
It does not matter what you leave beyond the returned k (hence they are underscores).class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
while val in nums:
nums.remove(val) # OR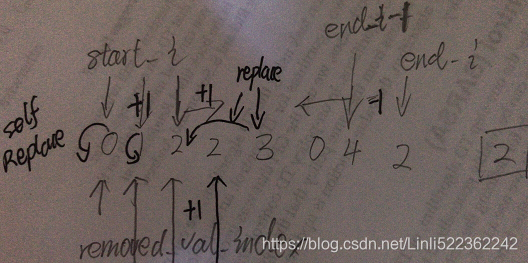
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
if len(nums)==0:
return 0
removed_val_index =0
start_i=0
end_i = len(nums)-1
while start_i <= end_i:
if nums[start_i] == val:
start_i+=1
continue
elif nums[end_i] == val:
end_i-=1
continue
else:
nums[removed_val_index] = nums[start_i]
removed_val_index+=1
start_i+=1
return removed_val_index
# removed_val_index=0
# for i in range( len(nums) ):
# if nums[i]!=val:
# nums[removed_val_index]=nums[i]
# removed_val_index +=1
# # else: continue
# return removed_val_index
# while val in nums:
# nums.remove(val)28. Implement strStr()
Implement strStr().
Return the index of the first occurrence of needle in haystack, or -1 if needle is not part of haystack.
Clarification:
What should we return when needle is an empty string? This is a great question to ask during an interview.
For the purpose of this problem, we will return 0 when needle is an empty string. This is consistent to C's strstr() and Java's indexOf().
Example 1:
Input: haystack = "hello", needle = "ll"
Output: 2
Example 2:
Input: haystack = "aaaaa", needle = "bba"
Output: -1
Example 3:
Input: haystack = "", needle = ""
Output: 0
Constraints:
0 <= haystack.length, needle.length <= 5 * 104haystackandneedleconsist of only lower-case English characters.
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
return haystack.find(needle)# OR
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
# return haystack.find(needle)
# OR
# # +1 ?
# # if len('hell')=4 - len('ll')=2, index range: 0,1 so need +1 for 'll'
for i in range( len(haystack)-len(needle)+1 ):
if haystack[ i:i+len(needle) ] == needle:
return i
return -129. Divide Two Integers
Given two integers dividend and divisor, divide two integers without using multiplication, division, and mod operator.
Return the quotient after dividing dividend by divisor.
The integer division should truncate toward zero, which means losing its fractional part. For example, truncate(8.345) = 8 and truncate(-2.7335) = -2.
Note: Assume we are dealing with an environment that could only store integers within the 32-bit signed integer range: [−231, 231 − 1]. For this problem, assume that your function returns 231 − 1 when the division result overflows.
Example 1:
Input: dividend = 10, divisor = 3
Output: 3
Explanation: 10/3 = truncate(3.33333..) = 3.
Example 2:
Input: dividend = 7, divisor = -3
Output: -2
Explanation: 7/-3 = truncate(-2.33333..) = -2.
Example 3:
Input: dividend = 0, divisor = 1
Output: 0
Example 4:
Input: dividend = 1, divisor = 1
Output: 1class Solution:
def divide(self, dividend: int, divisor: int) -> int:
# divisor != 0
if ( dividend==0 ):
return 0
# print(2**31) # 2147483647
# −2**31 = -2147483648
# if dividend = 10, divisor = 3 ==> sign=True
sign=1 if (dividend<0) == (divisor<0) else -1
dividend, divisor = abs(dividend), abs(divisor)
if dividend == divisor:
return sign
quotient=0
while dividend >=divisor: # out while loop to dividend -= divisor
deduction, doubled = divisor, 1 # 2^0 ==1
while dividend >= deduction: # inner while loop to dividend -= (divisor*=2)
dividend -= deduction
quotient += doubled
doubled<<=1 # doubled*=2
deduction<<=1 # deduction*=2
return min( max(-2147483648, quotient*sign),
2147483647
)30. Substring with Concatenation of All Words
You are given a string s and an array of strings words of the same length. Return all starting indices of substring(s) in s that is a concatenation of each word in words exactly once, in any order, and without any intervening characters.
You can return the answer in any order.
Example 1:
Input: s = "barfoothefoobarman", words = ["foo","bar"]
Output: [0,9]
Explanation: Substrings starting at index 0 and 9 are "barfoo" and "foobar" respectively.
The output order does not matter, returning [9,0] is fine too.
Example 2:
Input: s = "wordgoodgoodgoodbestword", words = ["word","good","best","word"]
Output: []
Example 3:
Input: s = "barfoofoobarthefoobarman", words = ["bar","foo","the"]
Output: [6,9,12]Input:
- "foobarfoobar"
["foo","bar"]
Expected :
- [0,3,6]
Input:
- "aaaaaaaaaaaaaa"
["aa","aa"]
Expected :
- [0,1,2,3,4,5,6,7,8,9,10]
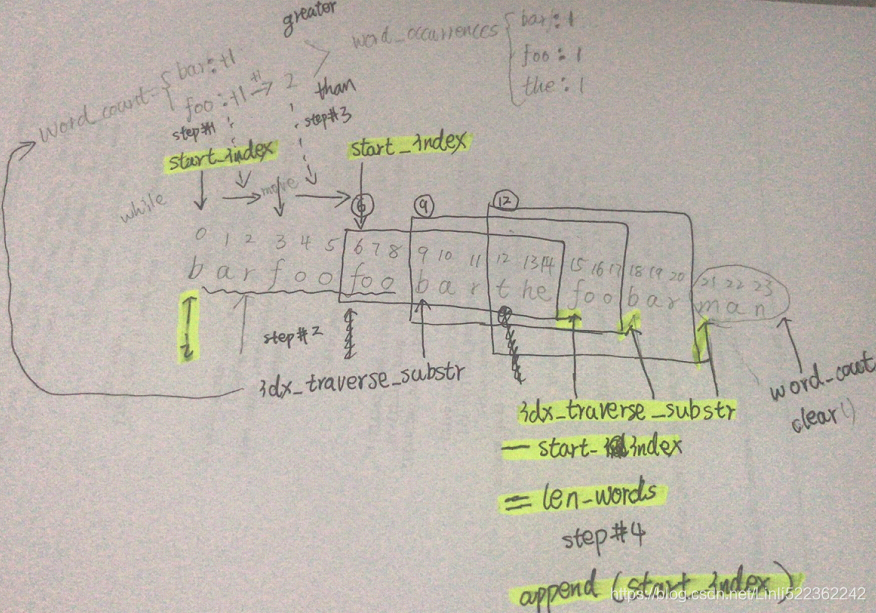
class Solution:
def findAnswer(self, start_index, len_s, len_each_word, len_words, word_occurrences, s, ans):
# I treat the substring as a window(container) including the len_words characters
# idx_traverse_substr will be used in this window
idx_traverse_substr = start_index
word_count={}
while start_index + len_words <= len_s:
consecutive_chars = s[ idx_traverse_substr : idx_traverse_substr + len_each_word ]
idx_traverse_substr += len_each_word # traverse the substring with length=len_words
if consecutive_chars not in word_occurrences:
start_index = idx_traverse_substr # next consecutive_chars on next loop, step= idx_traverse_substr += len_each_word
word_count.clear() # jump operation
continue
else: # consecutive_chars in words
if consecutive_chars in word_count:
word_count[consecutive_chars] +=1
else:
word_count[consecutive_chars] =1
# I'm looking for substring of each word's occurrence is equal to the value of word_occurrences[word]
# iterates each word in the substring (of length=len_words) for checking each word's occurrence until...
while word_count[consecutive_chars] > word_occurrences[consecutive_chars]:
word_count[ s[start_index:start_index+len_each_word] ] -= 1 # reduce the first word's occurrence
start_index += len_each_word # move the window 1 word forward, step=len_each_word
# input s: "aaaaaaaaaaaaaa"
# words: ["aa","aa"]
# idx_traverse_substr += len_each_word ==> 16;
# start_index=14
# idx_traverse_substr - start_index == len_words <==> 16-14==2 and break out when check next while loop condition
if idx_traverse_substr - start_index == len_words:
ans.append(start_index)
def findSubstring(self, s: str, words: List[str]) -> List[int]:
len_s = len(s)
len_each_word = len( words[0] )
len_words = len(words)*len_each_word
word_occurrences = {}
# s : "wordgoodgoodgoodbestword",
# words: ["word","good","best","good"]
for word in words:
if word in word_occurrences:
word_occurrences[word] +=1
else:
word_occurrences[word]=1
ans=[]
# input s: "aaaaaaaaaaaaaa"
# words: ["aa","aa"]
for i in range( min( len_each_word,
len_s-len_words+1
)
):
self.findAnswer( i, len_s, len_each_word, len_words, \
word_occurrences, s, ans )
return ans 31. Next Permutation
Implement next permutation, which rearranges numbers into the lexicographically next greater permutation of numbers.
If such an arrangement is not possible, it must rearrange it as the lowest possible order (i.e., sorted in ascending order).
The replacement must be in place and use only constant extra memory.
Example 1:
Input: nums = [1,2,3]
Output: [1,3,2]
Example 2:
Input: nums = [3,2,1]
Output: [1,2,3]
Example 3:
Input: nums = [1,1,5]
Output: [1,5,1]
Example 4:
Input: nums = [1]
Output: [1]
Constraints:
1 <= nums.length <= 100
https://www.nayuki.io/page/next-lexicographical-permutation-algorithm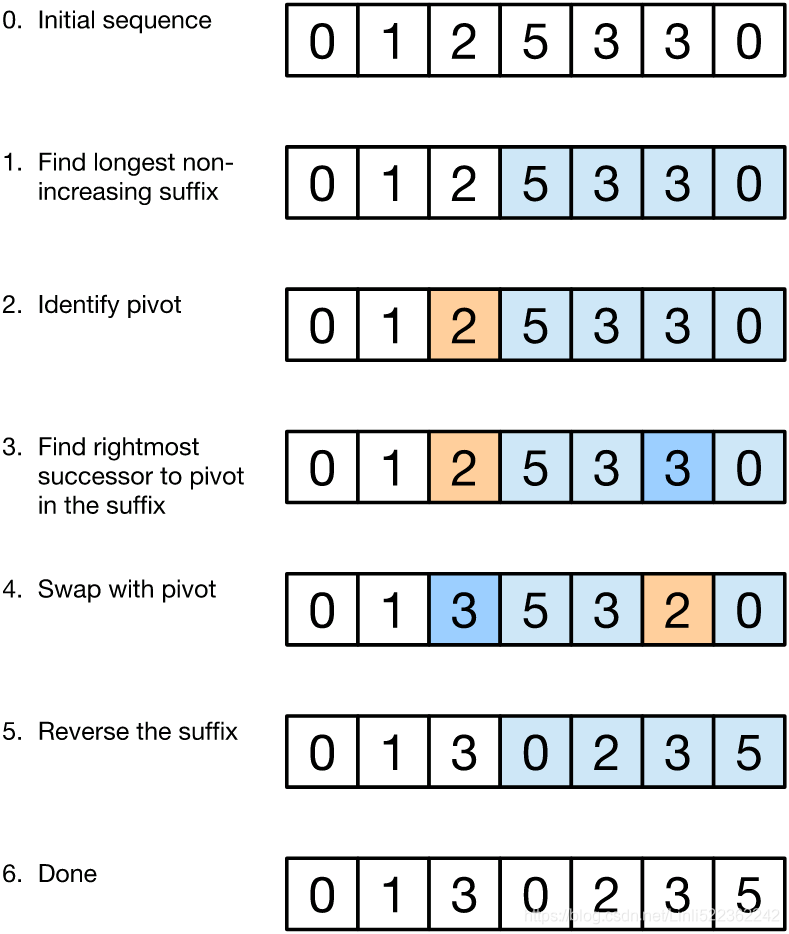
class Solution:
def nextPermutation(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
if len(nums)<2:
return
i_from_back = j_from_back = len(nums)-1
# move i_from_back from back to front to
# find the longest descending sub-list's start index
while i_from_back > 0 and nums[i_from_back-1] >= nums[i_from_back]:
i_from_back -= 1
# end of while loop,
# i_from_back is the start index of the longest descending sub-list or whole list
# or i_from_back is the index of the greatest number in the the descending sub-list
if i_from_back==0: # means the whole list of nums is in descending
nums.reverse()
return
# else i_from_back >= 1
# identify pivot : i_from_back-1
# find nums[j_from_back] > nums[i_from_back-1]
while nums[j_from_back] <= nums[i_from_back-1]:
j_from_back -= 1
# end of while loop,
# j_from_back is the index of the number > nums[i_from_back-1]
# Swap with pivot
# t = nums[j_from_back]
# nums[j_from_back] = nums[i_from_back-1]
# nums[i_from_back-1]=t
# faster and used less memory
nums[j_from_back], nums[i_from_back-1] = nums[i_from_back-1], nums[j_from_back]
# Reverse from the index i_from_back to end
left_i = i_from_back
i_from_back = len(nums)-1
while left_i < i_from_back:
# t = nums[i_from_back]
# nums[i_from_back] = nums[left_i]
# nums[left_i] = t
nums[i_from_back], nums[left_i] = nums[left_i], nums[i_from_back]
left_i +=1
i_from_back -=132. Longest Valid Parentheses
Given a string containing just the characters '(' and ')', find the length of the longest valid (well-formed) parentheses substring.
Example 1:
Input: s = "(()"
Output: 2
Explanation: The longest valid parentheses substring is "()".
Example 2:
Input: s = ")()())"
Output: 4
Explanation: The longest valid parentheses substring is "()()".
Example 3:
Input: s = ""
Output: 0
class Solution:
def longestValidParentheses(self, s: str) -> int:
if len(s) <2:
return 0
# input: "()(()()"
# expected output: 4
#i=0,1,2
# input: "(()())" #stack=[-1,0,1] ==>i=2 in s, del stack[-1] , i-stack[-1]=2-0=2
# expected output: 6
# input: ")((("
# expected output: 0
count=0
# If adjacent characters are matching parentheses, then the difference between
# their index values plus one is the number of characters
stack=[-1] # use -1 as base of stack
for i in range( len(s) ):
if s[i]=='(':
stack.append(i)
continue
else: # elif s[i]==')':
del stack[-1] #36ms faster than stack.pop() 44ms
if len(stack) ==0: # means unmatch, deleted the base of stack, then use the current index
stack.append(i)# as the base position (i-1) before next start of the next match (i, i+1)
else:
count = max( count, i-stack[-1])
# i=4
# |
# V
# s = ")()())" ==> stack=[0,]
return count OR dynamic programming 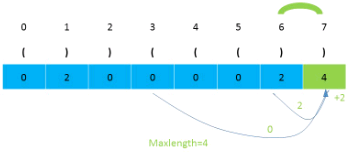
class Solution:
def longestValidParentheses(self, s: str) -> int:
if len(s) <2:
return 0
# # input: "()(()()"
# # expected output: 4
# #i=0,1,2
# # input: "(()())" #stack=[-1,0,1] ==>i=2 in s, del stack[-1] , i-stack[-1]=2-0=2
# # expected output: 6
# # input: ")((("
# # expected output: 0
# dp[5] = 6 = dp[4] + 0 + dp[-6] = 4+2+0=6
# index_0 = index_5 -1= index_5 - dp[-1] -1 = 5-4-1=0
# | dp[-1] : 4 matching chars='()()'
dp = [0] # index_3 = index_4 -1= index_4 - dp[-1] -1 = 4-0-1=3
s = ')' + s # | | dp[-1] : 0 matching chars='('
# V V dp[4]=4 = dp[3] + 2 + dp[2] = 0+2+2=4
for i in range(1, len(s), 1): # index: 0 1 2 3 4 5
if s[i] == ')' and s[ i-dp[-1]-1 ] =='(': # ( ( ) ( ) )
dp.append( dp[-1] + 2 + dp[-dp[-1]-2] ) # dp: 0 0 2 0 4 ?6 # dp[2] and dp[-6] are the dp value before '('
else:
dp.append(0)
return max(dp) 33. Search in Rotated Sorted Array
There is an integer array nums sorted in ascending order (with distinct values).
Prior to being passed to your function, nums is rotated at an unknown pivot index k (0 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].
Given the array nums after the rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.
You must write an algorithm with O(log n) runtime complexity.
Example 1:
Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4
Example 2:
Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1
Example 3:
Input: nums = [1], target = 0
Output: -1class Solution:
def search(self, nums: List[int], target: int) -> int:
try:
return nums.index( target )
except:
return -1#OR
class Solution:
def search(self, nums: List[int], target: int) -> int:
# try:
# return nums.index(target)
# except:
# return -1
# 1 <= nums.length <= 5000
if nums[0] == target:
return 0
elif len(nums)==1 and nums[0] != target:
return -1
left = 0
right = len(nums)-1
while left<=right:
middle = (left+right)//2
if nums[middle] == target:
return middle
elif nums[middle] < nums[right]: # from middle to right, nums are sorted in ascending order
if nums[middle] < target <=nums[right]: # ascending order
left = middle+1
continue
else:
right = middle-1 # target<nums[middle],left part hasn't fullly sorted, back to while condition
continue
else: # from left to middle, nums are sorted in ascending order
if nums[left] <=target <nums[middle]: # ascending order
right = middle-1
continue
else:
left = middle+1 # nums[middle]<target, right part hasn't fullly sorted, back to while condition
return -134. Find First and Last Position of Element in Sorted Array
Given an array of integers nums sorted in ascending order, find the starting and ending position of a given target value.
If target is not found in the array, return [-1, -1].
You must write an algorithm with O(log n) runtime complexity.
Example 1:
Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]
Example 2:
Input: nums = [5,7,7,8,8,10], target = 6
Output: [-1,-1]
Example 3:
Input: nums = [], target = 0
Output: [-1,-1]use the binarysearch to find the target, then push to both sides
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
# 0 <= nums.length <= 10^5
if len(nums)==0:
return [-1,-1]
if nums[0] > target or nums[-1] < target:
return [-1,-1]
left = 0
right = len(nums) -1
while left<=right:
middle=(left+right)//2
if nums[middle] == target:
left=right=middle ###
while left-1 >=0 and nums[left-1]==target:
left-=1
while right+1 <=len(nums)-1 and nums[right+1]==target:
right+=1
return [left, right] ###
elif nums[middle]<target:
left = middle+1
else: # elif target< nums[middle]:
right = middle-1
return [-1,-1] OR
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
try:
return [ nums.index(target),
len(nums)-nums[::-1].index(target)-1
]
except:
return[-1,-1]35. Search Insert Position
Given a sorted array of distinct integers and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order.
You must write an algorithm with O(log n) runtime complexity.
Example 1:
Input: nums = [1,3,5,6], target = 5
Output: 2
Example 2:
Input: nums = [1,3,5,6], target = 2
Output: 1
Example 3:
Input: nums = [1,3,5,6], target = 7
Output: 4
Example 4:
Input: nums = [1,3,5,6], target = 0
Output: 0
Example 5:
Input: nums = [1], target = 0
Output: 0![]()
One of the binary search ideas is to narrow the scope of the query. If the target is not found, it will end with the value closest to the target.
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
# 1 <= nums.length <= 10^4
if target<=nums[0]:
return 0
elif nums[-1]<target:
return len(nums)
left=0
right= len(nums)-1
while left<=right:
middle = (left+right)//2
if nums[middle] < target:
left = middle+1
else: # target <= nums[middle]
if nums[middle] == target and nums[middle-1]!=target:
return middle
else:
right = middle-1
return left # since when left==right will end of while loop36. Valid Sudoku
Determine if a 9 x 9 Sudoku board is valid. Only the filled cells need to be validated according to the following rules:
- Each row must contain the digits
1-9without repetition. - Each column must contain the digits
1-9without repetition. - Each of the nine
3 x 3sub-boxes of the grid must contain the digits1-9without repetition.
Note:
- A Sudoku board (partially filled) could be valid but is not necessarily solvable.
- Only the filled cells need to be validated according to the mentioned rules.
Example 1:

Input: board =
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
Output: true
Example 2:
Input: board =
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
Output: false
Explanation: Same as Example 1, except with the 5 in the top left corner being modified to 8. Since there are two 8's in the top left 3x3 sub-box, it is invalid.
Example 3:
[[".",".",".",".",".",".",".",".","."]
,[".",".",".",".",".",".",".",".","."]
,[".",".",".",".",".",".",".",".","."]
,[".",".",".",".",".",".",".",".","."]
,[".",".",".",".",".",".",".",".","."]
,[".",".",".",".",".",".",".",".","."]
,[".",".",".",".",".",".",".",".","."]
,[".",".",".",".",".",".",".",".","."]
,[".",".",".",".",".",".",".",".","."]]
Output: true
class Solution:
def isValidSudoku(self, board: List[List[str]]) -> bool:
# col_digits= [ [] for _ in range(9) ]
# row_digits= [ [] for _ in range(9) ]
# block_digits= [ [ [] for c in range(3) ] for r in range(3) ]
# # 0_0, 0_1, 0_2
# # 1_0, 1_1, 1_2
# # 2_0, 2_1, 2_2
# for row in range(9):
# for col in range(9):
# if board[row][col] != '.':
# if board[row][col] not in col_digits[col]:
# col_digits[col].append( board[row][col] )
# else:
# return False
# if board[row][col] not in row_digits[row]:
# row_digits[row].append( board[row][col] )
# else:
# return False
# if board[row][col] not in block_digits[row//3][col//3]:
# block_digits[row//3][col//3].append( board[row][col] )
# else:
# return False
# return True
col_digits= [ [] for _ in range(9) ] # 9 rows containing a list on each row
row_digits= [ [] for _ in range(9) ] # 9 cols containing a list on each column
block_digits= [ [ [] # sub-box
for c in range(3)
] # in 3x3 sub-boxes, there has 3 cols containing a list on each sub-box
for r in range(3)
] # there has 3 rows
# 0_0, 0_1, 0_2
# 1_0, 1_1, 1_2
# 2_0, 2_1, 2_2
for row in range(9):
for col in range(9):
if board[row][col] != '.':
if board[row][col] not in col_digits[col] and board[row][col] not in row_digits[row] and board[row][col] not in block_digits[row//3][col//3]:
col_digits[col].append( board[row][col] )
row_digits[row].append( board[row][col] )
block_digits[row//3][col//3].append( board[row][col] )
else:
return False
return TrueOR 3x3 sub-boxes, each boxe is a list
class Solution:
def isValidSudoku(self, board: List[List[str]]) -> bool:
col_digits= [ [] for _ in range(9) ] # 9 rows containing a list on each row
row_digits= [ [] for _ in range(9) ] # 9 cols containing a list on each column
block_digits= [ [] for _ in range(9) ]
# 0= (0) x3+ (0), 1= (0) x3+ (1) , 2= (0) x3+ (2)
# 3= (1) x3+ (0), 4= (1) x3+ (1) , 5= (1) x3+ (2)
# 6= (2) x3+ (0), 7= (2) x3+ (1) , 8= (2) x3+ (2)
for row in range(9):
for col in range(9):
if board[row][col] != '.':
if board[row][col] not in col_digits[col] and board[row][col] not in row_digits[row] and board[row][col] not in block_digits[row//3*3+col//3]:
col_digits[col].append( board[row][col] )
row_digits[row].append( board[row][col] )
block_digits[row//3*3+col//3].append( board[row][col] )
else:
return False
return True#OR Note: in the leetcode, should not use not in in the 2D/3D embeding list OR execute slice operation on numpy 2D-array,
Wrong:
board[row][col] not in grid[0:9][col]
board[row][col] not in grid[row//3*3:row//3*3+3,col//3*3:col//3*3+3]
class Solution:
def isValidSudoku(self, board: List[List[str]]) -> bool:
def check(row, col):
# Check if the value to be filled already exists in col
for r in range(9):
if row!=r and board[row][col] == board[r][col]:
return False
# Check if the value to be filled already exists in row
for c in range(9):
if col!=c and board[row][col] == board[row][c]:
return False
# Check whether the sub-box where the cell is located already has the value to be filled
for r in range( row//3*3, row//3*3+3 ): # uses (row//3*3, col//3*3) to locate the sub-box
for c in range( col//3*3, col//3*3+3 ):
if r!=row and c!=col and board[row][col]==board[r][c]:
return False
return True
for row in range(9):
for col in range(9):
if board[row][col] !='.':
if check(row,col):
continue
else:
return False
return True37. Sudoku Solver
Write a program to solve a Sudoku puzzle by filling the empty cells.
A sudoku solution must satisfy all of the following rules:
- Each of the digits
1-9must occur exactly once in each row. - Each of the digits
1-9must occur exactly once in each column. - Each of the digits
1-9must occur exactly once in each of the 93x3sub-boxes of the grid.
The '.' character indicates empty cells.
Example 1:

Input: board =
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
Output: [["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
Explanation: The input board is shown above and the only valid solution is shown below:
class Solution:
def check( self, r, c, board ):
# Check if the value to be filled already exists in column c
for row in range(9):
if row != r and board[row][c] == board[r][c]:
return False
# Check if the value to be filled already exists in row r
for col in range(9):
if col !=c and board[r][col] == board[r][c]:
return False
# Check whether the sub-box where the cell is located already has the value to be filled
for row in range( r//3*3, r//3*3 + 3 ): # uses (r//3*3, c//3*3) to locate the sub-box
for col in range( c//3*3, c//3*3 + 3 ):
if row!=r and col!=c and board[row][col] == board[r][c]:
return False
return True
# Depth First Strategy (tree) ######
def dfs(self, board, row_col_options):
for row, col, options in row_col_options:
if board[row][col] == '.': # find empty cell
for d in options:
board[row][col] = d # pre-set
# after check, go to next cell for filling
if self.check( row, col, board ) and self.dfs( board, row_col_options ):
return True # end of dfs
board[row][col] = '.' # recover
return False
return True
def solveSudoku(self, board: List[List[str]]) -> None:
"""
Do not return anything, modify board in-place instead.
"""
# Preprocess
col_digits= [ [] for _ in range(9) ]
row_digits= [ [] for _ in range(9) ]
block_digits= [ [] for _ in range(9) ]
# 0=0x3+0, 1=0x3+1, 2=0x3+2
# 3=1x3+0, 4=1x3+1, 5=1x3+2
# 6=2x3+0, 7=2x3+1, 8=2x3+2
coordinates = []
for row in range(9):
for col in range(9):
if board[row][col] != '.':
col_digits[col].append( board[row][col] )
row_digits[row].append( board[row][col] )
block_digits[row//3*3+col//3].append( board[row][col] )
else:
coordinates.append( (row, col) )
digits=[ str(_) for _ in range(1,10) ]
ifContinue=True
while ifContinue:
ifContinue = False
for row, col in coordinates:
t = set( row_digits[row] + col_digits[col] + block_digits[row//3*3+col//3] )
options = [ d for d in digits if d not in t ] ###
if len(options)==1:
col_digits[col].append( options[0] )
row_digits[row].append( options[0] )
block_digits[ row//3*3+col//3 ].append( options[0] )
board[row][col]=options[0] # Fill
coordinates.remove( (row,col) )
ifContinue=True
row_col_options=[]
if( len(coordinates)>0 ):
for row, col in coordinates:
t = set( row_digits[row] + col_digits[col] + block_digits[row//3*3+col//3] )
options = [ d for d in digits if d not in t ]
row_col_options.append( (row,col,options) )
del col_digits
del row_digits
del block_digits
del digits
del coordinates
self.dfs(board, row_col_options)When using dfs, you can also try to update the options table, it will run faster
38. Count and Say
The count-and-say sequence is a sequence of digit strings defined by the recursive formula:
countAndSay(1) = "1"countAndSay(n)is the way you would "say" the digit string fromcountAndSay(n-1), which is then converted into a different digit string.
To determine how you "say" a digit string, split it into the minimal number of groups so that each group is a contiguous section all of the same character. Then for each group, say the number of characters, then say the character. To convert the saying into a digit string, replace the counts with a number and concatenate every saying.
For example, the saying and conversion for digit string "3322251":(Explain so fucking)

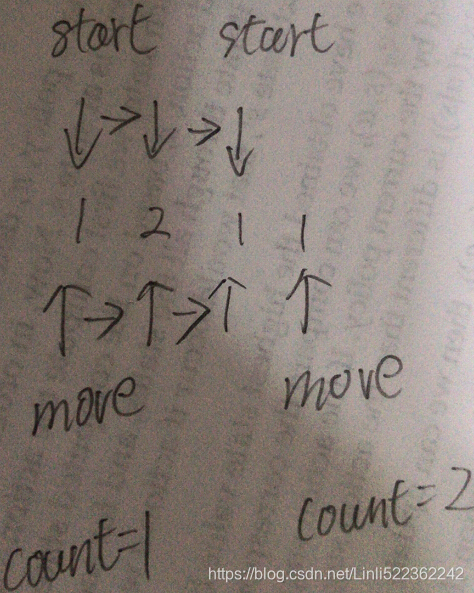
Given a positive integer n, return the nth term of the count-and-say sequence.
Example 1:
Input: n = 1
Output: "1"
Explanation: This is the base case.
Example 2:
Input: n = 4
Output: "1211"
Explanation:
countAndSay(1) = "1"
countAndSay(2) = say "1" = one 1 = "11"
countAndSay(3) = say "11" = two 1's = "21"
countAndSay(4) = say "21" = one 2 + one 1 = "12" + "11" = "1211"
class Solution:
def countAndSay(self, n: int) -> str:
# 1 <= n <= 30
# countAndSay(n=1) = "1"
# if n==1:
# return "1"
# start countAndSay(n=2) = say "1" = one 1 = "11"
previous_count_digit = "1"
for i in range(1,n):
start=0
move=0
new_count_digit=""
count=0
while move < len( previous_count_digit ):
if previous_count_digit[start] == previous_count_digit[move]:
count+=1
move+=1
continue
else: # previous_count_digit[start] != previous_count_digit[move]:
new_count_digit += str(count) + previous_count_digit[start]
start = move
count=0
new_count_digit += str(count) + previous_count_digit[start]
previous_count_digit = new_count_digit
return previous_count_digitregex
# "1" ==> re.findall( r'[1-9]', base_count_digit ) ==> ['1']
# "1" ==> re.findall( r'([\d])',base_count_digit ) ==> ['1']
# * : Match the preceding sub-expression zero or more times
# "1" ==> re.findall( r'[\d]*', base_count_digit ) ==> ['1', '']
# + : Match the preceding sub-expression one or more times.
# "1" ==> re.findall( r'[\d]+', base_count_digit ) ==> ['1']
(expressions): A related use of parenthesized subexpressions is to allow you to refer back to a subexpression later in the same regular expression. This is done by following a \ character by a digit or digits. The digits refer to the position of the parenthesized subexpression within the regular expression. For example, \1 refers back to the first subexpression, and \3 refers to the third. Note that, because subexpressions can be nested within others, it is the position of the left parenthesis that is counted. In the following regular expression,for example, the nested subexpression ([Ss]cript) is referred to as \2: /([Jj]ava([Ss]cript)?)\sis\s(fun\w*)/
# "1" ==> re.findall( r'([\d])', base_count_digit ) ==> ['1']
# "21" ==> re.findall( r'([\d]+)', base_count_digit ) ==> [('2', '1')]
# No * is added after \1, default only 1
# "1" ==> re.findall( r'( [\d] )\1', base_count_digit ) ==> [] since \1 == [\d]
# "21" ==> re.findall( r'( [\d] )\1', base_count_digit ) ==> []
# "21" ==> re.findall( r'( [\d]+ )\1', base_count_digit ) ==> []
# 1 return, () capture group, *: 0~many, +:1-many
# "1" ==> re.findall( r'( [\d] )\1*', base_count_digit ) ==> ['1']
# "11" ==> re.findall( r'( [\d] )\1*', base_count_digit ) ==> ['1']
# "21" ==> re.findall( r'( \d] )\1*', base_count_digit ) ==> ['2', '1'] # Cannot use + instead of *
# "2211" ==>re.findall( r'( [\d] )\1+', base_count_digit ) ==> ['2', '1']
# "3322251" ==>re.findall( r'( [\d] )\1*', base_count_digit ) ==>['3', '2', '5', '1']
# "3322251" ==>re.findall( r'( [\d] )\1+', base_count_digit ) ==> ['3', '2']
# 2 returns, () capture group ==> tuple
# "21" ==> re.findall( r'([\d])([\d]*)', base_count_digit ) ==> [('2', '1')]
# "1" ==> re.findall( r'( ( [\d] ) )\1*', base_count_digit ) ==> [('1', '1')]
# "1" ==> re.findall( r'( ( [\d] ) )\2*', base_count_digit ) ==> [('1', '1')]
# "21" ==>re.findall( r'( ( [\d] ) )\2*', base_count_digit ) ==>[('2', '2'), ('1', '1')]
# "3322251"==>re.findall( r'( ( [\d] ) )\2*', base_count_digit )==>[('3', '3'), ('2', '2'),('5', '5'),('1', '1')]
# "3322251"==>re.findall( r'( ( [\d] )\2*)', base_count_digit )==>[('33','3'),('222','2'),('5','5'),('1','1')]
# "11" ==> re.findall( r'( ( [\d]+ ) )\1', base_count_digit ) == > [('1', '1')]
# "21" ==> re.findall( r'( ( [\d]+ ) )\1', base_count_digit ) ==> [] since \1 == [\d]+
# "3322251" ==>re.findall( r'( ( [\d]+ ) )\1', base_count_digit ) == >[('3', '3'), ('2', '2')]
In the case of satisfying the pattern(first), Greedy mode(second)
# "11" ==> re.findall( r'( ( [\d]+ ) )\1*', base_count_digit ) ==> [('11', '11')]
# "21" ==> re.findall( r'( ( [\d]+ ) )\1', base_count_digit ) ==> [] since \1 == [\d]+
# "21" ==> re.findall( r'( ( [\d]+ ) )\1*',base_count_digit ) ==> [('21', '21')]
# "11" ==> re.findall( r'(([\d]+))\2', base_count_digit ) ==> [('1', '1')]
# "11" ==> re.findall( r'( ([\d]+) )\2*', base_count_digit ) ==> [('11', '11')]
# ([\d])* == ([\d]*) OR ([\d])+ == ([\d]+)
# "11" ==> re.findall( r'(([\d])*)\1*', base_count_digit ) ==> [('11', '1'), ('', '')]
# "11" ==> re.findall( r'(([\d])*)\2*', base_count_digit ) ==> [('11', '1'), ('', '')]
# "11" ==> re.findall( r'(([\d]*))\1*',base_count_digit ) ==> [('11', '1'), ('', '')]
# "1" ==> re.findall( r'(([\d]+))\1*',base_count_digit ) ==> [('1', '1')]
# "11" ==> re.findall( r'(([\d])*)\2+', base_count_digit ) ==> [('1', '1')]
# "11" ==> re.findall( r'(([\d])*)\2', base_count_digit ) ==> [('1', '1')]
# "11" ==> re.findall( r'(([\d])+)\1*', base_count_digit ) ==> [('11', '1')]
# "11" ==> re.findall( r'(([\d])+)\2*', base_count_digit ) ==> [('11', '1')]
class Solution:
def countAndSay(self, n: int) -> str:
import re
base_count_digit = "1"
# base_count_digit = "3322251"
# print(
# re.findall( r'(([\d])\2*)',base_count_digit )
# ) # [('33', '3'), ('222', '2'), ('5', '5'), ('1', '1')]
for _ in range(n-1): # innerCapture ==d
base_count_digit = ''.join( str( len(outerCapture) ) + d
for outerCapture, d in re.findall( r'(([\d])\2*)', # pattern
base_count_digit # string
)
)
return base_count_digit ([\d]) can be replaced with (.)
r'([\d])\1*' <==Greedy mode <== r'( ( [\d] ) \2* )'
base_count_digit = "1"
matchObj = re.match(r'([\d])\1*', base_count_digit)
print( matchObj.group(0),
matchObj.group(1)
)
'1'==> print(..) ==> 1 1
'11' ==> print(..) ==> 11 1
"33" ==> print(..) ==> 33 3
"222" ==>print(..) ==> 222 2 # 222 is from Greedy mode(longest), match pattern= r'([\d])\1*'
class Solution:
def countAndSay(self, n: int) -> str:
# # 1 <= n <= 30
# # countAndSay(n=1) = "1"
# # if n==1:
# # return "1"
# # start countAndSay(n=2) = say "1" = one 1 = "11"
# base_count_digit = "1"
# for i in range(1,n):
# start=0
# move=0
# new_count_digit=""
# count=0
# while move < len( base_count_digit ):
# if base_count_digit[start] == base_count_digit[move]:
# count+=1
# move+=1
# continue
# else: # base_count_digit[start] != base_count_digit[move]:
# new_count_digit += str(count) + base_count_digit[start]
# start = move
# count=0
# new_count_digit += str(count) + base_count_digit[start]
# base_count_digit = new_count_digit
# return base_count_digit
import re
base_count_digit = "1"
# print(# base_count_digit = "21"
# re.sub( r'([\d])\1*',
# lambda matched: str( len( matched.group(0) ) ) + matched.group(1),
# base_count_digit
# )
# ) # 1211
# base_count_digit = "3322251"
# print(
# re.findall( r'(([\d])\2*)', base_count_digit )
# ) # [('33', '3'), ('222', '2'), ('5', '5'), ('1', '1')]
for _ in range(n-1): # innerCapture ==d
# base_count_digit = ''.join( str( len(outerCapture) ) + d
# for outerCapture, d in re.findall( r'(([\d])\2*)', # pattern
# base_count_digit # string
# )
# )
# re.sub(pattern, repl, string, count=0, flags=0)
base_count_digit = re.sub( r'([\d])\1*',
lambda matched: str( len( matched.group(0) ) ) + matched.group(1),
base_count_digit
)
return base_count_digit39. Combination Sum
Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order.
The same number may be chosen from candidates an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different.
It is guaranteed that the number of unique combinations that sum up to target is less than 150 combinations for the given input.
Example 1:
Input: candidates = [2,3,6,7], target = 7
Output: [[2,2,3],[7]]
Explanation:
2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times.
7 is a candidate, and 7 = 7.
These are the only two combinations.
Example 2:
Input: candidates = [2,3,5], target = 8
Output: [[2,2,2,2],[2,3,3],[3,5]]
Example 3:
Input: candidates = [2], target = 1
Output: []
Example 4:
Input: candidates = [1], target = 1
Output: [[1]]
Example 5:
Input: candidates = [1], target = 2
Output: [[1,1]]class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
sum_list =[]
candidates.sort()
def dfs(target, start_index, comb_list):
if target==0: # target=upper_target - candidates[i]
return sum_list.append( comb_list )
# elif target !=0
for i in range( start_index, len(candidates) ):
if candidates[i] > target: # since candidates is sorted
return
else: # + since comb_list is NoneType
dfs( target-candidates[i], i, comb_list + [ candidates[i] ])
dfs( target, 0, [] )
return sum_list40. Combination Sum II
Given a collection of candidate numbers (candidates) and a target number (target), find all unique combinations in candidates where the candidate numbers sum to target.
Each number in candidates may only be used once in the combination.
Note: The solution set must not contain duplicate combinations.
Example 1:
Input: candidates = [10,1,2,7,6,1,5], target = 8
Output:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
Example 2:
Input: candidates = [2,5,2,1,2], target = 5
Output:
[
[1,2,2],
[5]
]
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
candidates.sort()
sum_list = []
def dfs( target, start_index, comb_list):
if target ==0:
#if comb_list in sum_list:
# return
#else:
return sum_list.append( comb_list )
# elif target!=0
for i in range( start_index, len(candidates) ):
# Very important here! We don't use `i > 0` because we always want
# to count the first element in this recursive step even if it is the same
# as one before. To avoid overcounting, we just ignore the duplicates
# after the first element.
if i > start_index and candidates[i] ==candidates[i-1]:
continue
elif candidates[i]>target:
return
elif i+1 <= len(candidates): # why <=? since i=len(candidates)-1 is the last item
dfs( target-candidates[i], i+1, comb_list+[ candidates[i] ] )
dfs( target, 0, [])
return sum_list41. First Missing Positive
Given an unsorted integer array nums, find the smallest missing positive integer.
You must implement an algorithm that runs in O(n) time and uses constant extra space.
Example 1:
Input: nums = [1,2,0]
Output: 3
Example 2:
Input: nums = [3,4,-1,1]
Output: 2
Example 3:
Input: nums = [7,8,9,11,12]
Output: 1class Solution:
def firstMissingPositive(self, nums: List[int]) -> int:
# 1 is True(really doesn't exist), 0 is False(exist)
true_list = [1] * len(nums) # for 0~len(nums)-1 : 1~len(nums)
for number in nums:
if number<=0: # True_list[0] will be filled with 1
continue
elif number <= len(nums): # since index+1 == number in a sorted number_list
true_list[number-1]=0 # index=number-1
# print(true_list)
for i in range( len(true_list) ):
if true_list[i]:
return i+1
# if nums=[1,2,0], we need to return len(nums), i=2, return i+1=3
# nums=[1,2,3], indice=[0,1,2], missing positive number is 4 = 3+1 =len(nums)+1
return len(nums)+1OR
class Solution:
def firstMissingPositive(self, nums: List[int]) -> int:
# 1 is True(really doesn't exist), 0 is False(exist)
nums.append(0) # for value=0 as the index is 0
n=len(nums)
for i in range( n ):
if nums[i]<0 or nums[i]>=n:
nums[i]=0
# nums=[3,4,-1,1,0] ==> nums=[3,4,0,1,0]
for i in range( len(nums) ):
nums[nums[i]%n]+=n
# 0,1, 2,3,4
# nums=[3,4,0,1,0], n=5, ==
# nums[0]==3 ==> nums[0]%n ==3,
# nums[nums[0]%n] = nums[3]==1 ==> nums[3]+=n ==> nums[3]==6
# [13 ==>nums[back 0%5]+=5 ==> nums[back 5%5]+=5, 9=4+5=[6%n]+n, 0, 6=1+5, 5=0+5]
# [13, 9, 0, 6, 5] // n = [2,1,0,1,1] ==> 0 at index=2
for i in range(1, n):
if nums[i]//n==0:
return i
return n42. Trapping Rain Water
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.
Example 1:

Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
Explanation: The above elevation map (black section) is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.
Example 2:
Input: height = [4,2,0,3,2,5]
Output: 9class Solution:
def trap(self, height: List[int]) -> int:
left_index, right_index=0, len(height)-1
left_highest, right_highest = 0, 0
water=0
while left_index < right_index:
left_highest = max( height[left_index], left_highest )
right_highest = max( height[right_index], right_highest )
if left_highest <= right_highest:
water += left_highest - height[left_index]
left_index += 1
continue
else:
water += right_highest - height[right_index]
right_index -=1
return water43. Multiply Strings
Given two non-negative integers num1 and num2 represented as strings, return the product of num1 and num2, also represented as a string.
Note: You must not use any built-in BigInteger library or convert the inputs to integer directly.
Example 1:
Input: num1 = "2", num2 = "3"
Output: "6"
Example 2:
Input: num1 = "123", num2 = "456"
Output: "56088"
class Solution:
def multiply(self, num1: str, num2: str) -> str:
# 89 * 76 = 6764
# dp = [0,0,0,0] ==> [4,6,7,6]
dp = [0]*( len(num1)+len(num2) )
for i, n1 in enumerate(num1[::-1]):
for j, n2 in enumerate(num2[::-1]):
dp[i+j] += int(n1) * int(n2) # product
dp[i+j+1] += dp[i+j] // 10 # carry
dp[i+j] %= 10
while dp[-1] == 0 and len(dp)>1:
del dp[-1]
print(ord('1'))
return ''.join( str(d) for d in dp[::-1] )44. Wildcard Matching
Given an input string (s) and a pattern (p), implement wildcard pattern matching with support for '?' and '*' where:
'?'Matches any single character.'*'Matches any sequence of characters (including the empty sequence).
The matching should cover the entire input string (not partial).
Example 1:
Input: s = "aa", p = "a"
Output: false
Explanation: "a" does not match the entire string "aa".
Example 2:
Input: s = "aa", p = "*"
Output: true
Explanation: '*' matches any sequence.
Example 3:
Input: s = "cb", p = "?a"
Output: false
Explanation: '?' matches 'c', but the second letter is 'a', which does not match 'b'.
Example 4:
Input: s = "adceb", p = "*a*b"
Output: true
Explanation: The first '*' matches the empty sequence, while the second '*' matches the substring "dce".
Example 5:
Input: s = "acdcb", p = "a*c?b"
Output: false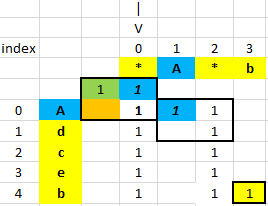 VS
VS 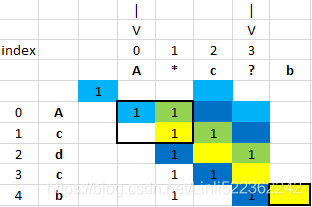
len_p = len(p)
len_s = len(s)
dp = [ [0]*(len_p+1)
for _ in range(len_s+1)
]
dp[0][0] = 1
for j in range( len_p ):
# p[j] ~ dp[:][j+1]
if p[j] == '*' and dp[0][j] ==1: # previous
dp[0][j+1] = 1
for i in range( len_s ):
for j in range( len_p ): # '?' Matches any single character.
if p[j] == s[i] or p[j]=='?': # same char
dp[i+1][j+1] = dp[i][j]
elif p[j] == '*':
dp[i+1][j+1] = dp[i+1][j] or dp[i][j+1] or dp[i][j]
return dp[len_s][len_p] ==1 https://en.wikipedia.org/wiki/Finite-state_machine
transfer

transfer = { (0,'a'): 1, (1,'*'): 1, (1,'c'): 2, (2,'?'): 3, (3,'b'): 4 }
final_state = state # state=4
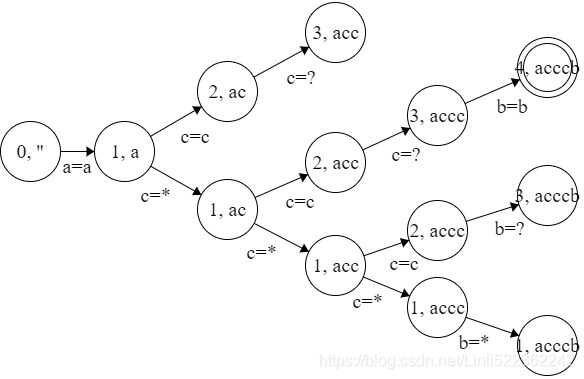
s = "acdcb"
states = {0} # # start state =0
current char: a
current state: 0 token: a next state( transfer.get( (st, token) ) ): 1 ![]()
current state: 0 token: * next state: None
current state: 0 token: ? next state: None
next_states: {1}
states: {1}
current char: c
current state: 1 token: c next state: 2 ![]()
current state: 1 token: * next state: 1 ![]()
current state: 1 token: ? next state: None
next_states: {1, 2}
states: {1, 2}
current char: d
current state: 1 token: d next state: None
current state: 2 token: d next state: None
current state: 1 token: * next state: 1
current state: 2 token: * next state: None
current state: 1 token: ? next state: None
current state: 2 token: ? next state: 3
next_states: {1, 3}
states: {1, 3}
current char: c
current state: 1 token: c next state: 2
current state: 3 token: c next state: None
current state: 1 token: * next state: 1
current state: 3 token: * next state: None
current state: 1 token: ? next state: None
current state: 3 token: ? next state: None
next_states: {1, 2}
states: {1, 2}
current char: b
current state: 1 token: b next state: None
current state: 2 token: b next state: None
current state: 1 token: * next state: 1
current state: 2 token: * next state: None
current state: 1 token: ? next state: None
current state: 2 token: ? next state: 3
next_states: {1, 3}
states: {1, 3}
return final_state in states
class Solution:
def isMatch(self, s: str, p: str) -> bool:
# https://en.wikipedia.org/wiki/Finite-state_machine
transfer = {}
state = 0
# s = "acdcb", p = "a*c?b"
for c in p:
if c == '*':
transfer[(state, c)] = state
else:
transfer[(state, c)] = state+1
state +=1
#print(transfer) #{ (0,'a'): 1, (1,'*'): 1, (1,'c'): 2, (2,'?'): 3, (3,'b'): 4 }
final_state = state # state=4
#print('final_state: ', final_state)
states = {0} # start state =0
for char in s:
# states = { transfer.get( (st, token) ) for st in states if st is not None
# for token in (char, '*', '?')
# }
#print('\ncurrent char:',char)
next_states = set()
for token in (char,'*', '?'): # check char_set()
for st in states:
next_state = transfer.get( (st, token) )
#print('current state:', st, 'token:', token, 'next state:', next_state)
if next_state!=None:
next_states.add(next_state)
#print('next_states: ',next_states)
states = next_states
#print('states: ',states)
return final_state in states45. Jump Game II
Given an array of non-negative integers nums, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Your goal is to reach the last index in the minimum number of jumps.
You can assume that you can always reach the last index.
Example 1:
Input: nums = [2,3,1,1,4]
Output: 2
Explanation: The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.
Example 2:
Input: nums = [2,3,0,1,4]
Output: 2
right index: current_farthest_postion_index
- nums[i]: maximum jump length at the position index i
- i+nums[i]: current postion index + maximum jump length at the position index i == > current_farthest_postion_index
- next_farthest_postion_index = max( i+nums[i] for i in range(left_index, current_farthest_postion_index+1) )
# Assuming the previous farthest postion index = -1
# the search range should be 0 = -1 + 1
class Solution:
def jump(self, nums: List[int]) -> int:
# 1 <= nums.length <= 10^4
# You can assume that you can always reach the last index.
if len(nums) ==1: # we don't need to check nums[0]==0
return 0 # zero step
# nums[i]: maximum jump length at the position index i
# i+nums[i]: current postion index + maximum jump length at the position index i == > current_farthest_postion_index
# Assuming the previous farthest postion index = -1
# the search range should be 0 = -1 + 1
left_index = 0 # index of the current position starting from the left
current_farthest_postion_index= nums[0] # = left_index + nums[left_index] = 0+nums[0]
steps=1
while current_farthest_postion_index < len(nums)-1:
# Breadth First Search
next_farthest_postion_index = max( i+nums[i] for i in range(left_index, current_farthest_postion_index+1) )
steps += 1
left_index = current_farthest_postion_index + 1
current_farthest_postion_index = next_farthest_postion_index
return steps46. Permutations
Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.
Example 1:
Input: nums = [1,2,3]
Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
Example 2:
Input: nums = [0,1]
Output: [[0,1],[1,0]]
Example 3:
Input: nums = [1]
Output: [[1]]class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
import itertools as it
return it.permutations(nums)OR
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
# import itertools as it
# return it.permutations(nums)
# Given an array nums of distinct integers
# DFS
permutation_list = []
def dfs( rest, permutation):
if len(rest)==0: # or # not rest:
permutation_list.append(permutation)
return
for i in range( len(rest) ):
dfs( rest[:i] + rest[i+1:], permutation + [ rest[i] ] )
# |
# V
# nums = [1,2,3]
# rest: [2,3] ==> for loop ==> [2,3] and [3,2] ==> [1,2,3],[1,3,2]
# |
# V
# nums = [1,2,3]
# rest: [1,3] ==> for loop ==> [1,3] and [3,1] ==> [2,1,3],[2,3,1]
dfs( nums, [] )
return permutation_list47. Permutations II
Given a collection of numbers, nums, that might contain duplicates(==>nums.sort()), return all possible unique permutations in any order.
Example 1:
Input: nums = [1,1,2]
Output:
[[1,1,2],
[1,2,1],
[2,1,1]]
Example 2:
Input: nums = [1,2,3]
Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
# DFS
permutation_list = []
nums.sort()### nums might contain duplicates,
def dfs( rest, permutation):
if len(rest)==0: # or # not rest:
permutation_list.append(permutation)
return
for i in range( len(rest) ):
if i > 0 and rest[i] == rest[i-1]:### note just for current rest
continue
else:
dfs( rest[:i] + rest[i+1:], permutation + [ rest[i] ] )
# |
# V
# nums = [1,1,2]
# rest: [1,2] ==> for loop(else) ==> [1,2] and [2,1] ==> [1,1,2],[1,2,1]
# | |
# V V
# nums = [1,1,2] ==> for loop(if) continue ==> nums = [1,1,2]
# rest: [1,1] ==> for loop (else) ==> [1,1] ==> [2,1,1]
# hint: for loop, i=0 ==>else
# next for loop, i=1, ==> if i > 0 and rest[i] == rest[i-1]: continue
dfs( nums, [] )
return permutation_list 48. Rotate Image
You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).
You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.
Example 1:

Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[7,4,1],[8,5,2],[9,6,3]]
print(matrix[::-1])[[7, 8, 9], [4, 5, 6], [1, 2, 3]]

print(*matrix[::-1])[7, 8, 9] [4, 5, 6] [1, 2, 3]
for i in map( list, zip(*matrix[::-1]) ):
print(i)
Example 2:

Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
Example 3:
Input: matrix = [[1]]
Output: [[1]]
Example 4:
Input: matrix = [[1,2],[3,4]]
Output: [[3,1],[4,2]]class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
matrix[:] = zip(*matrix[::-1])OR
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
# from outside to inside for an nested list
matrix[:] = [ [ row[column]
for row in matrix[::-1]
]
for column in range( len( matrix[0]) )
] # len(matrix[0] : the number of columns, but you can replace it with len(matrix) since it is a square49. Group Anagrams
Given an array of strings strs, group the anagrams together. You can return the answer in any order.
An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
Example 1:
Input: strs = ["eat","tea","tan","ate","nat","bat"] Output: [["bat"],["nat","tan"],["ate","eat","tea"]]
Example 2:
Input: strs = [""] Output: [[""]]
Example 3:
Input: strs = ["a"] Output: [["a"]]
class Solution:
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
sorted_anagrams ={}
for s in strs:
# sorted_s = sorted(s) # ==> ['a', 'e', 't']
sorted_s = ''.join( sorted(s) ) # ==> aet
if sorted_s in sorted_anagrams: # sorted_anagrams.keys()
sorted_anagrams[sorted_s].append(s)
else:
sorted_anagrams[sorted_s] = [s]
return sorted_anagrams.values()50. Pow(x, n)
Implement pow(x, n), which calculates x raised to the power n (i.e., x^n).
Example 1:
Input: x = 2.00000, n = 10 Output: 1024.00000
Example 2:
Input: x = 2.10000, n = 3 Output: 9.26100
Example 3:
Input: x = 2.00000, n = -2 Output: 0.25000 Explanation: 2-2 = 1/22 = 1/4 = 0.25
class Solution:
def myPow(self, x: float, n: int) -> float:
return x**n




 本文介绍了如何使用Python解决五个与数组、字符串相关的问题,包括去重、搜索插入位置、字符串查找等,涉及排序、动态规划和字符串匹配等技术。通过实例演示和代码实现,帮助读者掌握在O(logn)复杂度下处理问题的方法。
本文介绍了如何使用Python解决五个与数组、字符串相关的问题,包括去重、搜索插入位置、字符串查找等,涉及排序、动态规划和字符串匹配等技术。通过实例演示和代码实现,帮助读者掌握在O(logn)复杂度下处理问题的方法。

















 780
780

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










